Рисунок шестиугольника мультфильм, форма, фотография, смайлик png
Рисунок шестиугольника мультфильм, форма, фотография, смайлик pngтеги
- фотография,
- смайлик,
- мультфильм,
- форма,
- улыбка,
- пятиугольник,
- математика,
- линия,
- шестиугольник,
- геометрия,
- рисунок,
- милая форма,
- характер,
- искусство,
- png,
- прозрачный png,
- без фона,
- бесплатная загрузка
- Размер изображения
- 660x750px
- Размер файла
- 31.53KB
- MIME тип
- Image/png
изменить размер PNG
ширина(px)
высота(px)
Некоммерческое использование, DMCA Contact Us
- org/ImageObject»>
- Шестигранник Правильный многоугольник Форма Геометрия, рисунок многоугольника, угол, белый png 600x600px 8.62KB
- Треугольник Пенроуза Равносторонний треугольник Треугольник Серпинского Форма, треугольник, угол, треугольник png 706x611px 9.45KB
- шестиугольник, шестиугольная плитка, форма многоугольника, шестиугольник, угол, белый png 1000x866px 20.68KB
- Геометрическая форма Диск Прямоугольник Геометрия, смайлик квадратный, угол, текст png 816x700px 17.09KB org/ImageObject»> Octagon Обычный многоугольник, шестигранник, угол, белый png 1024x1024px 9.05KB
- Правильный многоугольник Hexagon Shape Geometry, шестиугольный, угол, белый png 2000x2000px 36.48KB
- Форма шестиугольника с шестигранной геометрией, шаблон сертификата, угол, лицо png 512x512px 1.78KB
- красное сердце, рисунок сердца, милое сердце, любовь, текст png 750x751px 83.71KB
- Шестигранник Правильная форма многоугольника, шестиугольник, угол, прямоугольник png 2000x1730px 45.31KB
- Форма шестиугольника, шестиугольник, прямоугольник, фотография png
896x1024px
116.
 27KB
27KB - Геометрический рисунок с шестигранной, шестиугольник, белый, лист png 1000x500px 24.58KB
- Геометрия Dash Shadow Face Wikia, геоментрия, разное, лицо png 1200x1200px 97.4KB
- гексагональной иллюстрации, шестигранные блоки формы фигуры, фигуры, угол, текст png 980x858px 23.1KB
- Угол Геометрическая форма Пентагон Лайн, геоматрическая, фиолетовый, прямоугольник png 800x800px 21.6KB
- Равносторонний пятиугольник Правильный многоугольник Правильный многогранник, Голден, синий, угол png 1200x1142px 29.43KB org/ImageObject»> Форма, форма, прямоугольник, геометрическая форма png 847x667px 12.63KB
- Рисование шестиугольника, шестиугольник, смайлик, многоугольник png 660x750px 31.53KB
- желтый и черный лампочки иллюстрации, математическая геометрия образования проблема формы, творческий милый мультфильм лампочки, текст, рука png 719x821px 34.47KB
- Правильный многоугольник Шестиугольник Внутренний угол Гептагон, шестигранник, угол, белый png 1024x1024px 16.14KB
- Геометрия круга формы, овальная форма, угол, белый png 586x800px 12.52KB
- Значок линии геометрии, красочные абстрактные линии геометрические квадраты, три зеленый, желтый и красный куб иллюстрации, цветной всплеск, прямоугольник png
1379x1311px
154.
 32KB
32KB - Шестигранник Форма Правильный многоугольник Геометрия, форма, синий, угол png 512x512px 14.87KB
- треугольная черная иллюстрация, треугольник геометрическая линия геометрическая форма, треугольник, угол, прямоугольник png 1280x1280px 611.17KB
- Математика Геометрия Геометрическая форма Евклидова, Геометрическая диаграмма, акварельная живопись, другие png 1938x1938px 133.79KB
- Геометрическая форма Рабочий лист Детский сад Математика, КРАСНЫЕ ФОРМЫ, лицо, треугольник png 640x640px 46.21KB
- Пчела, несущая ведро с медовой иллюстрацией, Bee Cartoon Drawing Illustration, Bee, медоносная пчела, еда png
1967x3033px
1.
 18MB
18MB - шестиугольник, шестиугольник формы компьютерные иконки символ, шестиугольник, угол, прямоугольник png 512x512px 44.63KB
- восьмиугольная золотая цифровая рамка, квадратная геометрия, геометрическая форма, формы, угол, прямоугольник png 1000x827px 54.9KB
- Geometry Dash Shadow Face Game, тире, оранжевый, люди png 1200x1200px 120.89KB
- синий и белый, геометрический рисунок треугольника на рабочем столе, треугольник, синий, угол png 988x556px 53.91KB
- Геометрия формы пятиугольника, шестиугольник, А, угол, прямоугольник png
1024x1024px
27.
 02KB
02KB - алфавит и цифры разных цветов, Элементарная математика Число Математическая запись, Математика, абстракция, стоковая фотография png 1060x796px 400.57KB
- иллюстрация черного восьмиугольника, гипотеза о сотах Шестиугольная черепица, шестиугольник, угол, белый png 1024x1024px 37.53KB
- Сота Шестиугольник, соты, угол, белый png 512x512px 10.32KB
- умножение и буквы, математика, милая маленькая математика, текст, прямоугольник png 2917x2917px 697.11KB
- Форма Шестиугольник Правильный многоугольник Геометрия, форма, угол, белый png
768x768px
16.
 22KB
22KB - Квадрат с шестигранной треугольной формы, шестиугольник, угол, прямоугольник png 958x719px 114.75KB
- Пентагон Форма Полигон Угол шестиугольника, геометрические фигуры, прямоугольник, треугольник png 1024x1024px 28.41KB
- Geometry Dash Dash до Puff 2, Шестиугольник, ГЕОМЕТРИЯ, Разное, фиолетовый png 1200x1200px 147.28KB
- Евклидова геометрия формы, форма фигуры, гексагональное цифровое искусство, угол, текст png 900x900px 141.69KB
- Гептагон Правильный многоугольник Правильний семикутник Шестиугольник, форма, угол, белый png
800x800px
18.
 62KB
62KB - Шестиугольник Геометрия Форма, форма, угол, белый png 660x598px 5.72KB
- Иллюстрация шаржа совы, милая сова, розовая птица нося иллюстрацию зеленой и белой рубашки, еда, окрашенный png 548x800px 278.42KB
- Смайлик LOL Смайлик Смех, смех, смех смайлик иллюстрация, Разное, мультфильм png 1680x1105px 1009.76KB
- Математическая иллюстрация, математическое евклидово число, дети, интересующиеся математикой, ребенок, текст png 813x926px 215.21KB
- Кривая преследования Линия Треугольник Парабола, треугольник, угол, спираль png
2308x2000px
261.
 54KB
54KB - Математический номер, математические границы, текст, прямоугольник png 2550x3300px 613.18KB
- Смайлик Смайлик Компьютер Иконки Рабочий стол, Смайлик Смайли, лицо, смайлик png 666x477px 131.29KB
- Перевод формы словаря шестиугольника многоугольника, шестиугольник, угол, белый png 512x512px 3.77KB
почему природа предпочитает шестиугольники? — T&P
При достаточной наблюдательности в живой природе легко обнаружить строгую геометрию. В особом почете оказываются гексагоны — правильные шестиугольники. Почему их так любят пчелы и архитекторы и какие у них преимущества с точки зрения физики, рассказал английский ученый и научный журналист Филип Болл. «Теории и практики» перевели отрывок из книги «Закономерности в природе: Почему живой мир выглядит так, как выглядит», опубликованный на сайте Nautilus.
Как пчелам это удается? Соты, в которых они хранят золотистый нектар, — это чудеса инженерного искусства, набор ячеек в форме призмы с правильным шестиугольником в основании. Толщина восковых стенок строго определена, ячейки немного отклоняются от горизонтали, чтобы вязкий мед не вытекал, и соты находятся в равновесии с учетом влияния магнитного поля Земли. А ведь эту конструкцию без чертежей и прогнозов строят множество пчел, которые одновременно работают и как-то координируют свои попытки сделать соты одинаковыми.
Древнегреческий философ Папп Александрийский думал, что пчелы, должно быть, наделены «геометрическим предвидением». И кто, если не Господь, мог одарить их такой мудростью? Как писал английский энтомолог Уильям Керби в середине XIX века, пчелы — «математики от Бога». Чарльз Дарвин не был в этом уверен и проводил эксперименты, чтобы установить, могут ли пчелы строить идеальные соты, используя лишь приобретенные и врожденные способности, как предполагалось в его теории эволюции. Но все же почему шестиугольник? Это чисто геометрический вопрос. Если вы хотите сложить вместе несколько одинаковых по форме и размерам ячеек таким образом, чтобы они заполняли всю плоскость, подойдут только три правильные фигуры (с равными сторонами и углами): равносторонние треугольники, квадраты и гексагоны. Если выбирать из этих вариантов, то шестиугольные соты потребуют наименьшей общей длины перегородок, в отличие от треугольников и квадратов той же площади. Поэтому в пчелиной любви к гексагонам есть смысл: на изготовление воска тратится энергия, и они стараются минимизировать расходы — точно так же, как строители пытаются сэкономить на стоимости кирпичей. К такому выводу пришли в XVIII веке, и Дарвин объявил, что соты из правильных шестиугольников «идеальны для экономии труда и воска».
Но все же почему шестиугольник? Это чисто геометрический вопрос. Если вы хотите сложить вместе несколько одинаковых по форме и размерам ячеек таким образом, чтобы они заполняли всю плоскость, подойдут только три правильные фигуры (с равными сторонами и углами): равносторонние треугольники, квадраты и гексагоны. Если выбирать из этих вариантов, то шестиугольные соты потребуют наименьшей общей длины перегородок, в отличие от треугольников и квадратов той же площади. Поэтому в пчелиной любви к гексагонам есть смысл: на изготовление воска тратится энергия, и они стараются минимизировать расходы — точно так же, как строители пытаются сэкономить на стоимости кирпичей. К такому выводу пришли в XVIII веке, и Дарвин объявил, что соты из правильных шестиугольников «идеальны для экономии труда и воска».
© Tamaki Sono / Flickr
Дарвин думал, что естественный отбор наделил пчел инстинктами для строительства восковых ячеек, у которых есть весомое преимущество: на них нужно тратить меньше времени и энергии, чем на соты других форм. И хотя кажется, что пчелы действительно обладают особыми способностями в том, что касается измерения углов и толщины стен, мнения ученых по поводу того, насколько активно насекомые их используют, расходятся, поскольку скопления шестиугольников встречаются в природе довольно часто.
И хотя кажется, что пчелы действительно обладают особыми способностями в том, что касается измерения углов и толщины стен, мнения ученых по поводу того, насколько активно насекомые их используют, расходятся, поскольку скопления шестиугольников встречаются в природе довольно часто.
Если вы подуете на пузырьки на поверхности воды, чтобы согнать их вместе, то они приобретут форму шестиугольников — или, по крайней мере, приблизятся к ней. Вы никогда не увидите скопище квадратных пузырей: если даже четыре стенки соприкоснутся, они немедленно перестроятся в конструкцию с тремя сторонами, между которыми будут примерно равные углы в 120 градусов — что-то вроде центра эмблемы «Мерседеса».
Очевидно, нет никаких организмов, которые работали бы над этими склеенными пузырями, как пчелы над сотами. Рисунок образуется исключительно благодаря законам физики. Так же очевидно, что у этих законов есть определенные предпочтения: например, склонность к трехстороннему соединению стенок пузырей. Аналогичная вещь происходит и с пеной, которая сложнее по строению. Если вы дуете через соломинку в мыльную воду и создаете «гору» пузырей в трехмерном пространстве, вы видите, что их стенки при соприкосновении всегда создают четырехсторонний союз и пересекающиеся мембраны находятся под углом около 109 градусов — это угол, который имеет непосредственное отношение к тетраэдру.
Если вы дуете через соломинку в мыльную воду и создаете «гору» пузырей в трехмерном пространстве, вы видите, что их стенки при соприкосновении всегда создают четырехсторонний союз и пересекающиеся мембраны находятся под углом около 109 градусов — это угол, который имеет непосредственное отношение к тетраэдру.
© 2day929 / Flickr
Что определяет форму пузырей и закономерности образования «развилок» мыльных стенок? Природа еще более озабочена экономией, чем пчелы. Пузыри и мыльная пленка состоят из воды (и слоя мыльных молекул), и поверхностное натяжение сжимает поверхность жидкости таким образом, чтобы она занимала наименьшую площадь. Поэтому капли дождя при падении принимают форму, близкую к сферической: у сферы наименьшая площадь поверхности по сравнению с другими фигурами того же объема. На восковом листке капли воды сжимаются в маленькие бусинки по той же причине.
Поверхностное натяжение объясняет и тот узор, который образуют пузыри или пена. Пена стремится к такой конструкции, при которой общее поверхностное натяжение будет минимальным, а значит, минимальной должна быть и площадь мыльной мембраны. Но конфигурация стенок пузырей должна быть прочной и с точки зрения механики: натяжение в разных направлениях на «перекрестке» должно быть идеально сбалансировано (по тому же принципу нужен баланс при строительстве стен собора). Трехстороннее соединение в пленке из пузырьков и четырехстороннее — в пене — комбинации, которые достигают этого баланса.
Но конфигурация стенок пузырей должна быть прочной и с точки зрения механики: натяжение в разных направлениях на «перекрестке» должно быть идеально сбалансировано (по тому же принципу нужен баланс при строительстве стен собора). Трехстороннее соединение в пленке из пузырьков и четырехстороннее — в пене — комбинации, которые достигают этого баланса.
Но тем, кто думает (а такие имеются), что соты — это просто застывшее обилие пузырей из теплого воска, трудно будет объяснить, как такие же множества шестиугольных ячеек получаются у бумажных ос, которые при строительстве используют не воск, а комки жеваных волокон древесины и стеблей, из которых они изготавливают подобие бумаги. Мало того, что поверхностное натяжение тут не играет особой роли, но к тому же ясно, что у разных видов ос разные врожденные инстинкты с точки зрения архитектурных решений: они могут значительно различаться.
Хотя геометрия стыков стенок пузырей диктуется взаимодействием механических сил, в ней бессмысленно искать намек на то, какую форму должна принять пена. Обычная пена содержит многогранные элементы различной формы и размера. Присмотритесь — и вы увидите, что их стенки не идеально прямые: они немного изогнуты. Поскольку чем меньше пузырь, тем выше в нем давление газа, стенка маленького пузыря рядом с большим будет слегка выпирать вперед. Более того, у некоторых элементов пять граней, у других — шесть, а у каких-то только четыре или всего три. При небольшой гибкости стенок все эти формы могут образовать четырехстороннее соединение, близкое по композиции к тетраэдру, что необходимо для механической устойчивости. Так что форма пузырей может изменяться. И хотя пену можно изучать с помощью правил геометрии, по своей сути она довольно хаотична.
Обычная пена содержит многогранные элементы различной формы и размера. Присмотритесь — и вы увидите, что их стенки не идеально прямые: они немного изогнуты. Поскольку чем меньше пузырь, тем выше в нем давление газа, стенка маленького пузыря рядом с большим будет слегка выпирать вперед. Более того, у некоторых элементов пять граней, у других — шесть, а у каких-то только четыре или всего три. При небольшой гибкости стенок все эти формы могут образовать четырехстороннее соединение, близкое по композиции к тетраэдру, что необходимо для механической устойчивости. Так что форма пузырей может изменяться. И хотя пену можно изучать с помощью правил геометрии, по своей сути она довольно хаотична.
Предположим, что вы могли бы сделать «идеальную» пену, в которой все пузыри одного размера. Какой тогда должна быть их идеальная форма, чтобы общая площадь стенок была наименьшей, но требование для углов на стыке выполнялось? Этот вопрос обсуждался много лет, и долгое время считалось, что идеальной формой будет четырнадцатигранник c квадратными и шестиугольными гранями. Но в 1993 году была открыта немного более экономичная, хотя и менее упорядоченная структура, состоящая из повторяющейся группы из восьми разных форм. Этот более сложный рисунок был использован в качестве вдохновения для пеноподобного дизайна водного стадиона для Олимпиады 2008 года в Пекине.
Но в 1993 году была открыта немного более экономичная, хотя и менее упорядоченная структура, состоящая из повторяющейся группы из восьми разных форм. Этот более сложный рисунок был использован в качестве вдохновения для пеноподобного дизайна водного стадиона для Олимпиады 2008 года в Пекине.
Здание Национального плавательного комплекса в Пекине © Ben McMillan
Правила, работающие для пузырей в пене, также можно отнести и к другим узорам, которые обнаруживаются в живых организмах. Не только фасеточные глаза мухи состоят из групп шестиугольных ячеек, которые напоминают группы пузырей; еще и светочувствительные клетки в каждой из этих ячеек собираются в гроздья по четыре, что опять же напоминает мыльные пузыри. Даже в случае мух-мутантов, у которых таких клеток больше, можно говорить о том, что их организация более-менее идентична поведению пузырей.
Из-за поверхностного натяжения мыльная пленка, охватывающая проволочную петлю, натянута ровно, как упругая сетка батута. Но если проволочный каркас погнут, то пленка также будет выгибаться элегантным контуром, который автоматически подсказывает вам наиболее экономичный с точки зрения использования материала способ покрытия пространства, огороженного каркасом. Таким образом, архитектор может увидеть, как построить крышу для здания со сложной архитектурой и потратить минимум стройматериалов. Как бы то ни было, дело не только в экономичности этих так называемых минимальных поверхностей, но и в их красоте и элегантности; вот почему такие архитекторы, как Фрай Отто, использовали их в качестве вдохновения для своих работ.
Но если проволочный каркас погнут, то пленка также будет выгибаться элегантным контуром, который автоматически подсказывает вам наиболее экономичный с точки зрения использования материала способ покрытия пространства, огороженного каркасом. Таким образом, архитектор может увидеть, как построить крышу для здания со сложной архитектурой и потратить минимум стройматериалов. Как бы то ни было, дело не только в экономичности этих так называемых минимальных поверхностей, но и в их красоте и элегантности; вот почему такие архитекторы, как Фрай Отто, использовали их в качестве вдохновения для своих работ.
Эти поверхности минимизируют не только площадь, но и кривизну. Чем круче изгиб, тем больше кривизна. Она может быть положительной (выпуклости) или отрицательной (углубление, впадина или прогиб). Средняя кривизна изогнутой поверхности будет нулевой, если положительная и отрицательная кривизна друг друга уравновешивают. Поэтому лист может быть весь покрыт искривлениями, а средняя кривизна окажется наименьшей. Такая минимально искривленная поверхность разрезает пространство аккуратным лабиринтом коридоров и каналов — сетью.
Такая минимально искривленная поверхность разрезает пространство аккуратным лабиринтом коридоров и каналов — сетью.
Фрай Отто, Олимпийский стадион в Мюнхене © Atelier Frei Otto Warmbronn
Это явление называют периодической минимальной поверхностью («периодическая» лишь означает, что эта структура повторяется вновь и вновь; другими словами, это постоянная последовательность). Когда такие последовательности были обнаружены в XIX веке, они казались просто математическим курьезом. Но теперь мы знаем, что природа извлекает из них пользу.
Клетки организмов различных видов, от растений до миног или крыс, обладают мембранами с подобными микроскопическими структурами. Никто не знает, зачем они нужны, но они встречаются настолько часто, что логично предположить, что они выполняют какую-то полезную функцию. Может быть, они отделяют один биохимический процесс от другого, упраздняя их взаимное влияние друг на друга. Или, возможно, они просто эффективны в качестве «рабочей поверхности», поскольку многие биохимические процессы протекают на мембранах, где могут находиться ферменты и другие активные молекулы. Каковы бы ни были функции таких лабиринтов, вам не понадобятся сложные генетические инструкции для их строительства: законы физики сделают все за вас.
Каковы бы ни были функции таких лабиринтов, вам не понадобятся сложные генетические инструкции для их строительства: законы физики сделают все за вас.
У некоторых бабочек, таких как голубянка малинная, на крыльях есть чешуйки, в которых располагается аккуратный лабиринт из жесткого материала — хитина, — сформированный в виде определенной периодической минимальной поверхности под названием гироид. Взаимодействие между неровностями на чешуйчатой поверхности крыльев приводит к тому, что волны определенной длины — то есть определенные цвета — исчезают, в то время как другие усиливают друг друга. Этот механизм влияет на окраску насекомого.
Скелет морского ежа Cidaris rugosa — пористая совокупность ячеек в форме другого вида периодической минимальной поверхности. Это экзоскелет, который расположен снаружи мягких тканей организма, защитная раковина, на которой растут кажущиеся опасными колючки из того же минерала, который входит в состав мела и мрамора. Открытая решетчатая структура указывает на то, что материал прочный, но при этом нетяжелый, — как пенометалл, который используется в авиастроительстве.
© suwich / iStock
Чтобы создать упорядоченную конструкцию из твердого неподатливого минерала, эти организмы, по всей видимости, делают макет из мягкой гнущейся мембраны и затем кристаллизуют твердое вещество внутри одной из взаимопроникающих сетей. Другие существа могут использовать минеральную пену для более сложных задач. Из нее они выстраивают конструкции-«трельяжи», которые, как зеркала, могут направлять свет за счет особенностей его отражения от рельефа. Сеть полых микроскопических каналов, напоминающих соты, в хитиновых щетинках необыкновенного морского червя (морской мыши) превращает эти волосоподобные структуры в природное оптическое волокно, которое может преломлять свет, благодаря чему цвет существа может измениться от красного до синевато-зеленого в зависимости от направления освещения. Изменение окраски помогает отпугивать хищников.
Этот принцип использования мягких тканей и мембран в качестве макета для формирования упорядоченного минерального экзоскелета широко распространен среди морских обитателей. Некоторые морские губки имеют экзоскелеты, сделанные из минеральных стержней, соединенных по принципу «паутинки» на детских площадках, и они невероятно напоминают формы, которые складываются при столкновении мыльных пузырей в пене, — и тут не может быть никаких разговоров о совпадениях, поскольку архитектуру диктует поверхностное натяжение.
Некоторые морские губки имеют экзоскелеты, сделанные из минеральных стержней, соединенных по принципу «паутинки» на детских площадках, и они невероятно напоминают формы, которые складываются при столкновении мыльных пузырей в пене, — и тут не может быть никаких разговоров о совпадениях, поскольку архитектуру диктует поверхностное натяжение.
Подобные процессы, известные как биоминерализация, дают впечатляющий результат в таких морских организмах, как лучевики и диатомеи. У некоторых из них встречаются аккуратно выстроенные экзоскелеты, состоящие из минеральных ячеек в виде гексагонов и пентагонов: их можно назвать морскими сотами. Когда немецкий естествоиспытатель (и талантливый художник) Эрнст Геккель впервые увидел эти формы в микроскоп в конце XIX века, он сделал их главным украшением своего собрания рисунков под названием «Красота форм в природе», которое сильно повлияло на художников начала XX века и до сих пор вызывает восхищение. Для Геккеля эти конструкции были доказательством фундаментальной креативности природы — предпочтение порядка и узоров, встроенное в сами законы естества. Даже если сегодня мы не разделяем эту теорию, что-то есть в этой убежденности Геккеля в том, что упорядоченность — это неудержимый импульс живого мира, и мы по праву можем считать его прекрасным.
Даже если сегодня мы не разделяем эту теорию, что-то есть в этой убежденности Геккеля в том, что упорядоченность — это неудержимый импульс живого мира, и мы по праву можем считать его прекрасным.
Как связать шестиугольник крючком + Советы и подробные фотографии
Узнайте, как связать шестиугольник крючком, используя это пошаговое руководство. Затем используйте этот базовый рисунок шестиугольника для вязания крючком, чтобы сделать шестиугольные пледы, лоскутные подушки, коврики, настенные ковры или даже одежду.
Этот пост содержит партнерские ссылки.
Базовый узор из шестиугольников крючком
Возможно, в прошлой жизни я была пчелой, потому что люблю шестиугольники! Для меня шестиугольники проходят грань между классикой, как сотовая плитка из 1920-х, но также геометрический и современный.
Мы использовали их в вязаном крючком пледе Happy Hexagons, вязаном одеяле пчеловода и вязаных свитерах, таких как кардиган для свиданий, кардиган для костра и кардиган для бранча, изображенные ниже.
Почему вам понравится вязать шестиугольники крючком!
- Портативный: Спрячьте гексы незавершенного производства в сумочке, чтобы убить время
- Гибкий мотив: Объедините свои шестиугольники в более крупный проект
- Идеальный шаблон Scrap: Используйте пряжу любой толщины, которая у вас есть
Как вязать шестиугольник крючком
Когда я впервые научилась вязать шестиугольник крючком, у меня были некоторые проблемы с пониманием других руководств, в которых не было разъяснено несколько ключевых деталей о том, как должен соединяться каждый ряд. .
Я надеюсь, что, объяснив простую математику, лежащую в основе этого основного узора шестиугольника крючком, вы точно поймете, как сделать шестиугольник любого размера.
Дополнительные уроки по вязанию шестиугольников крючком
Когда у вас будет несколько шестиугольников крючком, вам обязательно захочется проверить:
- Как связать половинку шестиугольника крючком
- Невидимый шов для соединения шестиугольников крючком
- Как соединять шестиугольники крючком на ходу (шить не нужно!) стороны и шесть углов.
 (2 столбика с накидом с каждой стороны)
(2 столбика с накидом с каждой стороны)• В каждом ряду вы будете делать столбик с накидом в каждом столбике с накидом и в каждом углу вы будете добавлять столбик с накидом, 2 воздушные петли и еще один столбик с накидом.
• Это заставляет ваш шестиугольник увеличиваться на два столбика с накидом с каждой стороны , каждый ряд.
Хотя технически существует шаблон, которому вы должны следовать для прибавлений шестигранного раунда , просто взглянув на то, что вы сделали в последнем ряду, вы поймете, что делать в следующем ряду.
Так что, надеюсь, вы не сильно запутаетесь, если вас прервут в середине раунда.
Приколи! Нажмите, чтобы прикрепить эту схему для дальнейшего использования ⇨
Что сделать из шестиугольников крючком
Как только вы освоите эту базовую выкройку шестиугольников, вы сможете сплести из них пучок и сшить из него лоскутную афганскую подушку. Вы даже можете использовать концепции этого базового шестиугольника для создания более сложных цветных мотивов шестиугольника.

В моем сердце всегда было особое место для больших проектов, требующих множества мелких повторяющихся элементов. Есть что-то действительно дзенское в том, чтобы выяснить закономерность, а затем настроить руки и разум на круиз-контроль, пока вы проворачиваете много одного и того же.
Лично мне шестиугольники нравятся больше всего!
Больше бесплатных узоров для вязания шестиугольников
Вот несколько бесплатных узоров, которые мы разработали с помощью шестиугольников.
(У нас есть много других бесплатных узоров для вязания крючком с использованием шестиугольников, и вы можете просмотреть их все здесь!)
Базовый шестиугольник Бесплатный узор для вязания крючком
Вы можете использовать любой тип пряжи для вязания шестиугольника. Просто проверьте этикетку, чтобы узнать, какой размер крючка соответствует весу вашей пряжи.
Если вы делаете что-то, что должно быть определенного размера, рекомендуется проверить калибр с помощью образца шестигранника, прежде чем делать связку.

В последнее время мне очень нравятся эти эргономичные крючки. Я не знаю, как я жил так долго без них!
Сокращения (термины США)вп — цепочка
ссн — столбик с накидом
сс — столбик без накидаРяд 1: Начните с волшебной петли. 1 вп, чтобы закрепить волшебную петлю, а затем еще 2 вп (считается как первый ссн), ссн в волшебную петлю, 2 вп, [2 ссн в волшебную петлю, 2 вп] еще 5 раз, СС до третьей вп от начала ряда до присоединиться.
(Теперь у вас есть 6 комплектов из 2 СН + 2 ВП. 2 СН станут сторонами вашего шестиугольника, а промежутки ВП станут углами.)
Ряд 2: ВП 3, СН в след. ссн, *(ссн, 2 вп, ссн) в вп-2 угла из предыдущего ряда, ссн в следующие 2 ссн; повторить от * 4 раза, (ст.с.н., 2 в.п., ссн.) в последнюю вп-2 угла, сс до третьей вп от начала раунда, чтобы присоединиться. (Каждая сторона шестиугольника теперь имеет 4 СН, разделенных пробелом в 2 вп.
 )
) Ряд 3: ВП 3, СН в следующие 2 СН, *(СН, 2 ВП, СН) в вп-2 угол от предыдущий ряд, СН в следующие 4 СН; повторить от * 4 раза, (ссн, 2 вп, ссн) в последнем вп-2 угла, ссн в оставшийся 1 стн, СС до третьей вп от начала раунда, чтобы присоединиться. (Каждая сторона шестиугольника теперь имеет 6 СН, разделенных пробелом в 2 вп.)
Ряд 4: ВП 3, СН в каждый СН в угол, *(СН, 2 ВП, СН) в угол 2 ВП из предыдущего ряда, СН в каждый СН до следующего угла ch-2; повторите от * еще 4 раза, (ст.с.н., 2 в.п., ст.с.н.) в последнюю вп-2 угла, ст.с. в оставшийся ст.с.н., сс до 3-й в.п. от начала раунда, чтобы присоединиться. (Каждая сторона шестиугольника теперь имеет 8 ст.ст.)
Ряд 5: Повтор. Ряд 4. (Каждая сторона шестиугольника теперь имеет 10 ст.ст.)
Ряд 6 и далее: Повторить Ряд 4.
Примечания к схеме вязания шестиугольников крючком
Вы можете продолжать в том же духе, чтобы сделать ваш шестиугольник настолько большим, насколько вы хотите.
 Как вы видите в этом узоре, шестиугольник увеличивается на 2 стежка с каждой стороны в каждом ряду.
Как вы видите в этом узоре, шестиугольник увеличивается на 2 стежка с каждой стороны в каждом ряду. Поскольку раунды всегда будут начинаться в одном и том же месте в середине стороны шестиугольника, каждый раунд у вас будет один дополнительный СС, чтобы закончить раунд.
В этом уроке объясняется, как соединить шестиугольники крючком невидимым швом, когда вы будете готовы сшить их вместе. Или попробуйте присоединиться к ним по ходу обучения.
Шестиугольники, связанные крючком, идеально подходят для ношения в сумочке. Начните сегодня, даже если вы не знаете, кем они станут, когда вырастут!
По этой системе набора я должен любить круглые формы, но никак не могу отойти от любимых шестиугольников. У вас есть любимая форма, которая появляется и снова появляется в вашем вязании крючком или украшении дома?
Дополнительные уроки по вязанию крючком
Изучите дополнительные советы и приемы вязания крючком с помощью этих простых руководств.

Просмотреть другие руководства по технике вязания крючком→
Бесплатные схемы вязания крючком из шестиугольников
Готовы ли вы поднять свои навыки вязания шестиугольников крючком на новый уровень? Ознакомьтесь со всеми нашими бесплатными схемами вязания крючком из шестиугольников, включая представленные ниже.
1. Кардиган Brunch // 2. Одеяло «Бабушкин цветник» // 3. Кардиган Day Date // 4. Кардиган Campfire // 5. Детский кардиган XO // 6. Одеяло Happy Hexagon
5 от 2 голосов
Закрепить для последующего чтенияКак связать шестиугольник крючком
Узнайте, как связать шестиугольник крючком, используя это пошаговое руководство. Затем используйте шестиугольники для вязания крючком, чтобы сделать шестиугольники, лоскутные подушки, коврики, настенные ковры или даже одежду.
Плотность: нет данных
Размеры: разные
Приблизительное время (зависит от уровня мастерства): 30 минут
Стоимость пряжи: $1-2
Автор: Jess Coppom )
- Крючок подходящего размера для толщины пряжи
вп – цепочка
сс – столбик с накидом
сс – столбик без накида
- 5 9002 (и дух товарищества!) в Make & Do Crochet Группа экипажа в фейсбуке.
Раунд 1: Начните с волшебной петли. 1 вп, чтобы закрепить волшебную петлю, а затем еще 2 вп (считается как первый ссн), ссн в волшебную петлю, 2 вп, [2 ссн в волшебную петлю, 2 вп] еще 5 раз, СС до третьей вп от начала ряда до присоединиться. (Теперь у вас есть 6 наборов по 2 СН + 2 ВП. 2 СН станут сторонами вашего шестиугольника, а промежутки в.п. станут углами.)
Раунд 2: 3 ВП, СН в следующий СН, *( ссн, 2 вп, ссн) в гл-2 угла из предыдущего ряда, ссн в следующие 2 ссн; повторить от * 4 раза, (ст.с.н., 2 в.п., ссн.) в последнюю вп-2 угла, сс до третьей вп от начала раунда, чтобы присоединиться. (Каждая сторона гекса теперь имеет 4 ссн, разделенных пробелом в 2 вп.
 )
)Ряд 3: 3 ВП, СН в следующие 2 СН, *(СН, 2 ВП, СН) в угол 2 вп предыдущего ряда, СН в следующие 4 СН; повторить от * 4 раза, (ссн, 2 вп, ссн) в последнем вп-2 угла, ссн в оставшийся 1 стн, СС до третьей вп от начала раунда, чтобы присоединиться. (Каждая сторона шестиугольника теперь имеет 6 ССН, разделенных пробелом в 2 ВП.)
Ряд 4: ВП 3, ССН в каждый ССН до угла, *(СН, ВП 2, ССН) в вп-2 угол от предыдущего раунд, ст.с. в каждый ст.н. до следующего угла ch-2; повторите от * еще 4 раза, (ст.с.н., 2 в.п., ст.с.н.) в последнюю вп-2 угла, ст.с. в оставшийся ст.с.н., сс до 3-й в.п. от начала раунда, чтобы присоединиться. (Каждая сторона гекса теперь имеет 8 ст.сл.)
Ряд 5: Повторить Ряд 4. (Каждая сторона шестиугольника теперь имеет 10 стежков постоянного тока.)
- ФотоФотографии 10k
- Стопка фотографийКоллекции 10k
- Группа людейПользователи 0
- 900 2 Hq фон фотографииHd фоткиHd геометрические обои Логотип Unsplash
Unsplash+
В сотрудничестве с Алексом Шупером 2 Текстурные фонышестиугольникигеометрические фигуры
Т.
 Х. Chia
Х. ChiaurbantesselationHd узор обои
Priscilla Flores
Мексика картинки и изображенияsoumaya Museumciudad de méxico
JJ Ying
Hd белые обоиФоны сайтаHd белые обои
Логотип UnsplashUnsplash+
В сотрудничестве с Alex Shuper
Unsplash+
Разблокировать
d обои на рабочий столGoogle backgrounds
Daniel Olah
Hd абстрактные обоиHd арт фоткиРадуга фото
Adrien Olichon
Hd черные обоисингапорструктура
Madison Oren
растениеПрирода фотографииHd чикаго обои
Ricky Berrelleza
buildingwalltile
Логотип UnsplashUnsplash+
В сотрудничестве с Alex Shuper
0 0 9 9 9005 Unsplash+ 05Высококачественные фоновые изображения, макросъемка. Эстетика розы
bady abbas
бизнесHd город обоиофис
обоиa3d визуализациялаймовый цвет
Hd фиолетовые обоиrendershapes
Hd 3d обоигексагон8k разрешение
Hd серые обоиd02 n250ireland
urbantesselationHd узор обои
Мексика картинки и изображенияsoumaya Museumciudad de méxico
Hd белые обоифоны сайтаHd белые обои
архитектураHd 9обои для рабочего стола
растениеПрирода фотоHd чикаго фотки
Hq фон фотомакро photo.
 rose эстетика
rose эстетика–––– –––– –––– – –––– – –––– –– – –– –––– – – –– ––– –– –––– – –.
Hd узор обоиминнеаполисmn
Текстуры фоныКомната для текстаТекстуры фоны
la défensefrancegeometry
Hq фон фотографииHd обоиHd геометрические обои
Текстуры фонашестиугольникигеометрические фигуры
2 г Абстрактные картинкиHD картинкиРадуга картинки и картинки
зданиестенаПлитка
бизнес hd город обоиофис
Похожие коллекции
мелкий узор, шестиугольник, симметрия, большая волна
1 фото · Куратор Иван ИошкинОбои с узором
423 фото · Куратор We CollectТекстура
677 фото · Куратор Julian K5 color render
5
Hd серые обоиd02 n250ireland
городская мозаикаHd узор обои
Hd белые обоиФоны сайтаHd белые обои
архитектураHd обои для рабочего столаGoogle фоны
растениеПрирода фотографииHd Чикаго обои
HD узор обоиминнеаполисmn
la défensefrancegeometry
Hq фон фотографииHd картинкиHd геометрические обои
мексика фото и изображенияsoumaya Museumciudad de méxico
9005 900 wallpapers Эстетика Hd 5Hd абстрактные картинкиHd арт фоткиРадуга фото
businessHd city wallpapersoffice
–––– –––– –––– – –––– – –––– –– – –– –––– – – –– ––– –– –––– – –.

 Найдите на Facebook.com запрос «Сделай и сделай вязание крючком».
Найдите на Facebook.com запрос «Сделай и сделай вязание крючком».Пожалуйста, не публикуйте и не делитесь этой выкройкой как своей собственной. Вы можете делать предметы на продажу по этому шаблону. Взамен дайте ссылку на эту страницу. ЗАПРЕЩАЕТСЯ использовать мои фотографии в качестве собственных фотографий для продажи.
Вы можете продолжать в том же духе, чтобы сделать ваш шестиугольник настолько большим, насколько вы хотите. Как вы видите в этом узоре, шестиугольник увеличивается на 2 стежка с каждой стороны в каждом ряду.

Поскольку раунды всегда будут начинаться в одном и том же месте в середине стороны шестиугольника, в каждом раунде у вас будет один дополнительный СС, чтобы закончить раунд.
Картинки с шестигранным узором | Скачать бесплатные изображения на Unsplash
Изображения с шестигранным узором | Скачать Free Images на Unsplashобои
узор
узор
текстура 50 90 90 90 90 909
абстракция
архитектура
соты
Логотип UnsplashUnsplash+
В сотрудничестве с Алексом Шупером
Unsplash+
Разблокировать
обои a3d renderlime color
Donny Jiang
обои Hd patternminneapolismn
–––– –––– –––– – –––– – –––– –– – –– –––– – – –– ––– –– –––– – –.
Clark Van Der Beken
Texture backgroundsroom for textTexture backgrounds
Aquarius15
la défensefrancegeometry
Marcel Straus
Hd фиолетовые обоиrendershapes 90 90 Leungson 0 Leungson 0
 27KB
27KB 32KB
32KB
 02KB
02KB 22KB
22KB 54KB
54KB (2 столбика с накидом с каждой стороны)
(2 столбика с накидом с каждой стороны)
 )
)  Как вы видите в этом узоре, шестиугольник увеличивается на 2 стежка с каждой стороны в каждом ряду.
Как вы видите в этом узоре, шестиугольник увеличивается на 2 стежка с каждой стороны в каждом ряду. 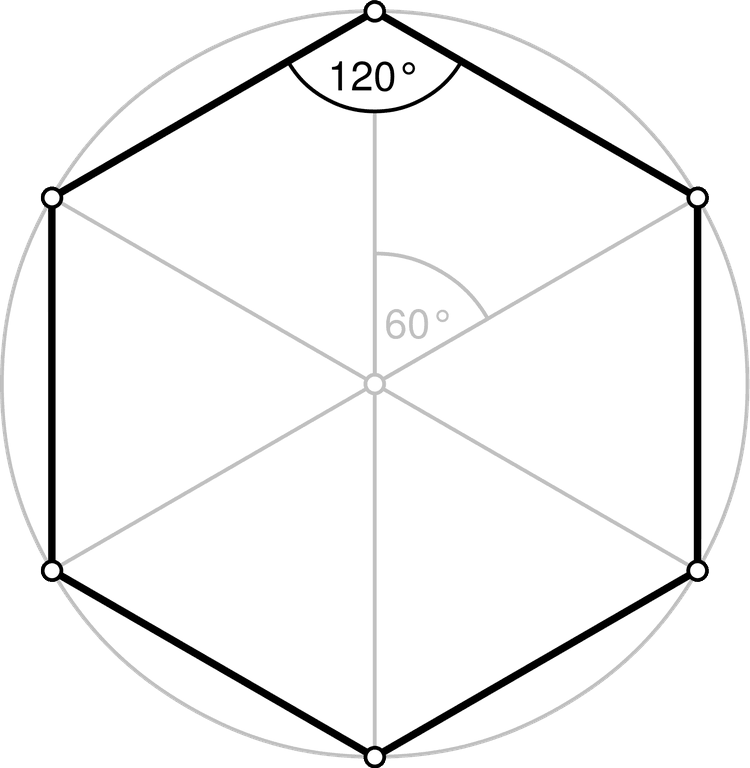
 Найдите на Facebook.com запрос «Сделай и сделай вязание крючком».
Найдите на Facebook.com запрос «Сделай и сделай вязание крючком». )
)
 Х. Chia
Х. Chia rose эстетика
rose эстетика