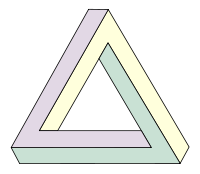
Невозможный треугольник: Невозможные и перевёрнутые фигуры. Парейдолика Треугольник пенроуза значение

Невозможные и перевёрнутые фигуры. Парейдолика Треугольник пенроуза значение

Невозможная фигура — один из видов оптических иллюзий, фигура, кажущаяся на первый взгляд проекцией обычного трёхмерного объекта,

при внимательном рассмотрении которой становятся видны противоречивые соединения элементов фигуры. Создаётся иллюзия невозможности существования такой фигуры в трёхмерном пространстве.

♦♦♦
Невозможные фигуры

Наиболее известные невозможные фигуры: невозможный треугольник, бесконечная лестница и невозможный трезубец.

Невозможный треугольник Перроуза

Иллюзия Рейтерсварда (Reutersvard, 1934)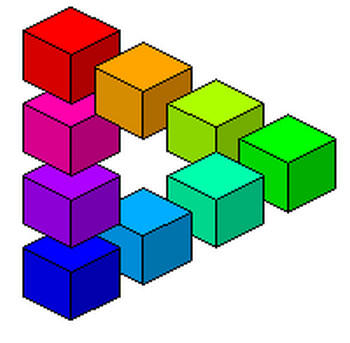

Обратите внимание также и на то, что изменение организации «фигура-фон» сделало возможным восприятие расположенной в центре «звезды».

_________

Невозможный куб Эшера

На самом деле все невозможные фигуры могут существовать в реальном мире. Так, все объекты, нарисованные на бумаге, являются проекциями трёхмерных объектов, следовательно, можно создать такой трёхмерный объект, который при проецировании на плоскость будет выглядеть невозможным. При взгляде на такой объект из определённой точки он также будет выглядеть невозможным, но при обзоре с любой другой точки эффект невозможности будет теряться.

13-метровая скульптура невозможного треугольника из алюминия была воздвигнута в 1999 году в городе Перт (Австралия). Здесь невозможный треугольник был изображен в наиболее общей форме — в виде трёх балок, соединённых друг с другом под прямыми углами.

Чёртова вилка
Среди всех невозможных фигур особое место занимает невозможный трезубец («чертова вилка»).

Если закрыть рукой пра

Что нужно знать про треугольник Пенроуза?

Невозможное все-таки возможно. И яркое подтверждение тому – невозможный треугольник Пенроуза. Открытый еще в прошлом веке, он до настоящего время часто встречается в научной литературе. И как бы это удивительно ни звучало, но его можно изготовить даже самостоятельно. И сделать это совсем несложно. Многие любители рисовать или собирать оригами уже давно смогли это сделать.

Значение треугольника Пенроуза

Существует несколько названий данной фигуры. Одни называют ее невозможным треугольником, другие – просто трибаром. Но чаще всего можно встретить определение именно «треугольник Пенроуза».

Понимают под данными определениями одну из основных невозможных фигур. Если судить по названию, то получить подобную фигуру в реальности невозможно. Но на практике было доказано, что сделать это все-таки можно. Вот только форму треугольника фигура будет принимать, если смотреть на нее с определенной точки под нужным углом. Со всех остальных сторон фигура вполне реальная. Она представляет собой три ребра куба. И изготовить подобную конструкцию легко.

История открытия

Треугольник Пенроуза был открыт в далеком 1934 году художником из Швеции Оскаром Реутерсвардом. Фигура была представлена в виде собранных вместе кубиков. В дальнейшем художника стали называть «отцом невозможных фигур».

Возможно, рисунок Реутерсварда так и остался бы малоизвестным. Но в 1954 году шведский математик Роджер Пенроуз написал статью о невозможных фигурах. Это стало вторым рождением треугольника. Правда, ученый представил его в более привычном виде. Он использовал не кубики, а балки. Три балки соединялись между собой под углом в 90 градусов. Отличие также было в том, что Реутерсвард использовал параллельную перспективу во время рисования. А Пенроуз применил перспективу линейного характера, что придало рисунку еще больше невозможности. Такой треугольник был опубликован в 1958 году в одном из британских журналов о психологии.

В 1961 году художник Мауриц Эшер (Голландия) создал одну из своих наиболее популярных литографий «Водопад». Создана она была под впечатлением, которое было вызвано статьей о невозможных фигурах.

В восьмидесятых годах прошлого столетия трибар и другие невозможные фигуры изображались на государственных почтовых марках Швеции. Продолжалось это на протяжении нескольких лет.

В конце прошлого века (а точнее в 1999 году) в Австралии была создана скульптура из алюминия, изображавшая невозможный треугольник Пенроуза. Она достигала в высоту 13 метров. Подобные скульптуры, только меньшие по размерам, встречаются и в других странах.

Невозможное в реальности

Как можно было уже догадаться, треугольник Пенроуза на самом деле не является треугольником в обычном понимании. Он представляет собой три грани куба. Но если смотреть с определенного угла, получается иллюзия треугольника за счет того, что на плоскости полностью совпадают 2 угла. Зрительно совмещается ближний от смотрящего и дальний углы.

Если быть внимательным, то можно догадаться, что трибар является не чем иным, как иллюзией. Реальный вид фигуры может выдать тень от нее. По ней видно, что на самом деле углы не соединяются. Ну и, конечно же, все становится понятно, если фигуру взять в руки.

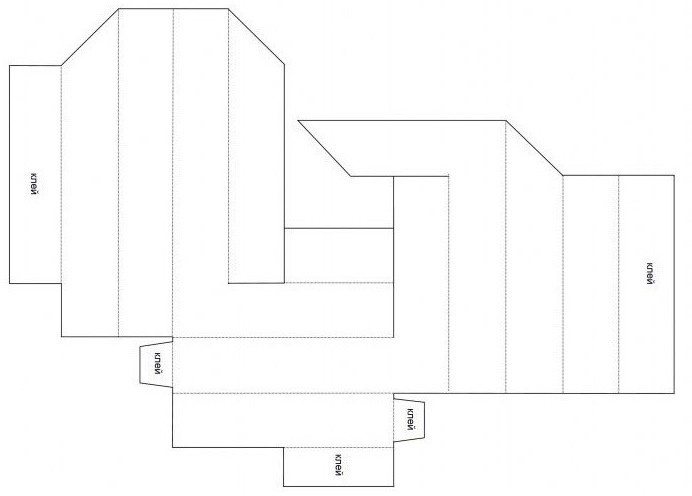
Изготовление фигуры своими руками

Треугольник Пенроуза можно собрать самостоятельно. К примеру, из бумаги или картона. И помогут в этом схемы. Их нужно всего лишь распечатать и склеить. В Интернете представлено две схемы. Одна из них немного легче, другая – посложнее, но более популярная. Обе представлены на рисунках.

Треугольник Пенроуза станет интересным изделием, которое обязательно понравится гостям. Он точно не останется незамеченным. Первым этапом для его создания является подготовка схемы. Она переносится на бумагу (картон) с помощью принтера. А далее все еще проще. Ее нужно просто вырезать по периметру. На схеме уже имеются все необходимые линии. Удобнее будет работать с более плотной бумагой. Если схема распечатана на тонкой бумаге, а хочется чего-то поплотнее, заготовка просто прикладывается на выбранный материал и вырезается по контуру. Чтобы схема не сдвигалась, ее можно прикрепить скрепками.

Далее нужно определить те линии, по которым заготовка будет сгибаться. Как правило, на схеме она представлена пунктирной линией. Сгибаем деталь. Далее определяем места, которые подлежат склеиванию. Они промазываются клеем ПВА. Деталь соединяется в единую фигуру.

Деталь можно раскрасить. А можно изначально использовать цветной картон.

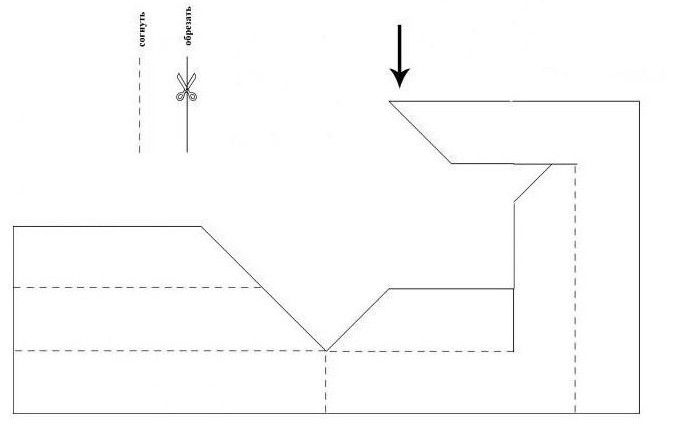
Рисуем невозможную фигуру

Треугольник Пенроуза можно также нарисовать. Для начала на листе рисуется простой квадрат. Размер его не имеет значения. С основанием на нижнюю сторону квадрата, рисуется треугольник. В его углах внутри рисуются небольшие прямоугольники. Их стороны нужно будет стереть, оставив лишь те, что являются общими с треугольником. В результате должен получиться треугольник с усеченными углами.

С левой части верхнего нижнего угла проводится прямая линия. Такая же линия, но немного короче, рисуется из левого нижнего угла. Параллельно основанию треугольника проводится линия, выходящая из правого угла. Получается второе измерение.

По принципу второго рисуется третье измерение. Только в данном случае все прямые основываются на углы фигуры не первого, а второго измерения.

Треугольник Бытия Пенроуза: scorcher_7 — LiveJournal

Многие встречались с иллюстрациями невозможных предметов, которые чаще всего можно увидеть изображенными на учебниках математики. Но немногие знают автора этих картинок. Их создатель английский физик и математик Роджер Пенроуз обладатель несчетного числа медалей, премий и титулов, внесший неоценимый вклад в развитие физики и математики.

Используя методы непериодического разбиения плоскости, он наглядно показал, как из простейших элементов можно создать великое разнообразие и в чем заключается истинная сила хаоса. Таким образом, он создал так называемую мозаику Пенроуза, позволяющую с помощью двух плиток простейшей формы замостить бесконечную плоскость никогда не повторяющимся узором. Сегодня эта мозаика очень популярна среди декораторов.

Одним из его главных достижений в физике является доказательство того, что черные дыры могут существовать как реальные физические объекты.

Прочих его достижений так же не счесть, и поскольку это не является темой нашего обсуждения, я не буду приводить их здесь все. Остановимся на невозможных объектах. Эти объекты приобрели невероятную популярность, после того как он опубликовал свою статью о них в 1958 году в Британском  журнале психологии. Самыми узнаваемыми являются Лестница Пенроуза и Треугольник Пенроуза. Оба объекта не могут существовать в реальности, но легко могут быть изображены как проекции на двухмерное пространство. При этом двухмерная проекция является полностью согласованной в соответствии с правилами проецирования двухмерных фигур. Например, если произвести геометрический анализ Лестница Пенроуза в стереометрии, то действительно получается, что она образует замкнутую поверхность, по которой можно либо вечно спускаться, либо вечно подниматься.

Треугольник Пенроуза является еще более узнаваемой фигурой, такой, что в ее честь даже воздвигнута 13-метровая скульптура в Австралии.

Естественно данная фигура выполнена по принципу оптической иллюзии, и увидеть Треугольник Пенроуза можно только с одного ракурса.

Этот треугольник затрагивает одну из самых извечных тем в философии: вопрос, где существуют такие невозможные объекты. Первым, кто попытался найти для них обитель был Платон, один из тройки древнегреческих философов связанных узами ученик-учитель, мудрость которых до сих пор оказывает влияние на наш мир. Платон, ученик Сократа, учитель Аристотеля, придумал мир чистой абстракции, место, где обитают все абстрактные вещи и понятия, в том числе и математические конструкции, место за пределами физической вселенной, где не существует времени и пространства.

Эту концепцию принято называть платоновским миром. Там существуют все понятия от простейших типа «стол», «фрукт», «дерево» до сложных наподобие «теоремы Пифагора». Платон утверждал, что только человек имеет доступ к этому миру, он в отличие, от животных глядя на предмет, видит не конкретный предмет, а его абстрактное понятие. Для животного два разных дерева, это два разных предмета, и только человек способен их обобщить понятием «дерево». А где оно существует это абстрактное дерево, которое человек видит у себя в голове, когда представляет это понятие? В качестве ответа на вопрос Платон и предложил этот мир чистой абстракции. Он утверждал, что не человек создает сущности в этом мире, а они существуют в нем изначально, и он лишь может открывать их. Так же как, например, теорема Пифагора была неоднократно открыта в древности независимыми и не знавшими друг о друге людьми.

«Идеи вечны и неизменны, а вещи изменчивы. Они являются их контурами, бледными подобиями или, всего лучше, тенями». Платон.

Концепции Платона частично нашли подтверждение в антропологии. Современные ученые считают, что первые проявления разума у человека появились лишь тогда, когда он научился абстрактно мыслить. Если попросить биолога назвать одно понятие, которое максимально характеризует жизнь, то он вынужден будет назвать: «размножение». Так же и антрополог, в ответ на вопрос какое одно понятие максимально характеризует разум, обязан сказать «абстрактное мышление».

Платон говорил, что человек способен жить в двух мирах одновременно в мире физическом и мире абстрактном. Он связывал эту особенность человека с его внутренним дуализмом, и исходя из этого выводил понятие вечной души, которая в отличии от разложимого тела способна существовать вечно в мире чистой абстракции. Однако мы не будем сильно ударятся в метафизику, и остановимся на этом в изучении идей Платона.

Пенроуз же спустя тысячелетия продолжил изучать идеи Платона о взаимодействии реального и абстрактного мира. Прежде всего, он разделил мир чистых истин Платона на два: на собственно платоновский мир и на мир ментальный. В платоновском мире Пенроуза по-прежнему живут идеальные идеи и концепции, но по-большей части он обращается только к абстрактной математике, которая существует в этом мире, поэтому мы будем называть его Математическим миром. А вот Ментальный мир – это мир, который создается в наших головах. Все что может чувствовать, думать и фантазировать человек находится именно там.

Дальше Пенроуз установил связи между тремя мирами: Математическим, Физическим и Ментальным. Прежде всего он определил, что миры происходят один из другого.

Физический мир подчиняется математическим законам, и по мере того как мы все больше узнаем о нем и заглядываем вглубь материи и пространства, то убеждаемся, что все меньше физического там остается. Самые фундаментальные разделы физики: теория относительности и квантовая механика оперируют настолько абстрактными математическими понятиями, что нам кажется, что сама реальность материи, пространства и времени в них растворяется в этой самой математике. Большой взрыв, от которого произошла наша вселенная, и вовсе содержал в себе такие энергии, что обе эти теории при его описании вообще вырождаются в чистую математику, оперирующую бесконечными значениями. Следовательно, физический мир происходит из мира математики.

Происхождение ментального мира из мира физического и вовсе кажется очевидным. Человек это физическое тело, состоящее из материи и существующее в пространстве и времени. Человек произошел на планете, которая сформировалась в космосе из пепла сгоревших звезд, которые в свою очередь зародились из газа, созданного в Большом взрыве. Но человек может думать и создавать свой собственный ментальный мир. Более того, физические условия, внешние воздействия, а так же внутренние биохимические процессы продолжают влиять на ментальный мир человека на протяжении всей его жизни.

Ну а о происхождении математического мира из мира ментального мы уже и так достаточно поговорили. Лучше привести известное выражение: «Человек это способ вселенной думать о самой себе». Здесь хочется обратить внимание на основное отличие Пенроуза от Платона. По Пенроузу математический мир именно происходит из мира ментального, а не существует независимо от него. Да, человек открывает математические теоремы, а не придумывает их. И если бы не было человека, то математические законы физики все равно бы работали, но никто не смог бы их сформулировать, никто не смог бы понять абстракцию этих законов. Математика не может существовать без того, кто ее формулирует.

Очень символично, что изображение происхождения и взаимодействия трех миров нашего бытия по Пенроузу так напоминает невозможный треугольник этого же автора.

Приглядевшись к Треугольнику Бытия повнимательней, можно заметить еще одну важную особенность, на которую указывает сам Пенроуз. Каждый из миров происходит из малой части предыдущего. И это действительно так.

В математике существует огромное количество концепций, уравнений и формул, но только часть из них воплощена в физическом мире. В основе нашего мира как считают многие физики лежит некая основополагающая система уравнений, которая пока правда не найдена. На сегодняшний день мы имеет квантовую механику со своими формулами и теорию относительности со своими, при чем часть этих формул противоречат друг другу. Однако физики верят, что наступит день, когда они смогут описать квантовую природу гравитации, и тогда они сделают из этих двух теорий одну единую, формулы которой перестанут противоречить друг другу, и тогда можно будет объявить, что математическое происхождение нашего мира полностью доказано. Но вот, что интересно… Можно ведь напридумовать множество других формул, которые так же не будут противоречить друг другу, но при этом не будут описывать нашу вселенную. Вопрос, какие вселенные тогда они будут описывать? Ответ: те, которые не существуют в реальности, но их абстракция есть в мире Математики. Большая часть этих формул порождает мертвые вселенные, нежизнеспособные, которые просуществуют меньше мгновения, или в которых не будет даже материи. Но, тем не менее, раз формулы существуют, то в этой же абстракции существуют и потенциальные возможности существования этих вселенных. Поэтому математический мир намного больше физического и происхождение последнего является лишь его малой частью.

То, что мир ментальный происходит из малой части мира физического так же очевидно. Это становится особенно очевидно, когда ночью смотришь в звездное небо и представляешь, как ничтожен человек в масштабах вселенной. Физический мир воплощает разнообразные формы материи, большинство из которых мертвы (так же как и мертвы вселенные создаваемые другими законами природы). Но, так или иначе, человек лишь крохотная часть из их разнообразия.

Так же и ментальный мир человека намного шире мира математики. Ведь, признаться, мы не так уж и часто думаем о математике. Нас обычно заботят другие вещи, и наши думы направлены зачастую никак не на изучение теорем. Мы думаем о любви, о выживании, о развлечении, о духовности. Нас интересуют культура, политика, экономика, искусство. Мы способны создавать собственные виртуальные миры, писать книги, придумывать суеверия, эзотерику или даже собственную религию. Мы можем жить в иллюзиях и заблуждениях, касательно собственной жизни и окружающего мира. Все это существует в нашем ментальном мире. Там существуют даже неправильные математики, где два плюс два равно пяти, или где число пи будет равно ровно четырем. Конечно, эти математики будут нежизнеспособны и не смогут описать наш физический мир, так же как неживая материя физического мира неспособна породить разум, так же как большинство математических формул создающих вселенные неспособные породить материю, но они существуют, по меньшей мере, в головах миллионов двоечников по всему миру.

Еще важно отметить, что само происхождение одного мира из другого по Пенроузу является непознаваемым, это трансцендентность в чистом виде. То есть по определению невозможно понять, как мир математики порождает мир физический, а тот в свою очередь порождает мир ментальный (или почему мы можем создавать свои собственные миры), и откуда в наших головах возникает логическая согласованная математика.

На этом можно было бы и закончить, но в качестве послесловия я хотел бы добавить к этому несколько своих умозаключений. Пенроуз кончено в своих размышлениях ушел намного дальше Платона. Но все же он ничего не говорит про обратную связь миров. А ведь, на самом деле, в этих мирах можно проследить не только признаки их происхождения друг из друга, но и то, как они вырождаются обратно.

Примером вырождения мира физического обратно в мир математики может служить черная дыра. Материя, пространство и время внутри черной дыры испытывают такие экстремальные условия, что все физическое внутри черной дыры превращается обратно в чистую математику, оперирующую бесконечными величинами.

Так же можно найти следы вырождения логически согласованной математики обратно в ментальный мир нелогичных суждений. Примером являются парадоксы, которыми изобилует математика, начиная со всем известного с уроков арифметики деления на ноль и заканчивая парадоксами теории множеств, такими как: парадокс Рассела, парадокс Лжеца, парадокс континуум-гипотезы. Парадокс ломает логику и заставляет нас задуматься над правильностью наших логических построений, он выталкивает нас из мира математики обратно в мир ментальный, где есть только домыслы, фантазии и предположения. Вообще, кстати, теория множеств, самая фундаментальная отрасль в математике (так же как теория относительности и квантовая механика в физике), изобилует парадоксами, и это неспроста. Математик Курт Гедель доказал так называемую Теорему о Неполноте, согласно которой любое полностью законченное замкнутое построение в математике должно содержать парадокс. Что значит замкнутое математическое построение? Когда мы что-то решаем, доказываем или выводим в математике, мы отталкиваемся от каких-то аксиом. Аксиомы – это утверждения, принимаемые без доказательств – то есть их нужно просто принять такими, какие они есть и жить с этим. Но как только мы пытаемся построить замкнутое математическое построение, в котором нет необъяснимых аксиом (или в котором аксиомы сами себя объясняют), то мы обязательно столкнемся с парадоксом, а значит, мы обязательно вывалимся из мира строгой логики в ментальный мир. Об этом и говорит Геделевская теорема о неполноте.

Давайте же попробуем понять, как в итоге должен выглядеть это треугольник Бытия. Итак:

Математический мир трансцендентально происходит из малой части ментального мира и может обратно в него вырождаться.
Физический мир трансцендентально происходит из малой части математического мира и может обратно в него вырождаться.
Ментальный мир трансцендентально происходит из малой части физического мира и может обратно в него вырождаться.

Обратите внимание о самых последних словах мы с вами ничего не говорили, но они так и просятся внутрь этой схемы, это слова о том, что «Ментальный мир тоже может вырождаться обратно в мир физический». Ведь если в мире физическом черные дыры способны обращать физику обратно в математику, если парадоксы в мире математики способны обращать строгую формальную логику обратно в ментальные домыслы, то должно существовать и нечто в мире ментальном, что воплотит его проявления в реальности. Нечто, что сделает наши ментальные образы физическими, а вымышленное – реальным. Да, конечно, человек способен воплощать свои идеи в жизнь, но только если эти идеи возможны. Однако ментальный мир намного шире, и там есть невероятные и невозможные вещи, получается и они, исходя из представленной выше схемы, должны иметь возможность как-то воплощаться в реальности.

Невозможный треугольник — это… Что такое Невозможный треугольник?



Невозможный треугольник

Треугольник Пенроуза

Треугольник Пенроуза — одна из основных невозможных фигур, известная также под названиями невозможный треугольник и трибар. Был открыт в 1938 году шведским художником Оскаром Реутерсвардом, который изобразил его в виде набора кубиков. В 1980 году этот вариант невозможного треугольника был напечатан на шведских почтовых марках.

Широкую известность эта фигура обрела после опубликования статьи о невозможных фигурах в Британском журнале психологии английским математиком Роджером Пенроузом. В этой статье невозможный треугольник был изображен в наиболее общей форме — в виде трёх балок, соединённых друг с другом под прямыми углами. Под влиянием этой статьи в 1961 голландский художник М. К. Эшер создал одну из своих знаменитых литографий «Водопад».

13-метровая скульптура невозможного треугольника из алюминия была воздвигнута в 1999 году в городе Перт (Австралия)

Ссылки

Wikimedia Foundation. 2010.

• Невозвращенец (фильм)
• Невозмутимый

Смотреть что такое «Невозможный треугольник» в других словарях:

• Треугольник Пенроуза — (в цвете) …   Википедия

• Оскар Реутерсвард — Треугольник Пенроуза Оскар Рутерсвард (принятое в русскоязычной литературе написание фамилии; правильное произношение  Рютерсверд), швед. Oscar Reutersvärd (р. 29 ноября 1915, Стокгольм, Швеция 2 февраля 2002, Лунд)  «отец невозможной фигуры»,… …   Википедия

• Оскар Рутерсвард — Треугольник Пенроуза Оскар Рутерсвард (принятое в русскоязычной литературе написание фамилии; правильное произношение  Рютерсверд), швед. Oscar Reutersvärd (р. 29 ноября 1915, Стокгольм, Швеция 2 февраля 2002, Лунд)  «отец невозможной фигуры»,… …   Википедия

• Реутерсвард — Треугольник Пенроуза Оскар Рутерсвард (принятое в русскоязычной литературе написание фамилии; правильное произношение  Рютерсверд), швед. Oscar Reutersvärd (р. 29 ноября 1915, Стокгольм, Швеция 2 февраля 2002, Лунд)  «отец невозможной фигуры»,… …   Википедия

• Реутерсвард О. — Треугольник Пенроуза Оскар Рутерсвард (принятое в русскоязычной литературе написание фамилии; правильное произношение  Рютерсверд), швед. Oscar Reutersvärd (р. 29 ноября 1915, Стокгольм, Швеция 2 февраля 2002, Лунд)  «отец невозможной фигуры»,… …   Википедия

• Реутерсвард, Оскар — Треугольник Пенроуза Оскар Рутерсвард (принятое в русскоязычной литературе написание фамилии; правильное произношение  Рютерсверд), швед. Oscar Reutersvärd (р. 29 ноября 1915, Стокгольм, Швеция 2 февраля 2002, Лунд)  «отец невозможной фигуры»,… …   Википедия

• Реутерсвард Оскар — Треугольник Пенроуза Оскар Рутерсвард (принятое в русскоязычной литературе написание фамилии; правильное произношение  Рютерсверд), швед. Oscar Reutersvärd (р. 29 ноября 1915, Стокгольм, Швеция 2 февраля 2002, Лунд)  «отец невозможной фигуры»,… …   Википедия

• Рутерсвард Оскар — Треугольник Пенроуза Оскар Рутерсвард (принятое в русскоязычной литературе написание фамилии; правильное произношение  Рютерсверд), швед. Oscar Reutersvärd (р. 29 ноября 1915, Стокгольм, Швеция 2 февраля 2002, Лунд)  «отец невозможной фигуры»,… …   Википедия

• Невозможная фигура

  — Две известные невозможные фигуры  невозможный треугольник и невозможный х зубец. Невозможная фигура  один из видов оптических иллюзий, фигура, кажущаяся на первый взг …   Википедия

• Рутерсвард, Оскар — Оскар Рутерсвард швед. Oscar Reutersvärd Дата рождения: 29 ноября 1915(1915 11 29) Место рождения …   Википедия

Что такое невозможный треугольник — MicroArticles

Невозможный треугольник — один из удивительных математических парадоксов. При первом взгляде на него ни на секунду не можешь усомниться в его реальном существовании. Однако это только иллюзия, обман. А саму возможность такой иллюзии объяснит нам математика!

Открытие Пенроузов

В 1958 году Британский психологический журнал опубликовал статью Л. Пенроуза и Р. Пенроуза, в которой они ввели в рассмотрение новый тип оптической иллюзии, названной ими «невозможный треугольник».

Зрительно невозможный треугольник воспринимается как реально существующая в трехмерном пространстве конструкция, составленная из прямоугольных брусков. Но это всего лишь оптическая иллюзия. Построить реальную модель невозможного треугольника нельзя.

Статья Пенроузов содержала несколько вариантов изображения невозможного треугольника. — его «классическое» представление.

Из каких элементов строится невозможный треугольник?

Точнее, из каких элементов он кажется нам построенным? В основе конструкции лежит прямоугольный уголок, который получается соединением под прямым углом двух одинаковых прямоугольных брусков. Таких уголков требуется три штуки, а брусков, стало быть, шесть штук. Эти уголки надо определенным образом зрительно «соединить» один с другим так, чтобы они образовали замкнутую цепь. То, что получится, и есть невозможный треугольник.

Первый уголок поместим в горизонтальной плоскости. К нему присоединим второй уголок, направив одно из его ребер вверх. Наконец, к этому второму уголку пристроим третий уголок так, чтобы его ребро было параллельно исходной горизонтальной плоскости . При этом два ребра первого и третьего уголков будут параллельны и направлены в разные стороны.

Если считать брусок отрезком единичной длины, то концы брусков первого уголка имеют координаты , и , второго уголка — , и , третьего — , и . Мы получили реально существующую в трехмерном пространстве «закрученную» конструкцию .

А теперь попробуем мысленно посмотреть на нее из разных точек пространства . Представьте, как она выглядит из одной точки, из другой, из третьей. При изменении точки наблюдения будет казаться, что два «концевых» ребра наших уголков перемещаются относительно друг друга. Не трудно подобрать такое положение, при котором они соединятся .

Но если расстояние между ребрами намного меньше расстояния от уголков до точки, из которой мы рассматриваем нашу конструкцию, то оба ребра будут иметь для нас одинаковую толщину, и возникнет представление о том, что эти два ребра — на самом деле продолжение один другого. Такая ситуация изображена 4.

Кстати, если мы одновременно посмотрим на отражение конструкции в зеркале, то там замкнутой цепи не увидим.

А из выбранной точки наблюдения мы собственными глазами видим свершившееся чудо: имеется замкнутая цепь из трех уголков. Только не меняйте точку наблюдения, чтобы эта иллюзия не разрушилась. Теперь можно нарисовать видимый вам объект или поместить в найденную точку объектив фотоаппарата и получить фотографию невозможного объекта.

Первыми этим явлением заинтересовались Пенроузы. Они использовали возможности, которые возникают при отображении трехмерного пространства и трехмерных объектов на двумерную плоскость и обратили внимание на некоторую неопределенность проектирования — незамкнутая конструкция из трех уголков может восприниматься как замкнутая цепь.

Доказательство невозможности треугольника Пенроузов

Анализируя особенности двумерного изображения трехмерных объектов на плоскости, мы поняли, как особенности этого отображения приводят к невозможному треугольнику. Возможно, кого-то заинтересует и чисто математическое доказательство.

Доказать, что невозможный треугольник не существует, крайне легко, ведь каждый его угол прямой, а их сумма равна 270 градусов вместо «положенных» 180 градусов.

Более того, даже если мы будем рассматривать невозможный треугольник, склеенный из уголков, меньших 90 градусов, то в этом случае можно доказать, что невозможный треугольник не существует.

Мы видим три плоские грани . Они попарно пересекаются вдоль прямых. Плоскости, содержащие эти грани, попарно ортогональны, поэтому они пересекаются в одной точке.

Кроме того, через эту точку должны проходить линии взаимного пересечения плоскостей. Следовательно, прямые линии 1, 2, 3 должны пересекаться в одной точке.

Но это не так. Следовательно, представленная конструкция невозможна.

«Невозможное» искусство

Судьба той или иной идеи — научной, технической, политической — зависит от очень многих обстоятельств. И далеко не в последнюю очередь от того, в какой именно форме эта идея будет представлена, в каком образе она явится широкой публике. Будет ли воплощение сухим и сложным для восприятия, или, наоборот — явление идеи будет ярким, захватывающим наше внимание даже вопреки нашей воле.

У невозможного треугольника судьба счастливая. В 1961 г. голландский художник Мориц Эшер завершил литографию, названную им «Водопад» . Художник прошел немалый, но быстрый путь от самой идеи невозможного треугольника до ее потрясающего художественного воплощения. Напомним, статья Пенроузов появилась в 1958 году.

В основе «Водопада» — два невозможных треугольника, показанных. Один треугольник — большой, внутри него расположен другой треугольник. Может показаться, что изображены три одинаковых невозможных треугольника. Но не в этом суть, представленная конструкция достаточно сложная.

При беглом взгляде ее абсурдность не всякому и не сразу будет видна, так как каждое соединение, представленное , — возможно. как говорят, локально, то есть на небольшом участке чертежа, такая конструкция осуществима… Но в целом она невозможна! Ее отдельные куски не стыкуются, не согласуются друг с другом.

А чтобы понять это, мы должны затратить определенные интеллектуальные и зрительные усилия.

Давайте совершим путешествие по граням конструкции. Этот путь замечателен тем, что вдоль него, как нам кажется , уровень относительно горизонтальной плоскости остается неизменным. Двигаясь вдоль этого пути, мы ни вверх не поднимаемся, ни вниз не опускаемся.

И все-то было бы хорошо, привычно, если бы в конце пути — а именно в точке — мы не обнаружили бы, что относительно исходной, начальной точки мы каким-то таинственным немыслимым образом поднялись вверх по вертикали!

Чтобы прийти к этому парадоксальному результату, мы должны выбрать именно этот путь, да еще следить за уровнем относительно горизонтальной плоскости… Непростая задача. В ее решении Эшеру на помощь пришла…вода. Вспомним песню о движении из чудесного вокального цикла Франца Шуберта «Прекрасная Мельничиха»:

И сначала в воображении, а затем под рукой замечательного мастера голые и сухие конструкции превращаются в акведуки , по которым бегут чистые и быстрые потоки воды. Их движение захватывает наш взгляд, и вот уже помимо нашей воли мы устремляемся по течению, следуя всем поворотам и изгибам пути, вместе с потоком срываемся вниз, падаем на лопасти водяной мельницы, затем снова устремляемся вниз по течению…

Обходим этот путь раз, другой, третий… и только тут осознаем: двигаясь в н и з, мы каким-то фантастическим образом подымаемся в в е р х! Первоначальное удивление перерастает в некий интеллектуальный дискомфорт. Кажется, что мы стали жертвой какого-то розыгрыша, объектом какой-то шутки, которую пока еще не поняли.

И снова мы повторяем этот путь по странному водоводу, теперь уже не спеша, с осторожностью, словно опасаясь подвоха со стороны парадоксальной картинки, критически воспринимая все то, что происходит на этом таинственном пути.

Мы пытаемся разгадать ту тайну, которая поразила нас, и не можем вырваться из ее плена до тех пор, пока не найдем скрытую пружину, лежащую в ее основе и приводящую немыслимую круговерть в безостановочное движение.

Художник специально подчеркивают, навязывает нам восприятие его картины как изображения реальных трехмерных объектов. Объемность подчеркивается изображением вполне реальных многогранников на башнях, кирпичной кладкой с аккуратнейшим представлением каждого кирпича в стенах акведука, поднимающимися вверх террасами с садами на заднем плане. Все призвано убедить зрителя в реальности происходящего. И благодаря искусству и великолепной технике эта цель достигнута.

Когда же мы вырываемся из плена, в который попадает наше сознание, начинаем сравнивать, сопоставлять, анализировать, то находим что основа, источник этой картины скрыты в особенностях проектирования.

И мы получили еще одно — «физическое» доказательство невозможности «невозможного треугольника»: если бы такой треугольник существовал, то существовал бы и «Водопад» Эшера, который есть по сути дела вечный двигатель. Но вечный двигатель невозможен, следовательно, невозможен и «невозможный треугольник». И, наверное, это «доказательство» — самое убедительное.

Что сделало Морица Эшера феноменом, уникумом, который не имел в искусстве явных предшественников и которому невозможно подражать? Это комбинация плоскостей и объемов, пристальное внимание к причудливым формам микромира — живого и неживого, к необычным точкам зрения на обычные вещи. Основной эффект его композиций — эффект появления невозможных отношений между знакомыми предметами. Эти ситуации с первого взгляда могут и напугать, и вызвать улыбку. Можно радостно смотреть на забаву, которую предлагают художник, а можно серьезно погрузиться в глубины диалектики.

Мориц Эшер показал, что мир может быть совсем не таким, каким мы его видим и привыкли воспринимать — надо только посмотреть на него под другим, новым углом зрения!

Мориц Эшер

Морицу Эшеру более повезло как ученому, чем как художнику. В его гравюрах и литографиях видели ключи к доказательству теорем или оригинальные контрпримеры, бросающие вызов здравому смыслу. На худой конец их воспринимали как прекрасные иллюстрации к научным трактатам по кристаллографии, теории групп, когнитивной психологии или компьютерной графике. Мориц Эшер работал в области соотношений пространства, времени и их тождественности, использовал базовые образцы мозаик, применяя к ним трансформации. Это великий мастер оптических обманов. Гравюры Эшера изображают не мир формул, а красоту мира. Их интеллектуальный склад коренным образом противоположен алогичным творениям сюрреалистов.

Голландский художник Мориц Корнелиус Эшер родился 17 июня 1898 года в провинции Голландии. В доме, котором родился Эшер, сейчас находится музей.

С 1907 года Мориц учится плотницкому делу и игре на пианино, обучается в средней школе. Оценки по всем предметам у Морица были плохими за исключением рисования. Учитель рисования заметил талант у мальчика и научил его делать гравюры по дереву.

В 1916 году Эшер выполняет свою первую графическую работу, гравюру на фиолетовом линолеуме — портрет своего отца Г. А. Эшера. Он посещает мастерскую художника Герта Стигемана, имевшего печатный станок. На этом станке были отпечатаны первые гравюры Эшера.

В 1918-1919 годах Эшер посещает Технический колледж в голландском городке Дельфт. Он получает отсрочку от службы в армии для продолжения учебы, но из-за плохого здоровья Мориц не справился с учебным планом, и был отчислен. В результате, он так и не получил высшего образования. Он учится в Школе архитектуры и орнамента в городе Гаарлеме, Там он берет уроки рисования у Самюэля Джесерена де Месквита, оказавшего формирующее влияние на жизнь и творчество Эшера.

В 1921 году семья Эшера посетила Ривьеру и Италию. Очарованный растительностью и цветами средиземноморского климата, Мориц сделал детальные рисунки кактусов и оливковых деревьев. Он зарисовал много эскизов горных пейзажей, которые позже легли в основу его работ. Позже он будет постоянно возвращаться в Италию, которая будет служить для него источником вдохновения.

Эшер начинает экспериментировать в новом для себя направлении, уже тогда в его работах встречаются зеркальные отображения, кристаллические фигуры и сферы.

Конец двадцатых годов оказалась очень плодотворным периодом для Морица. Его работы демонстрировались на многих выставках Голландии, а к 1929 году его популярность достигла такого уровня, что за один год прошли пять персональных выставок в Голландии и Швейцарии. Именно в этот период картины Эшера впервые были названы механическими и «логическими».

Эшер много путешествует. Живет в Италии и Швейцарии, Бельгии. Изучает мавританские мозаики, делает литографии, гравюры. На основе эскизов путешествий он создает свою первую картину невозможной реальности Still Life with Street.

В конце тридцатых годов Эшер продолжает эксперименты с мозаиками и трансформациями. Он создает мозаику в виде двух птиц, летящих навстречу друг другу, которая легла в основу картины «День и ночь».

В мае 1940 года нацисты оккупируют Голландию и Бельгию, а 17 мая в зону оккупации попадает и Брюссель, где на тот момент проживал Эшер с семьей. Они находят дом в Варне и переезжают туда в феврале 1941 года. До конца своих дней Эшер будет жить в этом городе.

В 1946 году Эшер начинает интересоваться технологией глубокой печати. И хотя эта технология была намного сложнее той, которой пользовался Эшер до этого и требовала больше времени для создания картины, но результаты были впечатляющими — тонкие линии и точная передача теней. Одна из самых известный работ в технике глубокой печати «Капля росы» была закончена в 1948 году.

В 1950 году Мориц Эшер обретает популярность как лектор. Тогда же в 1950 году проходит его первая персональная выставка в Соединенных Штатах и начинают покупаться его работы. 27 апреля 1955 года Морица Эшера посвящают в рыцари и он становится дворянином.

В середине 50-х годов Эшер объединяет мозаику с фигурами, уходящими в бесконечность.

В начале 60-х годов вышла в свет первая книга с работами Эшера «Grafiek en Tekeningen», в которой 76 работ прокомментировал сам автор. Книга помогла обрести понимание среди математиков и кристаллографов, включая некоторых из России и Канады.

В августе 1960 Эшер прочитал лекцию по кристаллографии в Кембридже. Математические и кристаллографические аспекты творчества Эшера становятся очень популярными.

В 1970 году после новой серии операций Эшер переехал в новый дом в Ларене , в котором была студия, но плохое здоровье не давало возможности много работать.

В 1971 году Мориц Эшер скончался в возрасте 73 лет. Эшер прожил достаточно долго, чтобы увидеть книгу «Мир М. К. Эшера», переведенную на английский язык и остался ею очень доволен.

Различные невозможные картины встречаются на сайтах математиков и программистов. Самой полной версией из просмотренных нами, на наш взгляд, является сайт Влада Алексеева

На этом сайте представлены не только широко известные картины, в том числе и М. Эшера, но, и анимированные изображения, забавные рисунки невозможных животных, монет, марок и т.п. Этот сайт живет, он периодически обновляется и пополняется удивительными рисунками.

Треугольник Пенроуза – Онлайн-курсы школы «Юниверс»

Невозможные фигуры всегда будоражат сознание творческих людей. Еще бы! При помощи карандаша и листа бумаги взять и отменить целую геометрию Эвклида, разве это не заманчиво? Сегодня мы вооружимся более сложным инструментом, чем карандаш, и построим в Adobe Illustrator знаменитый треугольник Пенроуза, одну из самых известных «невозможных фигур».

Она была открыта в 1934 году шведским художником Оскаром Реутерсвардом, который изобразил его в виде набора кубиков (так, как мы его сегодня и нарисуем). В 1980 году этот вариант невозможного треугольника был напечатан на шведских почтовых марках.

Широкую известность эта фигура обрела после опубликования статьи о невозможных фигурах в Британском журнале психологии английским математиком Роджером Пенроузом в 1958 году. В этой статье невозможный треугольник был изображен в наиболее общей форме — в виде трёх балок, соединённых друг с другом под прямыми углами. Под влиянием этой статьи в 1961 голландский художник Мауриц Эшер создал одну из своих знаменитых литографий «Водопад».

 

 

Шаг 1.

Cоздайте три квадрата, используя инструмент Rectangle tool.

Шаг 2.

Для удобства рисования зайдите в меню View > включите функцию Smart Guides. Направляющие подскажут, где линии пересечения, где перпендикуляр, и даже обозначат середину объекта.

Шаг 3.

Выделите все три объекта, перейдите в меню Object > Transform > Transform each. В появившемся окне в секции Scale задайте значение  Vertical Scale = 86,6% > OK.

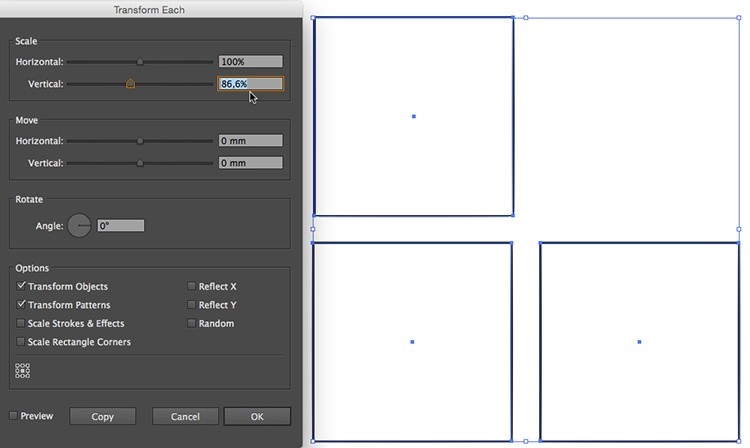
Александр Сераков: Этот шаг может показаться чистым шаманизмом, но без него не получится превратить наши квадратики в плоскости изометрической проекции.

Шаг 4.

Задайте всем граням кубика нужный угол поворота.  Перейдите в меню Window > Transform > в панели Transform сначала вводите значение для Shear, и только потом для Rotate.

Верхняя грань: Shear +30º, Rotate -30º;

Левая грань: Shear -30º, Rotate -30º;

Правая грань: Shear +30º, Rotate +30º.

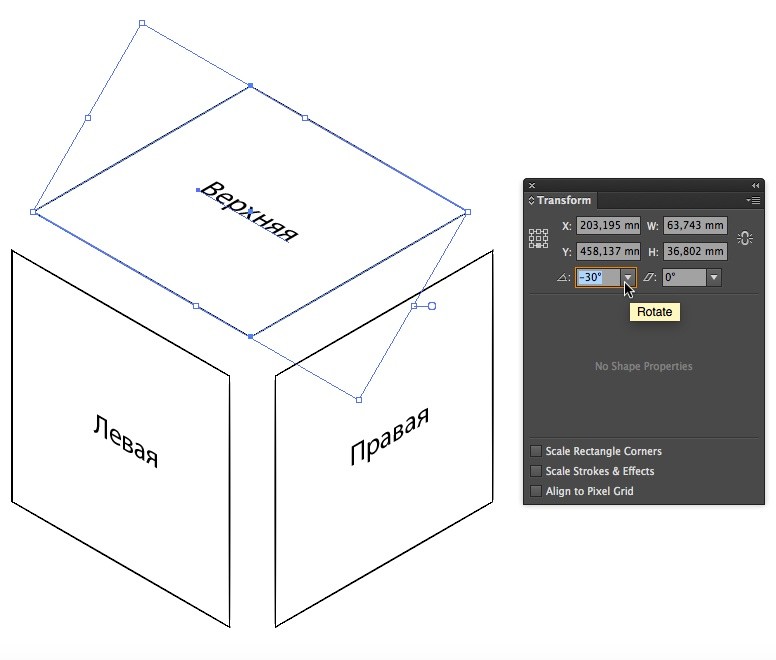
А.С.: Порядок действий здесь имеет важное значение — сначала скос (shear), потом поворот (rotate), не наоборот! Стороны же можно выбирать в любом порядке, лишь бы не путать, что куда поворачивать.

Шаг 5.

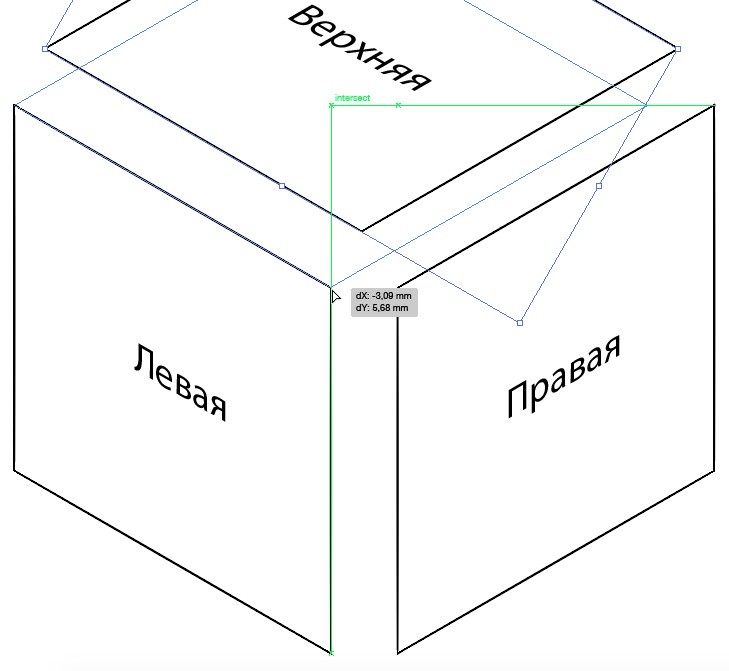
Соедините объекты так, чтобы получился куб. Для этого возьмитесь за уголок одной из сторон и аккуратно потяните его к другой стороне, таким образом совместив их. Линии Smart Guides помогут вам ровно состыковать все три части между собой.

Шаг 6.

Раскрасьте кубик, используя палитру Swatches (ее можно вызвать через меню Window > Swatches). Задайте цвет заливки и обводки на свой вкус.

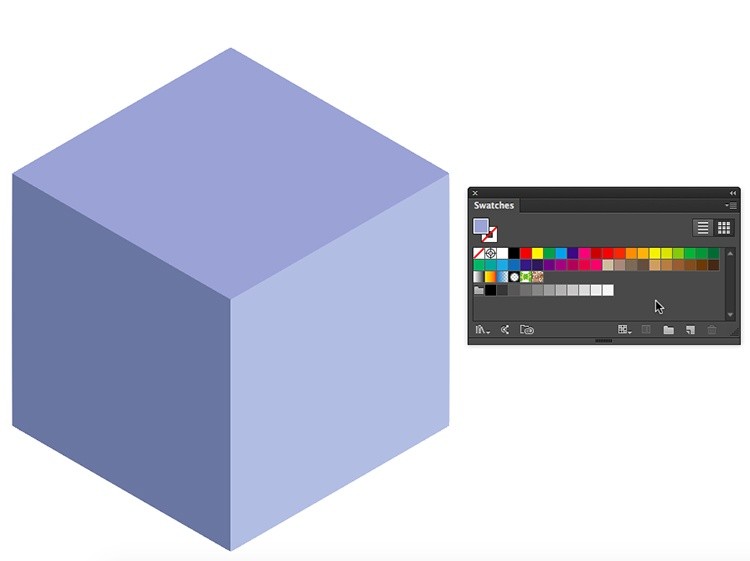
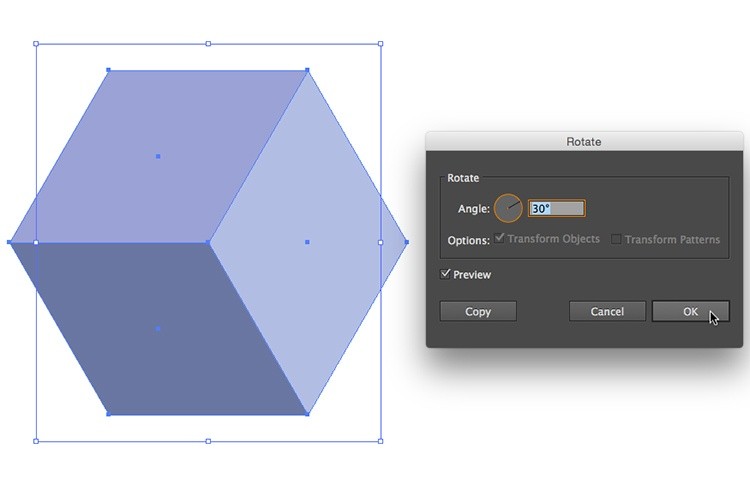
Шаг 7.

Поверните кубик на 30°. Для этого выделите кубик еще раз, перейдите в меню Object > Transform > Rotate > выставите значение Angle 30º > OK

Шаг 8.

Чтобы сделать целый треугольник Пенроуза, нам нужно много таких же кубиков. Выделите получившийся кубик инструментом Selection Tool > зажмите клавишу Alt и потяните. Линии Smart Guides будут подсказывать вам направление.  Если ориентироваться на линии Smart Guides для вас не очень удобно, то, после того как вы зажали Alt и начали тянуть кубик в сторону, также зажмите клавишу Shift. Таким образом копия будет перемещаться строго по горизонтали, без смещений. Не снимайте выделение. 

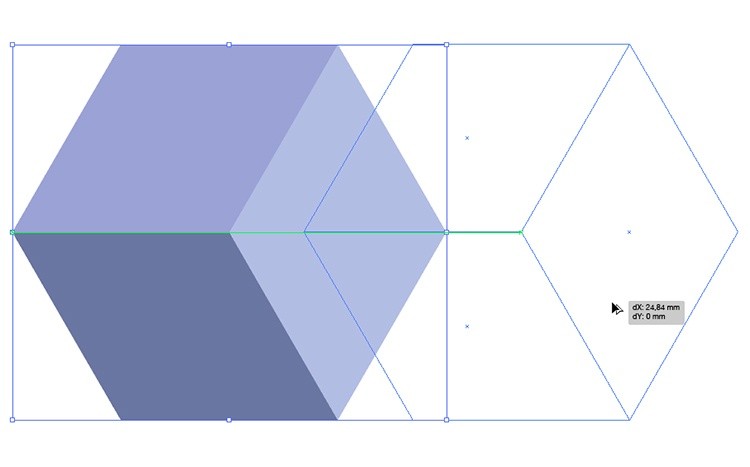
Теперь сделать оставшиеся копии будет гораздо проще. Нажимайте сочетание клавиш CMD + D до тех пор, пока не получите 6 копий кубиков.

Шаг 9.

Когда ряд из 6 кубиков будет готов, не убирайте выделение с последнего, а нажмите клавишу Enter. В открывшемся окне Move измените значение Angle на 240º > нажмите Copy. Создадим еще одну сторону треугольника. Как и в предыдущем шаге, нажимайте клавиши CMD + D до тех пор, пока не создадите нужное количество копий.

А.С.: Это самая необычная горячая клавиша Adobe Illustrator. Обычно мы используем Enter для подтверждения действия, это аналог кнопки OK. Но создатели Illustrator решили, что двигать объекты вам приходится чаще, негоже пропадать такой красивой кнопке, и назначили ей вызов команды Move.

Шаг 10.

Как только дойдете до конца, опять выделите последний кубик и нажмите Enter. В уже знакомом вам окне Move задайте значение Angle 120º и нажмите Copy > с помощью клавиш CMD + D сделайте на этой стороне только 5 кубиков.

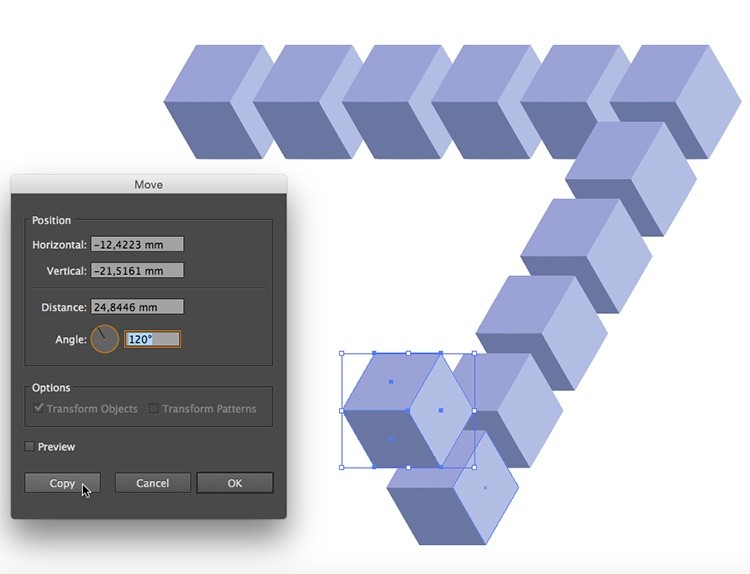
Шаг 11.

Инструментом Selection Tool выделите верхнюю грань кубика (чтобы было понятнее, мы перекрасили ее в желтый цвет) > зайдите в меню Object > Arrange > Send to back.

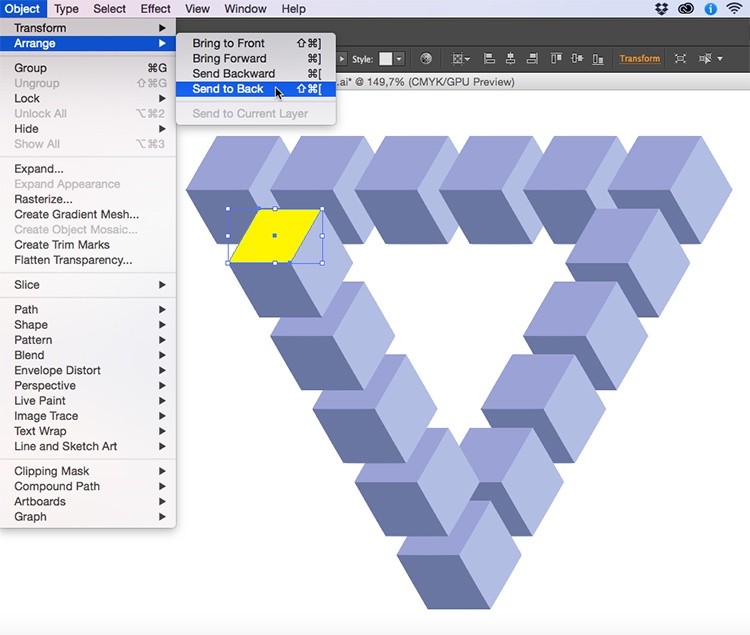
После этого выберите желтую грань верхнего кубика > зайдите в меню Object > Arrange > Bring to Front.

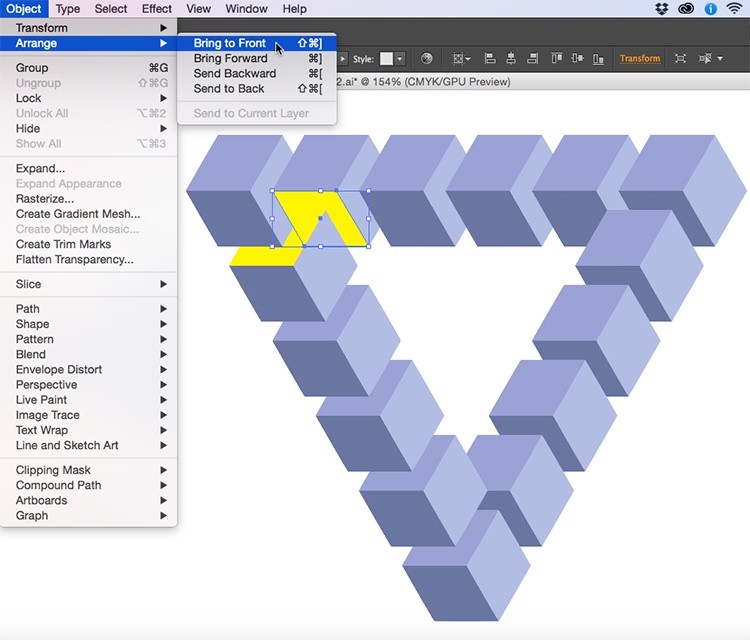
А.С.: По-моему, это самый забавный элемент урока. Существует множество способов, как обойти «парадокс ромашки» — в Illustrator все объекты лежат в общей стопке, и никак нельзя подсунуть верхний объект под нижний, не меняя их порядок. Здесь можно выкрутиться, меняя порядок отдельных элементов кубиков. Будь это не кубики, а целые объекты, пришлось бы прибегать к сложной процедуре вырезания фрагментов. Мы обязательно вернемся однажды к этой теме — «парадокс ромашки» не должен  вызывать у вас трудности!

Наш треугольник Пенроуза готов!

Треугольник Пенроуза — это… Что такое Треугольник Пенроуза?

Треугольник (значения) — В Викисловаре есть статья «треугольник» Треугольник в широком смысле  объект треугольной формы, либо тройка объектов, попарно связ …   Википедия

Невозможный треугольник — Треугольник Пенроуза Скульптура невозможного треугольника, Перт, Австралия Треугольник Пенроуза  одна из основных невозможных фигур, известная также под названиями невозможный треугольник и трибар. Был открыт в 1938 году шведским художником …   Википедия

Оскар Реутерсвард — Треугольник Пенроуза Оскар Рутерсвард (принятое в русскоязычной литературе написание фамилии; правильное произношение  Рютерсверд), швед. Oscar Reutersvärd (р. 29 ноября 1915, Стокгольм, Швеция 2 февраля 2002, Лунд)  «отец невозможной фигуры»,… …   Википедия

Оскар Рутерсвард — Треугольник Пенроуза Оскар Рутерсвард (принятое в русскоязычной литературе написание фамилии; правильное произношение  Рютерсверд), швед. Oscar Reutersvärd (р. 29 ноября 1915, Стокгольм, Швеция 2 февраля 2002, Лунд)  «отец невозможной фигуры»,… …   Википедия

Реутерсвард — Треугольник Пенроуза Оскар Рутерсвард (принятое в русскоязычной литературе написание фамилии; правильное произношение  Рютерсверд), швед. Oscar Reutersvärd (р. 29 ноября 1915, Стокгольм, Швеция 2 февраля 2002, Лунд)  «отец невозможной фигуры»,… …   Википедия

Реутерсвард О. — Треугольник Пенроуза Оскар Рутерсвард (принятое в русскоязычной литературе написание фамилии; правильное произношение  Рютерсверд), швед. Oscar Reutersvärd (р. 29 ноября 1915, Стокгольм, Швеция 2 февраля 2002, Лунд)  «отец невозможной фигуры»,… …   Википедия

Реутерсвард, Оскар — Треугольник Пенроуза Оскар Рутерсвард (принятое в русскоязычной литературе написание фамилии; правильное произношение  Рютерсверд), швед. Oscar Reutersvärd (р. 29 ноября 1915, Стокгольм, Швеция 2 февраля 2002, Лунд)  «отец невозможной фигуры»,… …   Википедия

Реутерсвард Оскар — Треугольник Пенроуза Оскар Рутерсвард (принятое в русскоязычной литературе написание фамилии; правильное произношение  Рютерсверд), швед. Oscar Reutersvärd (р. 29 ноября 1915, Стокгольм, Швеция 2 февраля 2002, Лунд)  «отец невозможной фигуры»,… …   Википедия

Рутерсвард Оскар — Треугольник Пенроуза Оскар Рутерсвард (принятое в русскоязычной литературе написание фамилии; правильное произношение  Рютерсверд), швед. Oscar Reutersvärd (р. 29 ноября 1915, Стокгольм, Швеция 2 февраля 2002, Лунд)  «отец невозможной фигуры»,… …   Википедия

Эшер, Мауриц Корнелис — В Википедии есть статьи о других людях с такой фамилией, см. Эшер. Мауриц Корнелис Эшер Автопортрет, 1929 год Имя при рождении: Maurits Cornelis Escher Дата рождения …   Википедия

Невозможный треугольник — Индекс иллюзий

«Невозможный треугольник» (также известный как «Треугольник Пенроуза» или «Невозможный треугольник») был впервые создан Оскаром Реутерсвардом (1915–2002), шведским художником-графиком, известным как «отец невозможной фигуры». Это анекдотично, но широко сообщается, что он создал его в 1934 году, когда ему было 18 лет, когда он рисовал на уроке латыни. Иллюзия была независимо открыта позже и популяризирована Лайонелом Шарплсом Пенроузом (1898-1972), британским психиатром, генетиком и математиком, и его сыном сэром Роджером Пенроузом (1931 -), британским математиком, физиком и философом науки.Пенроуз и Пенроуз опубликовали иллюзию в Британском журнале психологии в 1958 году.

Треугольник Пенроуза — невозможная фигура (или невозможный объект, или неразрешимая фигура): он изображает объект, который не может существовать. Невозможный треугольник не может существовать, потому что для его существования должны быть нарушены правила евклидовой геометрии. Например, нижняя полоса трибара представлена ​​как пространственно расположенная как спереди, так и сзади самой верхней точки трибара.

Четырехстороннее невозможное изображение

Невозможный треугольник имеет три стороны. Существуют версии невозможных фигур с четырьмя и более сторонами, а также в различных конфигурациях и контекстах. (См. Рисунки ниже и изучите другие невозможные фигуры в Индексе иллюзий.) Такие художники, как Оскар Реутерсвард (см. Ниже) и М. К. Эшер (например, см. Бельведер), часто использовали в своих работах невозможные фигуры разных типов.

Математики изучали математические и вычислительные свойства невозможных фигур, чтобы попытаться разработать формулы и алгоритмы моделирования невозможных объектов для использования в таких вещах, как компьютерное зрение.Когнитивных ученых интересовали процессы, связанные с продолжением видеть невозможные фигуры возможными, даже когда мы знаем, что они невозможны. Почему, например, мы не видим невозможный треугольник как несколько строк на странице, когда понимаем, что он не может существовать в трехмерном пространстве? При ответе на этот вопрос центральное значение имеют дебаты о модульности и когнитивном проникновении. Для объяснения: согласно гипотезе о модульности разума, ментальный модуль является своего рода полунезависимым отделом разума, который имеет дело с определенными типами входных данных и дает определенные типы выходных данных, и чья внутренняя работа недоступна для осознанная осведомленность о человеке — все, к чему можно получить доступ, это соответствующие результаты.Итак, в случае невозможных фигур стандартный способ объяснения того, почему переживание невозможной фигуры сохраняется, даже если кто-то знает, что он переживает невозможное, заключается в том, что модуль или модули, составляющие визуальную систему, « когнитивно непроницаемы » для в некоторой степени — то есть на их внутреннюю работу и результаты не может повлиять сознательная осведомленность. Философов также интересовало, что невозможные фигуры могут сказать нам о природе содержания опыта.Например, невозможные фигуры, кажется, предоставляют примеры опыта с противоречивым содержанием, что некоторые философы сочли против утверждения о том, что состояния восприятия подобны убеждениям (Macpherson 2010).

Оскар Реутерсвард создал множество других красивых и убедительных версий невозможных фигур:

Ричард Грегори (1968) создал деревянный объект, который, когда и только когда рассматривается из одной точки в пространстве, кажется настоящим трехмерным невозможным треугольником, но на самом деле это всего лишь три стойки из соединенной древесины, как можно увидеть, когда один рассматривает это с другой стороны:

Скульптура «Невозможный треугольник» была спроектирована художником Брайаном Маккеем и архитектором Ахмадом Абасом и построена на площади Клэйзбрук в Восточном Перте, Австралия.Его высота составляет 13,5 метра, и он был введен в эксплуатацию после того, как был выбран победителем в конкурсе на реконструкцию Восточного Перта:

Momument Valley — игра, выпущенная компанией Ustwo Games в 2014 году и основанная на серии невозможных фигур. Игрок ведет принцессу по поверхности невозможных фигур, манипулируя этими объектами, чтобы добраться до различных мест.

,

Невозможный треугольник — Невозможный мир

Невозможный треугольник был впервые нарисован в 1934 году шведами. художник Оскар Реутерсвард. Он нарисовал свою версию трэнгла как набор кубиков в параллельной проекции. Althow, многие художники использовали невозможное треугольник в своем искусстве, Оскар Реутерсвард открыл фантастический мир невозможных фигур. Он создал тысячи невозможных фигур за свою жизнь, и теперь он известен как «отец» невозможного цифры.В 1980 году правительство Швеции решило разместить невозможный треугольник и две другие его фигуры по почте марки, которые печатались около двух лет ..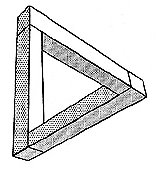

Но форма невозможного треугольника также известна как Трибар Пенроуза . В 1954 году английский математик Роджер Пенроуз после лекция голландского художника М.С. Эшер нарисовал невозможный треугольник это общепринятая точка зрения.В отличие от треугольника Реутерсварда, он нарисовал треугольник в виде трех стержней, соединенных прямыми углами. Он дал перспективный эффект к нему, усиливающий эффект невозможности. Он опубликовал свою версию треугольника в журнале British Psychology Magazine в 1954 г. присоединился к статье его и его отца Лайонела Пенроуза. В 1954 году Эшер не создал свои знаменитые литографии «Водопад», «По возрастанию и Спуск »и« Бельведер ». все же.Отметим, ни Пенроуз, ни Эшер не знали об произведениях искусства. Рейтерсвардом и Пиранези в то время.

.