Невозможные геометрические фигуры: Как рисовать невозможные фигуры

Как рисовать невозможные фигуры

Само это название сбивает с толку: «невозможная форма». Как может быть невозможна любая форма? Если кто-то рисует заданную фигуру, то она существует. И действительно, они могут быть нарисованы, просто не созданы в трех измерениях.

Невозможные фигуры — это тип оптической иллюзии. Когда мы смотрим на рисунок в двумерном изображении, наш мозг автоматически интерпретирует изображенный элемент, как трехмерный объект, поскольку он пытается понять типы и символы. Но в данном случае они рисуются с пространственными несоответствиями, создавая глубину, которой нет — или не может быть в реальной жизни. Подсознание борется обрабатывать рисунки, которые «неправильные», пытаясь превратить их во что-то реальное и понятное для восприятия. Но не может.

Вы удивлены? Давайте посмотрим на некоторые невозможные формы, и как Вы сможете их нарисовать. Это поможет лучше понять, что они представляют, и как работают.

Самые известные невозможные формы

Представим четыре изо всех самых известных невозможных фигур:

• треугольник Пенроуза (или ещё называют трибар),
• лестница Пенроуза,
• оптический ящик
• невозможный трезубец.

Треугольник Пенроуза

Оптический ящик

Лестница Пенроуза

Все они предоставляют возможности, как для ценного исследования человеческих перцептивных процессов, так и для того, чтобы принести радость и очарование. Такие работы раскрывают бесконечное увлечение человечества творчеством и необычностью. Эти примеры также могут помочь нам понять, что наше собственное восприятие может быть ограниченным или отличаться от восприятия другим человеком того же самого.

Как нарисовать невозможные фигуры?

Представьте следующее. Вам захотелось попробовать свои силы в рисовании, чтобы воссоздать невозможную форму. Это не удивительно. Помните, как весело было в детстве, когда кто-то впервые показал вам, как рисовать куб? Вы нарисуете один квадрат, затем другой, который был наполовину сверху первого, а затем соедините их диагональными линиями. И вот Вам куб!

В то время, когда существует много сложных невозможных форм, которые бы трудно дались большинству людей, Вы можете использовать один простой метод, чтобы создать одну из многих распространенных форм: квадраты, треугольники, звезды и пятиугольники. Давайте нарисуем треугольник.

• Нарисуйте треугольник.
• Продлите линию от каждого угла.
• Нарисуйте другую линию от каждого из этих расширений, которые немного простираются по углам.
• Мы почти закончили! В конце каждой линии нарисуйте короткий 45-градусный угол, который выравнивается с противоположной стороны.
• Теперь забавная часть: Соедините линии, и вы будете иметь невозможную форму!

Используйте этот базовый набор инструкций для создания невозможных фигур из других форм. Это должно быть довольно легко.

Как невозможные формы вдохновляют искусство

Невозможные объекты завораживают. Вы можете изучать их в течение длительных периодов времени, прослеживая их линии, пытаясь понять, где именно «трюк» заключается в том, что они выглядят реальными, и в то же время нереальными. Неудивительно, что они часто вдохновляют художников на их воссоздание. Наверное, самым известным художником в мире невозможных конструкций является М. К. Эшер.

Мауриц Эшер (Maurits Escher) – родившийся в Нидерландах, выдающийся голландский художник-графист, известен во всем мире, как мастер графических иллюзий.

Он составил около 450 литографии, ксилографии и гравюры на дереве в течение своей жизни, плюс более 2000 рисунков и набросков. Он был очарован невозможными предметами и способствовал популяризации треугольника Пенроуза, который он включил во многие свои работы.

 

Источник:

[Всего: 1   Средний:  5/5]

Научная работа по математике "Невозможные геометрические фигуры"

Инфоурок › Математика ›Научные работы›Научная работа по математике "Невозможные геометрические фигуры"

Описание презентации по отдельным слайдам:

1 слайд Описание слайда:

МОУ СОШ Средняя школа №19 Невозможные геометрические фигуры «Все, что выглядит как волшебство – это просто наука, которую мы еще не поняли». Выполнила Сим Майя, ученица 5 А класса Новоалтайск 2017

2 слайд Описание слайда:

Оглавление 1. Проблемная ситуация, цель, методы исследования 2. Задачи исследования, актуальность 3. Определение невозможных геометрических фигур 4. История возникновения 5. Самые известные виды невозможных фигур 6. Восприятие невозможных фигур – результаты опроса 7. Возможное применение 8. Заключение 9. Список использованной литературы

3 слайд Описание слайда:

1. Проблемная ситуация, цель, методы исследования Недавно я познакомилась с таким явлением как невозможные геометрические фигуры. То, что сначала я приняла за красивые геометрические рисунки, при углубленном изучении оказалось геометрически противоречивыми изображениями объектов, не существующих в реальном трёхмерном пространстве. Мне стало интересно, какие геометрические фигуры можно отнести к невозможным? Кто их придумал, насколько подобные фигуры известны широкой аудитории? Цель исследования– изучение невозможных геометрических фигур и их восприятие разными возрастными группами. Предмет исследования – невозможные геометрические фигуры. Объект исследования – восприятие невозможных геометрических фигур людьми разных возрастных групп. Методы исследования - сбор и обработка информации, работа с источниками профильной литературы, социологический опрос.

4 слайд Описание слайда:

2. Задачи, гипотеза, актуальность исследования Задачи исследования: - изучить литературу, связанную с определением, историей и видами геометрических невозможностей; - произвести отбор иллюстраций невозможных геометрических фигур; - провести опрос среди следующих возрастных категорий: 1) ученики начальных классов (1 – 4 классы) , 2) учащиеся средних классов (5 – 9 классы), 3) ученики старших классов (10 – 11), 4) студенты высших учебных заведений, 5) старше 25 лет. - выявить характерные особенности восприятия. Гипотеза - изучение невозможных геометрических фигур способствует развитию пространственного воображения у людей, относящихся к различным возрастным группам. Существует огромное количество людей, не знающих и не изучающих невозможные геометрические фигуры. Именно поэтому моя работа актуальна. Как показал проведенный мною опрос, подавляющее большинство респондентов никогда не сталкивались с невозможными геометрическими фигурами. К тому же, невозможные фигуры влияют на развитие пространственного мышления и воображения, что всегда актуально и важно.

5 слайд Описание слайда:

3. Определение невозможных фигур Невозможная фигура – это выполненный на бумаге трехмерный объект, который не может существовать в действительности, но который, можно видеть как двухмерное изображение. Есть виды невозможных фигур, которые можно изготовить, но для этого нужно намеренно исказить линии, сделать специальные прорези или вовсе сфотографировать под нужным углом. Я рассматривала невозможные геометрические фигуры без учета этого – в их первоначальном виде. 4.История возникновения невозможных геометрических фигур Картины с искаженной перспективой встречаются уже в начале первого тысячелетия. На миниатюре из книги Генриха II, созданной до 1025 года и хранящейся в баварской государственной библиотеке в Мюнхене, нарисована «Мадонна с младенцем» . На картине изображен свод, состоящий из трех колонн, причем средняя колонна по законам перспективы должна располагаться впереди Мадонны, но находится за ней, что придает картине эффект нереальности.

6 слайд Описание слайда:

Мадонна с младенцем

7 слайд Описание слайда:

Изображения невозможных фигур встречаются у ряда живописцев Средних веков. Основателем же направления невозможного искусства - имп-арта (imp-art, impossible art) считается шведский художник Оскар Рутерсвард. Первая невозможная фигура "Opus 1" нарисована мастером в 1934 году. В 1958 году Роджер Пенроуз опубликовал статью о невозможных фигурах в "Британском журнале психологии". Статья стала первой теоретической работой в этой области и послужила толчком для развития и популяризации картин в стиле имп-арта. Наиболее известным художником имп-арта стал М. К. Эшер .

8 слайд Описание слайда:

5. Самые известные виды невозможных геометрических фигур Фигура «удивительного треугольника» самый известный и первый опубликованный в печати невозможный объект. Она появилась в 1958 году. Её авторы, отец и сын Лайонелл и Роджер Пенроузы, определили этот объект как трехмерную прямоугольную структуру. Она также получила название "трибар. Стороны, сходящиеся вверху рисунка, кажутся перпендикулярными. В тоже время левая и правая грани внизу тоже кажутся перпендикулярными. Также существует и «тройной трибар».

9 слайд Описание слайда:

Треугольник Пенроуза увековечен в городе Перте в Австралии. Он был установлен в 1999 году и теперь все, проходя мимо, могут увидеть невозможную фигуру. Правда, привлекательность и геометрическая целостность фигуры зависят исключительно от угла зрения.

10 слайд Описание слайда:

Следующий известный объект, чья скульптурная реализация в принципе невозможна, «чертова вилка» (другие названия «космическая вилка», «чертов трезубец». Можно заметить, что три зубца постепенно переходят в два на общем основании, приводя к конфликту восприятия. Мы сравниваем число зубцов сверху и снизу и приходим к выводу о невозможности объекта. .

11 слайд Описание слайда:

Литография «Водопад» М.Эшера Вода на картине течет бесконечно, после водяного колеса она проходит дальше и попадает обратно в исходную точку. По сути, это изображение вечного двигателя, но любая попытка в реальности построить данную конструкцию обречена на неудачу.

12 слайд Описание слайда:

Последний пример - бесконечная лестница. Эту фигуру чаще всего называют "Бесконечной лестницей", "Вечной лестницей" или "Лестницей Пенроуза" – по имени ее создателя. Ее также называют непрерывно восходящей и нисходящей тропой. Впервые эта фигура была опубликована в 1958 году.

13 слайд Описание слайда:

Своеобразный аналог бесконечной лестницы - лестница, которая никуда не ведет, но идти в одном направлении можно вечно – был построен в Мюнхене. Название этой лестницы не менее странное - «Перезапись

14 слайд Описание слайда:

6. Восприятие невозможных фигур – результаты опроса. Я опросила десять учеников начальных классов, двенадцать учащихся средних классов, семь учеников старших классов, шесть студентов и десять человек возрастной категории старше 25 лет. Опрашиваемым предлагались для изучения иллюстрации невозможных геометрических фигур. После этого задавались следующие вопросы: 1) Сталкивались ли вы ранее с подобными изображениями? 2) Возможна ли такая фигура в реальности? 3) Видите ли вы какие-либо несоответствия? 4) Считаете ли невозможные геометрические фигуры хорошим способом развивать умственную деятельность, фантазию и пространственное воображение? Из 45 человек оказались знакомы с геометрическими невозможностями лишь двое (старше 25), что лишь подчеркивает актуальность моей работы. Остальные впервые видели подобные изображения. Что касается второго вопроса, то ученики начальных и средних классов ответила сначала «да», но третий вопрос заставил их задуматься, так ли все просто с этими фигурами. Старшие респонденты более тщательно изучали предложенные иллюстрации, и потому находили пространственные нарушения. Однако изображение «Мадонна с младенцем» поставила в затруднение всех. Все без исключения признали, что геометрические невозможности заставили их задуматься о логике и пространстве, «размять мозги», и это отличная «зарядка для ума».

15 слайд Описание слайда:

7. Возможное применение В Швеции стоматологи развешивают иллюстрации в зубных кабинетах, чтобы пациенты отвлекались от неприятного процесса лечения. Русские авторы предлагают то же сделать в местах с большими очередями, чтобы люди отвлекались. Помимо психотерапевтического эффекта невозможные фигуры можно использовать в архитектуре, рекламе для привлечения внимания, оформительском искусстве. Но главное предназначение невозможных фигур – активизировать нашу умственную деятельность, развивать пространственное мышление!

16 слайд Описание слайда:

8. Заключение Очень ценным с точки зрения понимания восприятия невозможных фигур людьми оказался проведенный опрос. Полученные данные показывают, что феномен геометрических невозможностей активизирует умственную деятельность, развивает наше пространственное воображение. К тому же, опрос показал, что данная тема достаточна новая для представителей разных поколений, а потому вызывает интерес и желание разобраться. Закончить свою работу мне бы хотелось определением невозможных фигур О.Рутерсварда: «Это рисунки, которые своей противоречивой структурой поражают взгляд и вызывают у нас желание не останавливаться перед загадочным, а попытаться дать ему приемлемое объяснение. Может быть, уже к концу нашего века будет воздвигнут храм невозможного, освобождающего нас на несколько мгновений от цепей реальности».

17 слайд Описание слайда:

Список использованной литературы 1. Невозможная фигура. Википедия. https://ru.wikipedia.org/wiki/Невозможная_фигура 2. О.Рутерсвард. Невозможные фигуры. http://im-possible.info/russian/articles/reut_imp/ 3. Л. И Р.Пенроузы. Невозможные объекты http://kvant.mccme.ru/1971/05/nevozmozhnye_obekty.htm 4. Д.Раков. Невозможная реальность https://www.nkj.ru/archive/articles/1761/ 5. А.Коненко. Невозможные фигуры. http://www.konenko.net/imp.htm 6.Мир красив! Туристический портал. http://www.mirkrasiv.ru/articles/beskonechnaja-lestnica-perezapis-myunhen-germanija.html 7.А.Загрядская. Невозможные фигуры. https://newtonew.com/science/impossible-objects    

Курс повышения квалификации

Курс повышения квалификации

Курс профессиональной переподготовки

Учитель математики и информатики

Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:

Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое

Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс

Выберите учебник: Все учебники

Выберите тему: Все темы

также Вы можете выбрать тип материала:

Общая информация

Номер материала: ДБ-1536617

Похожие материалы

Вам будут интересны эти курсы:

Оставьте свой комментарий

Невозможные фигуры / Newtonew: новости сетевого образования

На первый взгляд кажется, что невозможные фигуры могут существовать только на плоскости. На самом деле невероятные фигуры могут воплощаться в трёхмерном пространстве, однако для «того самого эффекта» смотреть на них нужно с определённой точки.

Вот, например, скульптура «невозможного треугольника» в Австралии: все его углы равны 90 градусам, чего с треугольниками в обычном мире не случается. Однако с другой точки скульптура выглядит таким образом.

Искажённая перспектива — частое явление в старинной живописи. Где-то это было обусловлено неумением художников выстраивать изображение, где-то — признаком равнодушия к реализму, которому предпочитали символизм. Материальный мир был отчасти реабилитирован в Возрождение. Мастера Ренессанса начали исследовать перспективу и открыли для себя игры с пространством.

Одно из изображений невозможной фигуры относится к XVI веку — на картине Питера Брейгеля Старшего «Сорока на виселице» та самая виселица выглядит подозрительно.

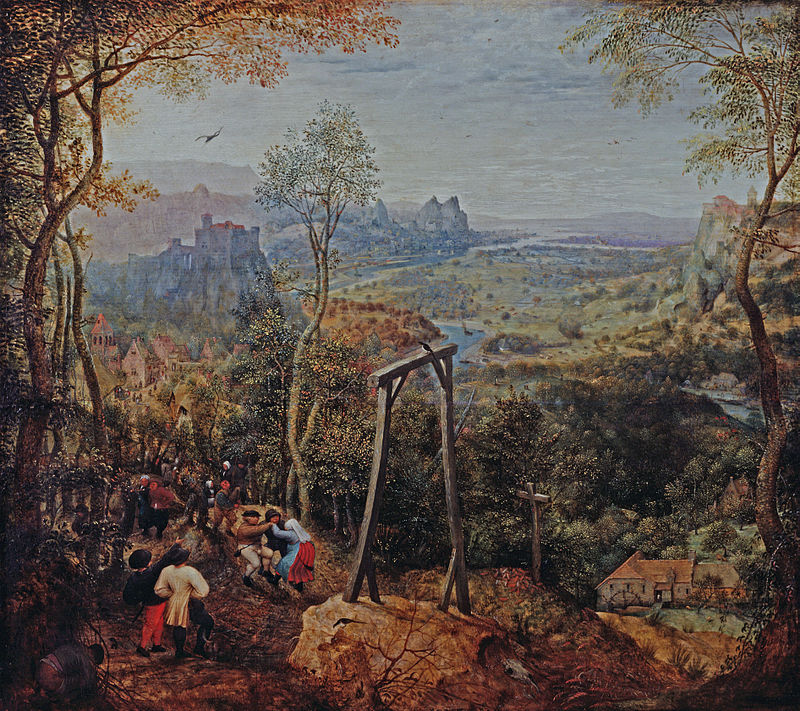
Питер Брейгель Старший, «Сорока на виселице».

Источник: Wikipedia

Большая слава пришла к невозможным фигурам ХХ веке. Шведский художник Оскар Рутесвард в 1934 году нарисовал составленный из кубов треугольник «Opus 1», а несколькими годами позже — «Opus 2B», в котором количество кубов уменьшилось. Сам художник отмечает, что самым ценным в разработке фигур, которую он предпринял ещё в школьные годы, следует считать не создание самих рисунков, а способность понять, что нарисованное парадоксально и противоречит законам евклидовой геометрии.

Моя первая невозможная фигура появилась случайно, когда я в 1934 году в последнем классе гимназии на уроке «чиркал» в учебнике латинской грамматики, рисуя в нем геометрические фигуры.

— Оскар Рутесвард«Невозможные фигуры»

 

В 50-х годах ХХ века вышла статья британского математика Роджера Пенроуза, посвящённая особенностям восприятия пространственных форм, изображённых на плоскости. Статья была опубликована в «Британском журнале психологии», что многое говорит о сущности невозможных фигур. Главное в них — даже не парадоксальная геометрия, а то, как наш разум воспринимает такие явления. Как правило, требуется несколько секунд, чтобы понять, что именно «не так» не так с фигурой.

Благодаря Рождеру Пенроузу на эти фигуры взглянули с точки зрения науки, как на объекты с особыми топологическими характеристиками. Австралийская скульптура, речь о которой шла выше, представляет собой как раз невозможный треугольник Пенроуза, в котором все составляющие реальны, однако в целостность, которая может существовать в трёхмерном мире, картинка не складывается. Треугольник Пенроуза вводит в заблуждение с помощью ложной перспективы.

Загадочные фигуры стали источником вдохновения и для физиков с математиками, и для художников. Вдохновившись статьёй Пенроуза, график Мауриц Эшер создал несколько литографий, которые принесли ему известность художника-иллюзиониста, и впоследствии продолжил экспериментировать с пространственными искажениями на плоскости.

Имп-арт (impossible art) или импоссибилизм — направление в искусстве, в основе которого лежит создание оптических иллюзий и невозможных фигур.

В ХХ веке философия, живопись, литература обратились к уникальным и неповторимым переживаниям субъекта. Главным предметом интереса стали не действия и явления как таковые, а их восприятие, отражение в сознании. Неудивительно, что невозможная геометрия, которая прежде воспринималась как ошибка или курьёз, теперь стала самостоятельным художественным методом.

Вот ещё несколько известных фигур-парадоксов, которые до сих пор продолжают расшатывать разум зрителей.

Модель фигуры была разработана Рождером Пенроузом и его отцом Лайонелом Пенроузом. Изображённая ими лестница делает поворот на 90 градусов и замыкается, так то человек, если бы ему вздумалось по ней взойти, не смог бы подняться выше. На рисунке ниже видно, что собака и человек стоят на одном уровне, что тоже добавляет рисунку невозможности. Если персонажи пойдут по часовой стрелке, то будут постоянно спускаться, а если против часовой — подниматься.

Ранее такую лестницу изображал Оскар Рутесвард, о чём Пенроузы не знали, а Мауриц Эшер популяризировал образ «сумасшедшей лестницы» в искусстве, создав знаменитую работу «Относительность». 

Читайте также: Тайны нашего зрения

Невозможный трезубец, бливет или даже, как его ещё называют, «вилка дьявола», представляет собой фигуру с тремя круглыми зубцами на одном конце и прямоугольными — на другом. Выходит, что объект вполне нормален в правой и левой части, а вот в комплексе получается форменное безумие.

Такой эффект достигается за счет того, что трудно однозначно сказать, где тут передний план, а где задний.

Невозможный куб (он же — «куб Эшера») появился на литографии Маурица Эшера «Бельведер».  Кажется, что самим существованием этот куб нарушает все основные геометрические законы. Разгадка, как и всегда с невозможными фигурами, довольно проста: человеческому глазу свойственно воспринимать двумерные изображения как трёхмерные объекты.

Между тем, в трёх измерениях невозможный куб выглядел бы таким образом и с определённой точки казался бы таким же, как рисунок выше.

---

Невозможные фигуры представляют большой интерес для психологов, когнитивистов и эволюционных биологов, помогая больше узнать о нашем зрении и пространственном мышлении. Сегодня компьютерные технологии, виртуальная реальность и проекции расширяют возможности, так что на противоречивые объекты можно взглянуть с новым интересом.

Кроме классических примеров, которые мы привели, существует множество других вариантов невозможных фигур, а художники и математики придумывают всё новые парадоксальные варианты. Скульпторы и архитекторы используют решения, которые могут показаться невероятными, хотя их вид зависит от направления взгляда зрителя (как Эшер и обещал — относительность!).

Чтобы попробовать себя в создании объёмных невозможностей, профессиональным архитектором быть не обязательно. Существуют оригами невозможных фигур — такое можно повторить дома, скачав заготовку.

Полезные ресурсы

• Невозможный мир — ресурс на русском и английском с известными картинами, сотнями примеров невозможных фигур и программами для самостоятельного создания невероятного.
• M.C. Escher — официальный сайт М.К. Эшера, основанный фондом MC Escher Company (английский и нидерландский языки).
• Мауриц Корнелис Эшер — работы художника, статьи, биография (русский язык).

Оформление статьи: Невозможный куб в 3D Max. Рендеринг: Андрей Устюжанин.

Редакция Newtonew

Алиса Загрядская

Нашли опечатку? Выделите фрагмент и нажмите Ctrl+Enter.

Невозможные фигуры и их моделирование

 

Способность создавать и оперировать пространственными образами характеризует уровень общего интеллектуального развития человека. В психологических исследованиях экспериментально подтверждено, что между склонностью человека к соответствующим профессиям и уровнем развития пространственных представлений имеет место статистически достоверная связь. Широкое применение невозможных фигур в архитектуре, живописи, психологии, геометрии и во многих других областях практической жизни дают возможность больше узнать о различных профессиях и определиться с выбором будущей профессии.

Ключевые слова: трибар, бесконечная лестница, космическая вилка, невозможные ящики, треугольник и лестница Пенроуза, куб Эшера, треугольник Рейтерсвэрда.

 

Цель исследования: изучение свойств невозможных фигур с помощью с помощью 3-D моделей.

Задачи исследования:

1.                Изучить виды и составить классификацию невозможных фигур.
2.                Рассмотреть способы построения невозможных фигур.
3.                Создать невозможные фигуры с помощью компьютерной программы и 3D моделирования.

Понятие невозможных фигур

Объективного понятия «невозможные фигуры» не существует. Из одного источника невозможная фигура — вид оптических иллюзий, фигура, кажущаяся проекцией обычного трёхмерного объекта, при внимательном рассмотрении которой становятся видны противоречивые соединения элементов фигуры. А из другого источника невозможные фигуры — это геометрически противоречивые изображения объектов, не существующих в реальном трёхмерном пространстве. Невозможность возникает из противоречия между подсознательно воспринимаемой геометрией изображённого пространства и формально-математической геометрией.

Анализируя разные определения, приходим к выводу:

невозможная фигура — это плоский рисунок, который создает впечатление трехмерного объекта таким образом, что объект, предложенный нашим пространственным восприятием, не может существовать, так что попытка создать его ведет к (геометрическим) противоречиям, ясно видимыми наблюдателем.

Когда мы смотрим на изображение, которое создает впечатление пространственного объекта, наша система пространственного восприятия пытается найти пространственную форму, определить ориентацию и структуру, начиная с анализа отдельных фрагментов и намеков на глубину. Далее, эти отдельные части комбинируются и координируются в некотором порядке для создания общей гипотезы о пространственной структуре объекта целиком. Обычно, несмотря на то, что плоское изображение может иметь бесконечное множество пространственных интерпретаций, наш механизм интерпретации выбирает только одну — наиболее естественную для нас. Именно эта интерпретация изображения далее проверяется на возможность или невозможность, а не сам рисунок. Невозможная интерпретация получается противоречивой по своей структуре — различные частичные интерпретации не подходят к общему непротиворечивому целому.

Фигуры являются невозможными, если их естественные интерпретации оказываются невозможными. Однако, это не подразумевает, что не существует какой-либо другой интерпретации этой же фигуры, которая может существовать. Таким образом, нахождение метода точного описания пространственных интерпретаций фигур является одним из основных путей для дальнейшей работы с невозможными фигурами и механизмами их интерпретации. Если суметь описать различные интерпретации, то можно будет сравнивать их, соотносить фигуру и ее различные интерпретации (понять механизмы создания интерпретаций), проверять их соответствие или определять типы несоответствия и т. п.

Виды невозможных фигур

Невозможные фигуры разделяются на два больших класса: одни имеют реальные трехмерные модели, а для других такие создать невозможно.

В ходе работы над темой изучены 4 вида невозможных фигур: трибар, бесконечная лестница, невозможные ящики и космическая вилка. Все они уникальны по-своему.

Трибар (треугольник Пенроуза)

 

Это геометрически невозможная фигура, элементы которой не могут быть соединены. Все-таки невозможный треугольник стал возможным. Шведский живописец Оскар Рейтесвэрд в 1934 г. впервые представил миру невозможный треугольник из кубиков. В честь этого события в Швеции издана почтовая марка. Трибар можно сделать из бумаги. Любители оригами нашли способ создать и подержать в руках вещь, которая казалась ранее запредельной фантазией ученого. Однако нас обманывают собственные глаза, когда мы смотрим на проекцию трехмерного объекта из трех перпендикулярных линий. Наблюдателю кажется, что он видит треугольник, хотя на самом деле это не так.

Бесконечная лестница.

 

Конструкция, которая не имеет ни конца, ни края, была придумана биологом Лейонелем Пенроузом и его сыном-математиком Роджером Пенроузом. Впервые модель была опубликована в 1958 г., после чего получила большую популярность, стала классической невозможной фигурой, а ее основная концепция нашла применение в живописи, архитектуре, психологии. Модель ступеней Пенроуза обрела самую большую популярность по сравнению с остальными нереальными фигурами в сфере компьютерных игр, головоломках, оптических иллюзиях. «Вверх по ступеням, ведущим вниз» — так можно охарактеризовать лестницу Пенроуза. Идея этой конструкции заключается в том, что при движении по часовой стрелке ступени ведут все время вверх, а в обратном — вниз. При этом «вечная лестница» состоит всего из четырех пролетов. А значит, всего через четыре лестничных марша путник оказывается там же, откуда начал движение.

Невозможные ящики.

 

Еще один невозможный объект появился в 1966 году в Чикаго в результате оригинальных экспериментов фотографа доктора Чарльза Ф. Кокрана. Многие любители невозможных фигур проводили эксперименты с «Сумасшедшим ящиком». Первоначально автор назвал ее «свободным ящиком» и заявил, что она была «сконструирована для пересылки невозможных объектов в большом количестве». «Сумасшедший ящик» — это вывернутый наизнанку каркас куба. Непосредственным предшественником «Сумасшедшего ящика» была «Невозможная коробка» (автор Эшер), а ее предшественником в свою очередь стал куб Неккера. Он не является невозможным объектом, однако представляет собой фигуру, в которой параметр глубины может восприниматься неоднозначно. Когда мы вглядываемся в куб Неккера, то замечаем, что грань с точкой находится то на переднем, то на заднем плане, она перепрыгивает из одного положения в другое.

Космическая вилка.

 

Среди всех невозможных фигур особое место занимает невозможный трезубец («космическая вилка»). Если закрыть рукой правую часть трезубца, то мы увидим вполне реальную картину — три круглых зуба. Если закрыть нижнюю часть трезубца, то мы тоже увидим реальную картину - два прямоугольных зубца. Но, если рассматривать всю фигуру целиком, то получается, что три круглых зубца постепенно превращаются в два прямоугольных.

Таким образом, можно увидеть, что передний и задний планы данного рисунка конфликтуют. То есть, то что было изначально на переднем плане уходит назад, а задний план (средний зуб) вылезает вперед. Кроме смены переднего и заднего планов в данном рисунке присутствует еще один эффект — плоские грани правой части трезубца становятся круглыми в левой. Эффект невозможности достигается за счет того, что наш мозг анализирует контур фигуры и пытается подсчитать количество зубцов. Мозг сравнивает количество зубцов фигуры в левой и правой части рисунка, из-за чего возникает ощущение невозможности фигуры. Если количество зубцов у фигуры было значительно больше (например, 7 или 8), то этот парадокс был бы менее ярко выражен.

Изготовление моделей невозможных фигур по чертежам

Трехмерная модель — это физически представимый объект, при рассмотрении которого в пространстве становятся видимыми все щели и изгибы, которые уничтожают иллюзию невозможности, и данная модель теряет свое «волшебство». При проецировании данной модели на двухмерную плоскость получается невозможная фигура. Эта невозможная фигура (в отличие от трехмерной модели), создает впечатление невозможного объекта, который может существовать только в воображении человека, но не в пространстве.

Трибар

 

Бумажная модель:

 

Невозможный брусок

Чертеж:

 

Бумажная модель:

 

Построение невозможных фигур в программе Impossible Constructor

Программа Impossible Constructor предназначена для конструирования изображений невозможных фигур из кубиков. Основными недостатками этой программы были сложность выбора нужного кубика (отыскать один нужный кубик из 32-х доступных в программе достаточно тяжело), а также то, что не были предусмотрены все варианты кубиков. Предлагаемая программа предоставляет к выбору полный набор кубиков (64 кубика), а также дает более удобный способ нахождения требуемого кубика при помощи конструктора кубиков.

 

Моделирование невозможных фигур.

Печать 3D моделей невозможных фигур на принтере

В ходе работы модели четырех невозможных фигур распечатаны на 3D принтере.

Треугольник Пенроуза

Процесс создания трибара:

 

Вот что у меня получилось в итоге:

 

Куб Эшера

Процесс создания куба: В конечном итоге получена модель:

 

Лестница Пенроуза (всего через четыре лестничных марша путник оказывается там же, откуда начал движение):

 

Треугольник Рейтерсвэрда (первый невозможный треугольник, состоявший из девяти кубиков):

 

Процесс подготовки к печати дал возможность на практике научиться строить стереометрические фигуры на плоскости, выполнять проекции элементов фигур на заданную плоскость и продумывать алгоритмы построения фигур. Созданные модели помогли наглядно увидеть и проанализировать свойства невозможных фигур, сравнить их с известными стереометрическими фигурами.

«Если не можешь изменить ситуацию, взгляни на нее под другим углом».

Эта цитата непосредственно относится к данной работе. Действительно, невозможные фигуры существуют, если взглянуть на них под определенным углом. Мир невозможных фигур чрезвычайно интересен и многообразен. Они существуют с древних времен по наше время. Их можно встретить практически везде: в искусстве, архитектуре, в массовой культуре, в живописи, в иконописи, в филателистике. Невозможные фигуры представляют большой интерес для психологов, когнитивистов и эволюционных биологов, помогая больше узнать о нашем зрении и пространственном мышлении. Сегодня компьютерные технологии, виртуальная реальность и проекции расширяют возможности, так что на противоречивые объекты можно взглянуть с новым интересом. Существует множество профессий, которые так или иначе связаны с невозможными фигурами. Все они востребованы в современном мире, а потому изучение невозможных фигур является актуальным и нужным.

 

Литература:

 

1.                Реутерсвард О. Невозможные фигуры. — М.: Стройиздат,1990, 206 с.
2.                Левитин Карл Геометрическая рапсодия. — М.: Знание, 1984, -176 с.
3.                Пенроуз Л., Пенроуз Р. Невозможные объекты, Квант, № 5,1971, с.26
4.                Ткачева М. В. Вращающиеся кубики. — М.: Дрофа, 2002. — 168 с.
5.                http://www.im-possible.info/russian/articles/reut_imp/
6.                http://www.impworld.narod.ru/.
7.                Левитин Карл Геометрическая рапсодия. — М.: Знание, 1984, -176 с.
8.                http://www.geocities.jp/ikemath/3Drireki.htm
9.                http://im-possible.info/russian/programs/
10.            https://www.liveinternet.ru/users/irzeis/post181085615
11.            https://newtonew.com/science/impossible-objects
12.            http://www.psy.msu.ru/illusion/impossible.html
13.            http://referatwork.ru/category/iskusstvo/view/73068_nevozmozhnye_figury
14.            http://geometry-and-art.ru/unn.html

Невозможные фигуры - геометрия и искусство

Невозможные фигуры - особый вид объектов в изобразительном искусстве. Как правило их называют так, потому что они не могут существовать в реальном мире.

Более точно, невозможными фигурами называют геометрические объекты, нарисованные на бумаге, которые прозводят впечатление обычной проекции трехмерного объекта, однако, при внимательном рассмотрении становятся видны противоречия в соединениях элементов фигуры.

Невозможные фигуры выделяют в отдельный класс оптических иллюзий.

Невозможные конструкции известны с давних времен. Они встречаются в иконах со средних веков. "Отцом" невозможных фигур считается шведский художник Оскар Реутерсвард, который нарисовал невозможный треугольник, составленный из кубиков в 1934 году.

Известны широкой публике невозможные фигуры стали в 50-х годах прошлого века, после публикации статьи Роджера Пенроуза и Лайонела Пенроуза, в которой были описаны две базовые фигуры - невозможный треугольник (который также называют треугольником Пенроуза) и бесконечная лестница. Эта статья попала в руки известного голландского художника М.К. Эшера, который вдохновленный идеей невозможных фигур создал свои знаменитые литографии "Водопад", "Восхождение и спуск" и "Бельведер". Вслед за ним огромное количество художников по всему миру стали использовать невозможные фигуры в своем творчестве. Наиболее известны среди них Жос де Мей, Сандро дель Пре, Оштван Орос. Работы этих, а также других художников, выделяют в отдельное направление изобразительного искусства - "имп-арт".

Может показаться, что невозможные фигуры действительно не могут существовать в трехмерном пространстве. Есть определенные способы, которые позволяют воспроизвести невозможные фигуры в реальном мире, правда они будут выглядет невозможными только с одной точки обзора.

Наиболее известными невозможными фигурами являются: невозможный треугольник, бесконечная лестница и невозможный трезубец.

Статья  из журнала Наука и жизнь "Невозможная реальность" скачать

Невозможные фигуры: imit_omsu — LiveJournal

Что такое невозможные фигуры?
Введя такой вопрос в поисковую систему, мы получим ответ: «Невозможная фигура — один из видов оптических иллюзий, фигура, кажущаяся на первый взгляд проекцией обычного трёхмерного объекта, при внимательном рассмотрении которой становятся видны противоречивые соединения элементов фигуры. Создаётся иллюзия невозможности существования такой фигуры в трёхмерном пространстве. (Википедия)»
Думаю, для представления и осознания этого понятия нам будет недостаточно такого ответа, поэтому попробуем лучше изучить этот вопрос. И начнем, пожалуй, с истории.

История
В старинной живописи можно встретить такое частое явление как искаженная перспектива. Именно она создавала иллюзию невозможности существования объекта. На картине Питера Брейгеля Старшего «Сорока на виселице» такой фигурой является сама виселица. Но в то время создание подобных «небылиц» — это был не полет фантазии, а скорее все же неумение строить правильно перспективу.


Большой интерес к невозможным фигурам проснулся в ХХ веке.

Шведский художник Оскар Рутесвард, увлеченный созданием чего-то парадоксального и противоречащего законам евклидовой геометрии, создал такие работы: составленный из кубов треугольник «Opus 1», а позже «Opus 2B».

В 50-х годах ХХ века вышла статья британского математика Роджера Пенроуза, посвящённая особенностям восприятия пространственных форм, изображённых на плоскости. Статья заинтересовала большой круг лиц: психологи стали изучать, как наш разум воспринимает такие явления, ученые взглянули на эти невозможные фигуры как на объекты с особыми топологическими характеристиками. Появился Имп-арт (impossible art) или импоссибилизм — направление в искусстве, в основе которого лежит создание оптических иллюзий и невозможных фигур.

Статья Пенроуза вдохновила Маурица Эшера создать несколько литографий, которые принесли ему известность как художнику-иллюзионисту. Одна из его самых известных работ «Относительность». Эшер изобразил модель «бесконечной лестницы» Пенроузов.

Рождер Пенроуз и его отец Лайонел Пенроуз изобрели лестницу, которая делает поворот на 90 градусов и замыкается. Поэтому человек, если бы ему вздумалось по ней взойти, не смог бы подняться выше. На рисунке ниже видно, что собака и человек стоят на одном уровне, что тоже добавляет рисунку невозможности. Если персонажи пойдут по часовой стрелке, то будут постоянно спускаться, а если против часовой — подниматься.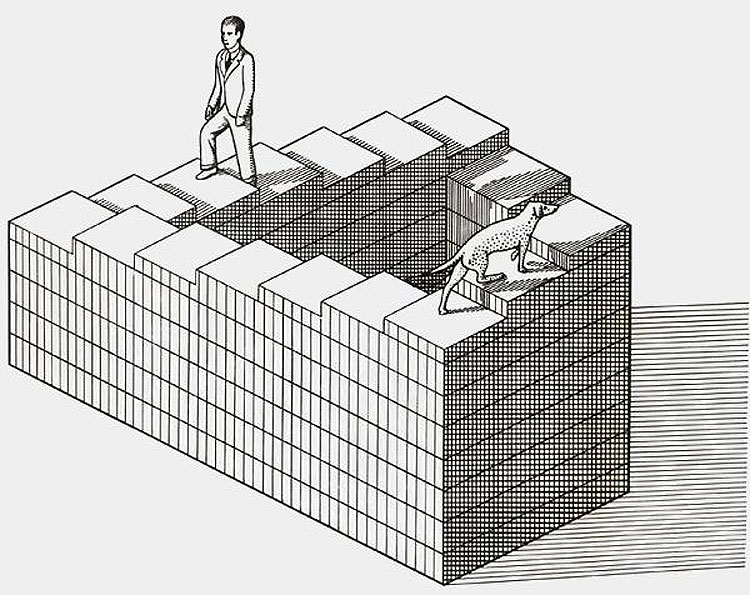

Нельзя не отметить невозможный куб Эшера, который кажется невозможным, потому что человеческому глазу свойственно воспринимать двумерные изображения как трёхмерные объекты (подробнее об Эшере можно почитать здесь).

А также классический пример невозможной фигуры — Трезубец. Он представляет собой фигуру с тремя круглыми зубцами на одном конце и прямоугольными — на другом. Такой эффект достигается за счет того, что трудно однозначно сказать, где тут передний план, а где задний.

В настоящее время процесс создания невозможных фигур продолжается. Ниже приведены некоторые из них (имя создателя -- под фигурой).

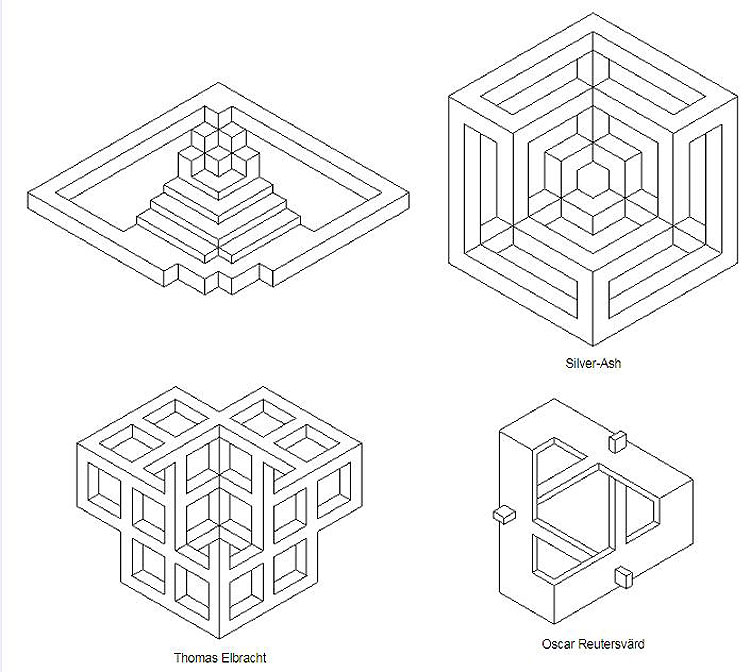
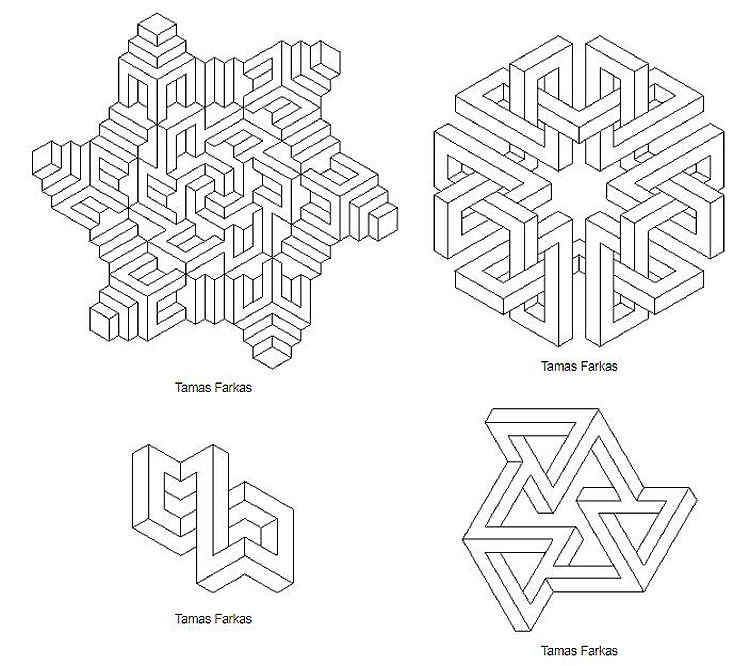
А также невозможно не отметить прекрасные невозможные фигуры, созданные нашим земляком, омичом Анатолием Коненко. Например: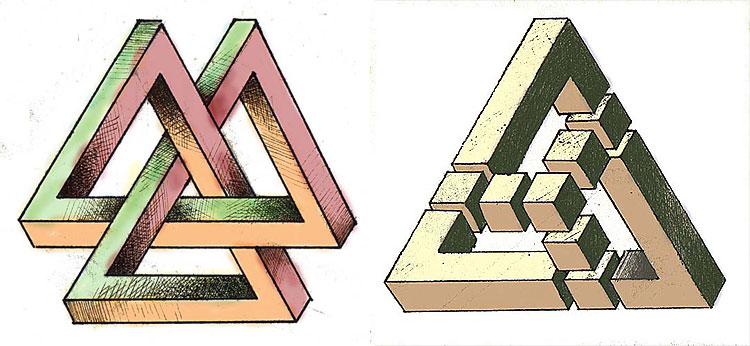

А можно ли увидеть «невозможные фигуры» в реальной жизни?

Многие скажут, что невозможные фигуры действительно нереальны и не могут быть воссозданы. Другие же будут утверждать, что чертеж, изображенный на листе бумаги, является проекцией трехмерной фигуры на плоскость. Следовательно, любая фигура, нарисованная на листе бумаги, должна существовать в трехмерном пространстве. Так кто же прав?

Вторые будут ближе к правильному ответу. Действительно, увидеть «такие» фигуры в реальности можно, необходимо лишь смотреть на них с определенной точки. С помощью картинок ниж , можно убедиться в этом.

Джерри Андрус и его невозможный куб:

Невозможное сцепление шестеренок, тоже воплощенное в реальность Джерри Андрусом.

Скульптура Треугольника Пенроуза (г.Перт, Австралия), все стороны которого перпендикулярны друг другу.

А так скульптура выглядит с другой стороны.

Если вам нравятся невозможные фигуры, можно полюбоваться на них здесь.

Специально для жж матфака Александра Плотникова.

Удивительные фигуры. (Невозможный мир)

Невозможное – это то,
что не может существовать…
или случиться…

Цель урока: развитие объемного видения учащихся; умение объяснить невозможность существования той или иной фигуры с точки зрения геометрии; развитие интереса к предмету.

Оборудование: газета по материалам сайта "Невозможный мир" (Интернет), инструменты для построения фигур, геометрические фигуры, иллюстрации невозможных фигур.

Ход урока:

Вступительное слово:
На протяжении всей истории люди сталкивались с оптическими иллюзиями того или иного рода. Достаточно вспомнить мираж в пустыне, иллюзии создаваемые светом и тенью, а также относительным движением. Широко известен следующий пример: луна, поднимающаяся из-за горизонта, кажется гораздо больше, чем высоко в небе. Все это – лишь несколько любопытных явлений, которые встречаются в природе. Когда эти явления, обманывающие зрение и ум, были впервые замечены, они стали волновать воображения людей.

С давних времен оптические иллюзии использовались, чтобы усилить воздействие произведений искусства или улучшить внешний вид архитектурных творений. Древние греки прибегали к оптическим иллюзиям, чтобы довести до совершенства внешний вид своих великих храмов. В эпоху Средневековья смещенную перспективу иногда использовали в живописи. Позднее многие другие иллюзии использовались в графике. Среди них единственный в своем роде и относительно новый вид оптической иллюзии известен как "невозможные объекты".

Одним из важных навыков для людей, работающих в технической сфере, является способность воспринимать трехмерные объекты в двухмерной плоскости. "Невозможные объекты" построены на использовании трюков с перспективой и глубиной в рамках двухмерного пространства. Невозможные в реальном трехмерном пространстве, они действуют на наше зрение, благодаря смещенной перспективе, манипуляциям с глубиной и плоскостью, обманчивым оптическим намекам, несоответствиям планов, игре света и тени, неясным соединениям, благодаря неправильным и противоречивым направлениям и связям, измененным точкам кода и другим "фокусам", к которым прибегает художник-график.

Намеренное использование невозможных объектов в дизайне встречалось еще в древние времена до появления классической перспективы. Художники пытались найти новые решения. Примером может служить датируемое XV веком изображение Благовещения на фреске собора Св. Марии в голландском городе Бреда. На картине изображен архангел Гавриил, приносящий Марии весть о ее будущем Сыне. Фреска обрамлена двумя арками, поддерживаемыми, в свою очередь тремя колоннами. Однако следует обратить внимание на среднюю колонну. В отличие от других, она исчезает на заднем плане за плитой. С практической точки зрения, художник использовал эту "невозможность" как особую технику, позволяющую избежать разделения сцены на две половины.

Пример такой арки приведен на рис. 1

"Невозможные фигуры" делятся на 4 группы. Попробуем сейчас разобрать основные фигуры из каждой группы. Итак, первая:

Ученик 1:

Удивительный треугольник – трибар.

 

Эта – фигура – возможно первый опубликованный в печати невозможный объект. Она появилась в 1958 году. Её авторы, отец и сын Лайонелл и Роджер Пенроузы, генетик и математик соответственно, определили этот объект как "трехмерную прямоугольную структуру". Она также получила название "трибар".

Определите, что с точки зрения геометрии невозможно.

(С первого взгляда трибар кажется просто изображением равностороннего треугольника. Но стороны, сходящиеся вверху рисунка, кажутся перпендикулярными. В тоже время левая и правая грани внизу тоже кажутся перпендикулярными. Если смотреть на каждую деталь отдельно, то она кажется реальной, но в общем эта фигура существовать не может. Она не деформирована, но при черчении были неправильно соединены правильные элементы.)

Вот еще несколько примеров невозможных фигур на основе трибара. Постарайтесь объяснить их невозможность.

 

Тройной деформированный трибар

 

Треугольник из 12 кубов

Крылатый трибар

Тройное домино

Ученик 2:

Бесконечная лестница

Эту фигуру чаще всего называют "Бесконечной лестницей", "Вечной лестницей" или "Лестницей Пенроуза" – по имени ее создателя. Ее также называют "непрерывно восходящей и нисходящей тропой".

Впервые эта фигура была опубликована в 1958 году. Перед нами предстает лестница, ведущая, казалось бы, вверх или вниз, но при этом, человек, шагающий по ней, не поднимается и не опускается. Завершив свой визуальный маршрут, он окажется в начале пути.

"Бесконечной лестницей" с успехом воспользовался художник Мауриц К. Эшер, на этот раз в своей литографии "Восхождение и нисхождение", созданной в 1960 году.

Лестница с четырьмя или семью ступеньками.

 

На создание этой фигуры с большим количеством ступенек автора могла вдохновить куча обыкновенных железнодорожных шпал. Собравшись взобраться на эту лестницу, вы будете стоять перед выбором: подняться ли по четырем или по семи ступенькам.

Попробуйте объяснить, какими свойствами пользовались создатели этой лестницы.

(Создатели этой лестницы воспользовались параллельными линиями при разработке конечных деталей блоков, находящихся на одинаковом расстоянии; кажется, что некоторые блоки перекручиваются, чтобы соответствовать иллюзии).

Предлагается посмотреть еще одну фигуру. Ступенчатая стена.

Ученик 3:

Следующая группа фигур под общим названием "Космическая вилка". С этой фигурой мы входим в самую сердцевину и суть невозможного. Может быть, это самый многочисленный класс невозможных объектов.

 

Этот пресловутый невозможный объект с тремя (или с двумя?) зубцами стал популярен у инженеров и любителей головоломок в 1964 году. Первая публикация, посвященная необычной фигуре, появилась в декабре 1964 года. Автор назвал ее "Скобой, состоящей из трех элементов". Восприятие и разрешение (если это только возможно) несоответствия в этом новом типе двусмысленной фигуры требует настоящего сдвига зрительной фиксации. С практической точки зрения этот странный трезубец или механизм в виде скобы, абсолютно неприменим. Некоторые называют его просто "досадной ошибкой". Один из представителей аэрокосмической промышленности предложил использовать его свойства при конструировании межпространственного космического камертона.

 

Башня с четырьмя колоннами-близнецами.

Impossible Geometric Shapes In Linear Outline Stock Vector

Другие стоковые иллюстрации

Невозможные знаки устанавливают контур. Линейные бесконечные формы. Невозможные геометрические фигуры. Оптическая иллюзия. Треугольник, Бесконечность

Невозможные знаки устанавливают контур. Линейные бесконечные формы. Невозможные геометрические фигуры.

Геометрический бесшовный узор из невозможных фигур

3d иллюзия невозможных треугольников бесшовный фон фон.

Набор иконок плоской линии геометрических фигур. Топология фигуры сфера, тор, лента Мебиуса, бутылка Клейна векторные иллюстрации

Набор векторных невозможных геометрических фигур

Нереально невозможная геометрическая фигура, элемент вектора

Буквы невозможной геометрии. Невозможный шрифт формы.Геометрическая изометрическая графика. Черные буквы на белом фоне

Сердце абстрактной невозможной геометрической формы на День святого Валентина векторные иллюстрации

Набор затемненных невозможных геометрических объектов

Буквы невозможной геометрии. Невозможный шрифт формы. Низкополигональные 3d персонажи.

Логотип Мебиуса.Невозможная геометрическая форма с тенью на разных фонах. UI, значок сети.

Невозможный 3D объект. Геометрический 3D блок. Оптическая иллюзия. Векторная иллюстрация.

Набор векторных искусства линии невозможной геометрической формы

.

букв невозможной геометрии. Невозможный шрифт формы. Векторного

Дизайнеры также выбрали эти стоковые иллюстрации

Невозможный набор шрифтов

Шестигранный алфавит

Набор невозможных фигур, штрихи нераскрытые

Невозможный шрифт формы

Невозможный шрифт формы

Невозможный шрифт формы

Парадокс невозможных форм, трехмерные скрученные объекты, векторные математические символы

Невозможные формы тонкая линия набор минимальных векторных иконок

Невозможный куб.Линейный дизайн

Буквы невозможной геометрии. Невозможный шрифт формы.

Буквы невозможной геометрии. Невозможный шрифт формы. Низкополигональные 3d персонажи.

Невозможная линия куба 3D-числа

Невозможная ретро линия 3D шрифт ABC

буквы в стиле Мемфис.Цветные буквы в стиле 80-х. Набор векторных букв, построенный на базе

.