Начертить звезду пятиконечную: 7 способов нарисовать пятиконечную звезду

Звезда к Дню Победы

Всем привет и с Праздником Великой Победы!
Неожиданно для себя, очень захотелось что-либо сделать руками, в честь 75-летия Победы в Великой Отечественной Войне. Просто для себя и для родных, вложив в поделку уважение, душу и память к тем, кто жил и победил, вопреки всему, в то тяжелое время. Решил изготовить большую звезду.

Как начертить правильную пятиконечную звезду я забыл, но, как всегда, помог интернет. В принципе достаточно только этих двух картинок (взято тут):

Решено было сделать звезду с высотой луча в 40см, для этого нужно было начертить пару окружностей, отмерить углы и изготовить шаблон.
В качестве материала для шаблона была взята попавшаяся под руку картонка. Особого времени не было, т.к. идея самоделки посетила за день до Праздника, поэтому делал разметку, в общем-то, почти «на глазок». Разметил сектора большой и малой окружности, достаточные для изготовления одного луча, отложил углы 36° и 72 с помощью такой штуки:

Всех с Праздником!!! Ура!!!

Эта загадочная пентаграмма | Статья в журнале «Юный ученый»

В статье раскрывается понятие пентаграммы (пятиконечной звезды). Дается история ее возникновения, основные свойства пентаграммы и способы построения. Исследуются области ее применения, в частности, прогнозирование погоды. Рассматривается методика прогнозирования погоды. Делается вывод о том, что точный долгосрочный прогноз погоды — это реально.

Данная статья являет собой начало большого проекта по созданию долгосрочного прогноза погоды для Республики Алтай. Проект рассчитан на период 2016–2021 гг. и предполагает ряд последовательных работ:

1.                Пятиконечная звезда или пентаграмма.
2.                Семиконечная звезда.
3.                Шестиконечная звезда Давида.
4.                Численные методы, числовые ряды и их расчет.
5.                Построение долгосрочного прогноза погоды.

Все работы будут сопоставляться с уже имеющимися научными трудами. Исследования данного направления предполагают взаимосвязь таких наук, как математика, астрономия, физика, информатика. При этом будут использоваться народные приметы «старины», проводиться исследования погоды на всем временном интервале.

Итак, первая научно-исследовательская работа готова.

Цель работы: исследовать понятие, историю возникновения пентаграммы, способы ее построения и варианты применения.

Для достижения поставленной цели определим задачи работы:

–                    узнать, что такое пентаграмма;

–                    познакомиться с ее историей;

–                    научиться рисовать пентаграмму, строить звездчатые многогранники;

–                    выявить взаимосвязь пентаграммы с прогнозом погоды;

–                    провести необходимые исследования, измерения; сделать выводы.

1.                Что такое пентаграмма

Пентаграмма или пятиконечная звезда (по-другому, пентальфа, пентакл, пентагерон) — она известная даже детям.

Пентаграмма — это правильный пятиугольник. На сторонах этого пятиугольника имеются равнобедренные треугольники одинаковой величины.

Рис. 1. Пятиконечная звезда

Слово «Пентаграмма» в переводе с греческого означает «пять линий» («pente» — пять и «gramma» — черта, линия).

2.                История возникновения пентаграммы

Изображения пентаграммы впервые были найдены на развалинах древнего города Урука. Рисунки эти относятся примерно к 3500 г. до н. э.

Константин I — римский император в свое время принял христианство. Пентаграмма изображалась на его печати. Император даже поместил пятиконечную звезду и на свой амулет, тем самым обретя чистую (истинную) веру.

Родственник (племянник) Короля Артура — английский воин взял изображение пентаграммы за основу и поместил его на своем щите. Этот символ имел статус личного. Каждый из пяти «лучей» пятиконечной звезды относились к определенным достоинствам рыцарей таких, как — «благородство, вежливость, целомудрие, отвага и благочестие».

Существует некоторое учение, где исследуются формы Пространства и закономерности развития Вселенной. Такое учение называется сакральной геометрией. Здесь пентаграмма является ключевой фигурой. Символ пентаграммы известен большинству народов Земли.

В раннем христианстве пентаграмму соотносили с Христом, а именно — его ранами. Пять лучей звезды — пять ран Христа: рана на лбу от тернового венка, раны на руках и раны на ногах. Христос тем самым искупил людские грехи. Также в христианстве пятиконечная звезда является символом Святой Троицы и отождествляет Двойную природу Христа — Божественную и человеческую.

Неземной силой наделяли пентаграмму. «Фигура должна быть совершенно замкнутой и не обнаруживать никаких разрывов» — так говорилось в трагедии «Фауст» немецкого поэта Гёте. Здесь был описан случай, что на доме ученого Фауста пентаграмма была плохо начерчена, потому в его жилище смог проникнуть дьявол Мефистофель.

Сегодня никто не знает наверняка, каким же образом появился и стал использоваться символ пентаграммы. Однако, существует мнение, что этот символ появился во времена жрецов и магов Месопотамии при наблюдении за движением планеты Венера. Наблюдая с Земли за движением Венеры, астрологи выяснили, что Венера за восемь лет проходит все знаки зодиака. При этом она «заворачивает» пять раз по своей траектории. Когда древние астрологи нарисовали классический астрологический круг со знаками зодиака и отметили на нем все эти «завороты», а затем соединили их, то получили точную пентаграмму.

Древние цивилизации приписывали пентаграмме двойной смысл. С одной стороны, этот символ был сильнейшим помощником и защитником, его изображали на амулетах, дверях, одежде и культовых предметах. С другой стороны, пентаграмма считалась символом тайной власти и могущества. Еще один смысл приобрела пентаграмма в письменности Древнего Египта — ее символ использовался как иероглиф и обозначал «обучение».

Большую роль сыграла пентаграмма в учении Пифагора. Он определил, что этот символ содержит золотое сечение. Пифагор сделал вывод, что пентаграмма является геометрическим воплощением математического совершенства. Последователи Пифагора назвали пентаграмму Гигиея по имени древнегреческой богини здоровья и использовали ее для восстановление телесно-духовной гармонии и совершенства. В Пифагорейской школе пентаграмма говорила о пяти годах молчания перед просвещением. При этом была представлена концепция о пяти элементах — огонь, земля, вода, воздух и эфир, которые расположены на лучах пятиконечной звезды. Пифагорейцы считали, что каждая из пяти стихий имеет свое значение, а углы пентаграммы являются воплощением этих стихий:

–                    нижний левый угол звезды означает Землю, физическую выносливость и стабильность;

–                    нижний правый угол символизирует Огонь, смелость и храбрость;

–                    верхний правый угол означает Воду, это проявление интуиции и эмоций;

–                    верхний левый считается стихией Воздуха, он отвечает за искусство и интеллект;

–                    а самая верхняя точка является символом Духа, нашего духовного Я.

В древней Индии и Китае пентаграмму стали использовать независимо от остальных цивилизаций. В VI до н. э. в Китае возникла концепция У-син, которая предполагает «пять движений» или «пять превращений». Эта концепция была своеобразным продолжением течения Инь-Ян. По свидетельствам У-син к пяти элементам гармонии относятся Огонь, Земля, Металл, Вода и Дерево. При взаимодействии эти стихии образует пентаграмму. Эта схема легла в основу древнекитайской философии, традиционной медицины, широко использовалась в нумерологии, гадательных практиках, предсказаниях и боевых искусствах.

Рис. 2. Пентаграмма и стихии

Пентаграмма была и еврейским символом, отражающим священное Пятикнижие, полученное Моисеем от Бога. Пятиконечная Звезда с Полумесяцем является символом ислама и символизирует пять основных столпов этой религии, пять молитв, произносимых ежедневно.

Одним из направлений использования пентаграммы является окультно-религиозный, к которым модно относятся ордена — гностики, масоны, розенкрейцеры, мартинисты и.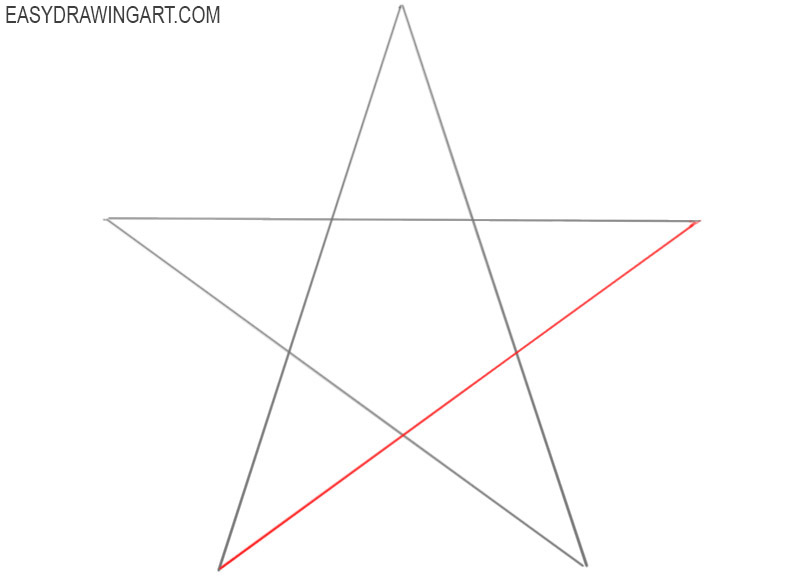  т.д.

В настоящее время пентаграмма — это один из самых часто используемых знаков, который можно встретить везде.

3.                Построение пентаграммы

Пентаграмма — простейшая форма звезды, которую можно изобразить, ни разу не оторвав карандаш от бумаги и при этом ни разу же не пройдя дважды по одной и той же линии. Пентаграмму можно начертить 10 различными способами. Но самые распространенные следующие два: с помощью пятиугольника и транспортира.

Способ построения с помощью правильного пятиугольника изобрел немецкий живописец и график Альбрехт Дюрер.

Необходимо начертить окружность с центром в точке О и с горизонтальным диаметром удобного размера. Через точку О необходимо восстановить перпендикуляр к имеющемуся диаметру. Нижнюю точку обозначить за М.

Затем разделим радиус, идущий от точки О влево, пополам и поставить точку А.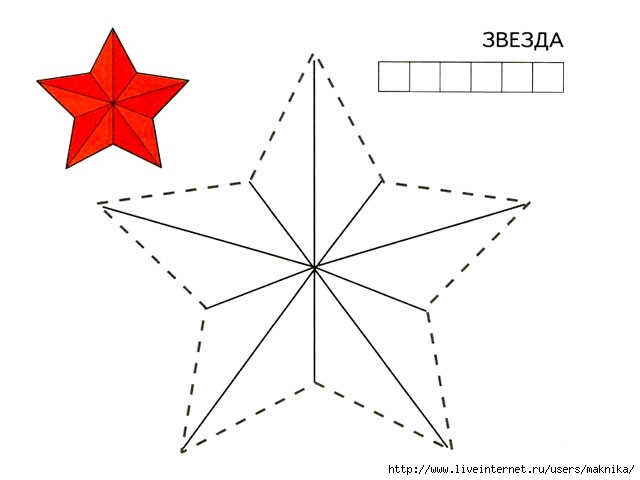 С помощью циркуля, раствор которого равен отрезку АМ, начертить дугу от точки М со второй половиной горизонтального радиуса. Поставить точку N. Аналогично, начертить дугу раствором циркуля, равным отрезку АN и поставить точку К.

Провести окружность с радиусом, равным АК, точки пересечения ее с первой окружностью, обозначить за С и D.

Далее начертить окружности равного радиуса СА из точек С и D. Точки пересечения с основной окружностью отметить и соединить вершины полученных лучей пунктиром. Результатом будет правильный пятиугольник.

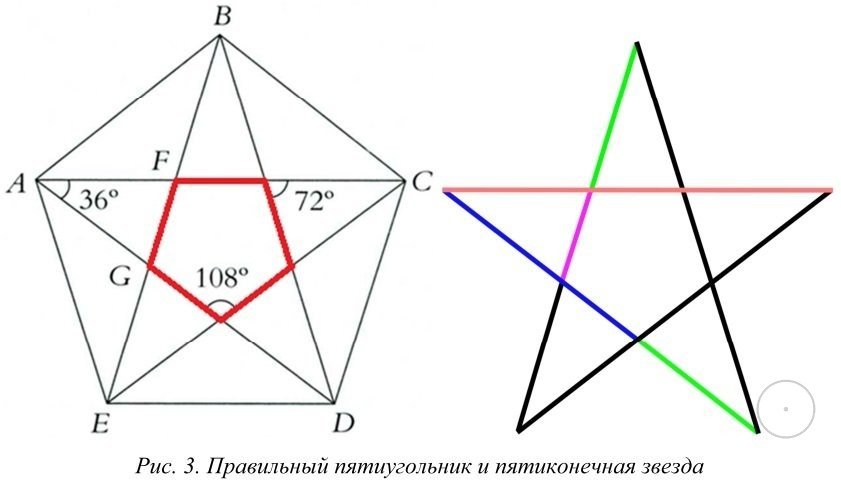
В правильный пятиугольник вписать окружность. Затем провести перпендикуляры к точкам касания сторон пятиугольника с вписанной окружностью. От точек пересечения отметить одинаковые расстояния, поставить точки и соединить их с вершинами (рис.3-а). Осталось обвести звезду ярким цветом, а лишние линии удалить.

Рис. 3. Построение пентаграммы с помощью а) правильного пятиугольника; б) с помощью транспортира

Для того чтобы построить пентаграмму с помощью транспортира, надо через точку О провести любую линию. Построить от этой линии угол 72º и соединить с точкой О. Снова отложить угол такого же размера и так далее. На лучах отметить равные расстояния построить правильный пятиугольник. Определить середины сторон и провести к ним перпендикуляры. На полученных перпендикулярах отложить одинаковые расстояния от центра и соединить полученные точку (рис. 3-б).

4.                Свойства пентаграммы

Пентаграмма обладает интересными геометрическими свойствами:

I свойство. Поворотная симметрия пятого порядка.

В пентаграмме имеется пять осей симметрии. Эти оси совмещаются при повороте на 72º. Яркими примерами поворотной симметрии пятого порядка в живой природе являются следующие: морская звезда, панцирь морского ежа, цветки незабудки, гвоздики, шиповника, яблони, вишни и многих других представителей.

II свойство. Постоянство отношений составляющих её отрезков.

Пентаграмма располагает множеством золотых пропорций.

На рисунке AD: AC = AC: CD = AB: BC = AD: AE = AE: EC

Рис. 4. Пентаграмма — золотая пропорция

Пользуясь симметрией звезды, этот ряд равенств можно продолжить. Все эти отношения равны числу Ф (φ = (1+√5)/2 = 1,618…). Число 1,618034 называется большим числом Фидия и обозначается символом Ф. Число 0,618034 именуется малым числом Фидия и обозначается символом φ.

III свойство. Углы при вершинах пентаграммы равны по 360˚.

Рис. 5. Свойство 3

В пятиугольнике ABCDE <1 = < 2 = < 3 = 108°: 3 = 36°.

Все углы в пентаграмме кратны 36.

IV свойство.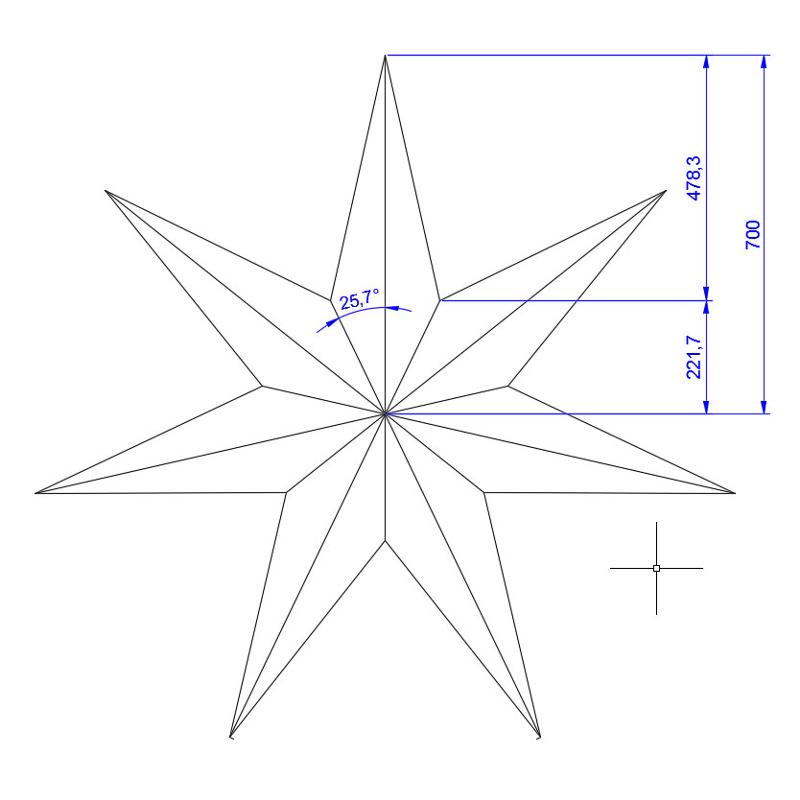 Наличие у пентаграммы возвышенных треугольников.

Лучи пентаграммы, выходящие из одной точки, образуют возвышенный треугольник. Возвышенный треугольник — это равнобедренный треугольник, у которого углы при основании (72°) в два раза больше угла при вершине (36°).

V свойство. Отрезки пентаграммы связаны между собой всеми видами средних линий.

VI свойство. Сумма углов пятиконечной звезды равна 180º.

Приведем доказательство данного свойства:

1, 2, 3, 4, 5 — острые углы звезды.

А, В, С, D, Е — углы пятиугольника внутри звезды

Доказать: 1 + 2 + 3 + 4 + 5 = 180 º

Доказательство.

Как сумма углов треугольника

1 + 4 + B = 180 º, 1 + 3 + D = 180 º,

2 + 4 + E = 180 º, 2 + 5 + C = 180 º, 3 + 5 + A = 180 º.

Сложим равенства и получим:

2 × (1 + 2 + 3 + 4 + 5) + (А + С + В + D + Е) = 900 º,

Откуда 2 × (1 + 2 + 3 + 4 + 5) = 900 º — (А + С + В + D + Е),

где А + В + D + Е + С — сумма углов выпуклого пятиугольника внутри звезды.

Сумма углов выпуклого пятиугольника равна 540 º.

Тогда имеем 1 + 2 + 3 + 4 + 5 = (90: 2) = 360 º: 2 =180 º.

Что и требовалось доказать.

Свойства пентаграммы используются также для построения правильных выпуклых звёздчатых многогранников.

5.                Звездчатые многогранники

Существует всего четыре правильных звездчатых многогранника.

Впервые такие многогранники были открыты И. Кеплером (1571–1630) — первые два. Остальные два многогранника открыл французский математик и механик Луи (1777–1859). Отсюда правильные звездчатые многогранники и стали называться телами Кеплера — Пуансо. Развертки этих тел являются «золотыми» треугольниками, т. е. равнобедренными треугольниками с углами 36, 72, 72 и 108, 36, 36 градусов. При этом отношение их боковой стороны к основанию приближенно равно числу Ф.

Тела Кеплера — Пуансо:

1.                Малый звездчатый додекаэдр

Для построения необходимо сделать трафарет — равнобедренный треугольник с углами 72°, 72° и 36°. Если склеить пять таких треугольников, то получится часть модели, примыкающую к любой вершине.

Рис. 6. Малый звездчатый додекаэдр и его развертка

2.                Большой додекаэдр

Большой додекаэдр состоит из 12 пересекающихся пятиугольных граней. Для построения такой модели необходим трафарет — равнобедренный треугольник с углами 36°, 36° и 108°.

Необходимо соединить полученные заготовки между собой, чтобы получились 20 треугольных пирамид (вершинами вниз), затем склеить пирамиды вместе.

Рис. 7. Большой додекаэдр и его развертка

3.                Большой звездчатый додекаэдр

В качестве трафарета необходимо использовать равнобедренные треугольники с углами 36°, 72° и 72° — лучи пятиконечной звезды.

Рис. 8. Большой звездчатый додекаэдр и его развертка

6.                Применение пентаграммы в прогнозировании погоды

Прогноз погоды, особенно долгосрочный (на несколько недель, месяцев и даже лет) способны рассчитать только профессиональные метеорологи с использованием компьютерных программ. Называется такой прогноз численным.

Численный прогноз погоды используетматематическую модель атмосферы. Первые попытки использовать математические модели для прогнозирования погоды были сделаны в 20-х годах XX века, но только тогда стало это возможным, когда появились компьютеры и компьютерное моделирование. Данный процесс связан с обработкой огромного набора данных и выполнением сложных вычислений и может быть осуществлен только на мощных суперкомпьютерах.

Численные методы впервые стали использоваться для прогнозирования погоды в 1922 году британским математиком Льюисом Фрай Ричардсоном. Однако Ричардсон потерпел неудачу.

Первый успешный прогноз погоды был произведен в 1950 году командой американских метеорологов — Жюлем Чарни (англ.), Филипом Томсоном, Ларри Гейтсом, норвежцем Рагнаром Фьюртофтом (англ.) и математиком Джоном фон Нейманом с использованием супер-ЭВМ. Они использовали упрощенные модели атмосферных потоков на основе сложных уравнений.

Осуществление численного прогнозирования погоды в постоянном режиме началось в США в 1955 году.

Численная модель прогнозирования погоды — это компьютерная программа, построенная на основе физической системы уравнений и составляющая на основе текущих данных метеорологический прогноз. Эта модель может быть глобальной, покрывающей всю Землю, или локальной, покрывающей отдельный участок планеты.

В основе модели лежат математические уравнения, описывающие динамические процессы в атмосфере и связывающие такие параметры как плотность, скорость, давление и температуру. Эти уравнения являются нелинейными и не имеют точного решения, поэтому для их решения используются численные методы. В качестве исходных данных для моделей используются данные зондов, метеоспутников и наземных метеостанций.

Данная модель прогнозирования практически перечеркнула народные приметы, ссылаясь на их темноту и гадательный характер. Однако прежде люди могли достаточно точно предсказывать погоду по различным приметам.

Признанным считается расчет долгосрочного прогноза погоды Якова Брюса (русский государственный деятель, военный, дипломат, инженер и учёный, один из ближайших сподвижников Петра I) по числовым рядам с использованием примет простого народа о погоде. Рассматривая приметы простого народа о погоде, Яков Брюс произвел их цифровую обработку, тем самым с успехом составил долгосрочный прогноз погоды.

Этот же способ был подтвержден Константином Феофилактовичем Агринским. На основе расчетов, сделанных по приметам, Агринский построил свою знаменитую температурную кривую. Однако все эти расчеты были утеряны, как говорят ученые.

Секрет кривой Агринского был раскрыт, спустя 30 лет работы, Леонидом Ивановичем Горбанем — известным предсказателем погоды и природных аномалий.

Л. И. Горбань разгадал секреты Я. Брюса и К. Ф.  Агринского и сделал расчеты долгосрочного прогноза погоды до 2030 года, которые ведутся по числовым рядам планет и народным приметам. Сбываемость прогнозов Л. Горбаня составляет 92–94 %.

Планетный расчет долгосрочного прогноза погоды основывается на знаниях астрономии и движениях планет и их влиянии на погоду Земли.

Рассмотрим пятиконечную звезду (пентаграмму) с числовым рядом планеты Венера. Выше уже говорилось о том, что Венера описывает правильную пентаграмму каждые восемь лет, а если точнее, за 7,9933 года. Значение этого числа непонятно, хотя можно предполагать наличие его связи с числами золотой пропорции или числами, названными именем древнегреческого архитектора Фидия. Это должно быть так, потому что пентаграмма связана с числами 1,618034 и 0,618034. Число 1,618034 называется большим числом Фидия и обозначается символом Ф. Число 0,618034 именуется малым числом Фидия и обозначается символом φ.

Такие числовые ряды имеются у каждой из семи планет Солнечной системы Солнца, Луны, Меркурия, Венеры, Марса, Сатурна, Юпитера [2, с. 8]. Самые древние записи об этих числовых рядах были найдены в Китае. У православных и католиков ведется по ним расчет праздников.

Расчет числовых рядов по пентаграмме — это одна из основ настоящего календаря, который разделен на священные и гражданские годы. Такое разделение можно встретить у самых разных народов: Греции, Египта, Вавилона, Ирана, Тибета, Китая, Индии, Бирмы [2, с. 8]. Священные годы использовались для предсказаний, а гражданские — для простолюдинов.

Далее, на основе расчета по пентаграмме, используется семиконечная звезда («Семиконечная печать Соломона») — по числу дней в недели и шестиконечная звезда (Звезда Давида или Гекзамерон Вечности) — по времени.

Таким образом, календарь-прогноз Горбаня — это таблица из колонок:

1)                 Пентаграмма — расчет по числовым рядам планет;

2)                 Семиконечная звезда — расчет по дням недели;

3)                 Гексарион Вечности — расчет по времени;

4)                 Фаза Луны, которая разделена ещё на колонки:

а)      расчет по фазам Луны и его дням — числовой ряд пентаграммы;

б)     прохождение Луны по знакам Зодиака по каждому дню;

5)                 Церковный календарь, народные приметы.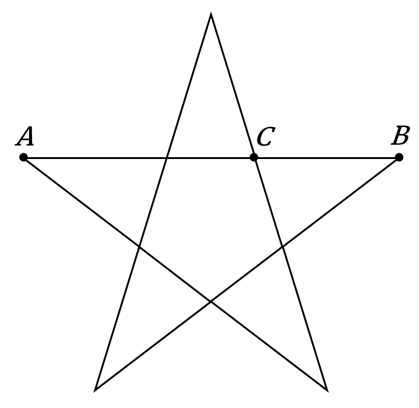

Данные расчеты с долгосрочным прогнозом погоды Горбань проводил в основном для Украины, Киева и Москвы. Все его расчеты держатся в тайне, и нет подлинным данных его способов прогнозирования.

«Когда я понял, что бессмысленно доказывать свою методу в научных кругах потому, что у них одна была цель — узнать секреты любым способом, я начал отдавать свои расчеты работникам сельского хозяйства» [2, с. 10] — говорит Леонид Горбань в одной из последних своих книг.

7.                Исследование погоды

Произведем расчет погодных условий в городе Горно-Алтайске. Для этого составим таблицу (упрощенная модель таблицы Л.Горбаня), соберем свой собственный барометр из подручных материалов. В таблице представлен период с 01.10.2016 года по 28.02.2017 года. Здесь имеются столбцы с показаниями барометра, сайта прогноз погоды, народные приметы, реальные показания термометра «за окном».

Показания снимались в районе МБОУ «СОШ № 13 г. Горно-Алтайска» и в районе остановки «Оптовая база». Так как самодельный барометр может прогнозировать температуру всего за несколько часов, то показания снимались утром, а данные погодных условий по интернет — ссылкам и реальные данные в обеденный период. Данные в сети интернет имели усредненный характер, т. е. средние показатели по отдельным районам города.

Барометр был изготовлен из стеклянной банки, воздушного шарика и трубочки для коктейля. На банку надели шарик, закрепили резинкой. К «макушке» шарика приклеили трубочку. Рядом изготовили «шкалу».

Спустя некоторое время зафиксировали деление: давление, равное 739 мм.рт.ст. с опорой на данные метеорологов.

В результате можно сделать вывод, что при снижении давления происходит потепление, а при повышении — значительное похолодание. Это хорошо видно по диаграммам, представленным в Приложении 2.

Данные исследования представлены в (Приложении 1). При этом можно наблюдать, что во время новолуния и убывающей Луны, температура воздуха значительно ниже, чем во время полнолуния и растущей Луны. А ещё наблюдения привели к выводу, что в районе Оптовой базы г. Горно-Алтайска температура ниже среднего значения по городу на 2–5º.

Зима 2016–2017 гг. выдалась очень снежной, что предсказывал Л. Горбань в своем календаре. В 2016 год господствовала планета Марс по вечному календарю по методике Я.Брюса (Приложение 3).

Рассмотрим предсказания Горбаня для России в целом.

Октябрь. 1–4 ясно, тепло, 5–6 дождь, 7–12 переменно- пасмурно, но тепло, с 15 похолодание, 14–16 дождь, 17–21 ясно, тепло, 22–23 холодно, дождь, с 27 и до конца месяца, холодно, дожди.

Ноябрь. 1–6 холодно, сыро, 1, 3–4 дожди, 7–10 ясно, тепло, 8–13 дождь, мокрый снег, 13–17 оттепель, 18–24 дождь, мокрый снег, снег, с 23 и до конца месяца мороз.

Декабрь. Начинается морозами, которые длятся до 20 числа, снег 4–6, 9- 10 снег, 13–15 снег, 20 снег, 20–24 оттепель, с 25 и до конца месяца мороз, 26–27 снег, 30–31 снег.

В 2017 году господствовало Солнце.

Январь: 1–2 слабые морозы, 5–6 дождь, мокрый снег, с 7.01.05 г. и до конца месяца — морозы, 8–9 — снег, 18–20 — снег, 24–25 — снег, 29–31 — снег.

Февраль: Весь месяц морозы, которые то ослабевают, то усиливаются; 3–5 сильные морозы, 6–8 слабые морозы, 9–11 сильные морозы, 12–14 слабые морозы, 15–25 сильные морозы, 26–28 — слабые морозы, 1 -2 — снег, 5–9 — снег, 12–15 — снег, 18 — снег.

В общем, были предсказаны по всей территории России обильные снегопады. В качестве народных примет возьмем доступные нам приметы: по дыму, по поведению птиц. Мы всю зиму подкармливаем птиц (в основном это воробьи и сороки). А зимой они помогают нам бороться с огородными вредителями. Я заметила, что если наши воробьи стрекочут, прыгают с ветки на ветку, то «идёт» теплая погода. И действительно, несколько дней тепло. Но если их не видно — попрятались, то будет похолодание. Если воробьи сидят тихо на ветках и не резвятся, даже не чирикают, то пойдет снег. Если дрова в печи трещат, то это к морозу, а если печка плохо топится, то — к теплу. А ещё у нас можно наблюдать по дыму из трубы, когда топиться печь. Если дым стоит высоко, то это к морозу. Если дым стелется, значит, давление снижено, и скоро жди потепления, возможно даже с осадками.

Заключение

В процессе работы я познакомилась с понятием «Золотое сечение», увидела золотое сечение, скрытое в пентаграмме. Используя свойства золотого сечения, научилась правильно строить пентаграмму. Были изучены геометрические свойства пентаграммы, найдены связи звезды с окружающим миром. Основная часть работы посвящалась исследованию пентаграммы как геометрической фигуры, а также одного из областей ее применения (прогнозирование погоды).

Данная работа является первым шагом, так как она не закончена. Результат: планирую в следующем году провести изучение семиконечной звезды и шестиконечной звезды Давида, все данные свести в виде собственной книги по прогнозированию погоды на долгие годы для Республики Алтай.

Хочу разгадать секреты предсказания Л.Горбаня по пятиконечной звезде с использованием знаний по астрономии, и ее связи с информатикой, физикой, народными приметами, а главное — математикой. А сегодня мне не хватает знаний по математике.

Поставленные на данном этапе задачи были решены, а, значит, цель работы достигнута.

Как нарисовать идеальную пятиконечную звезду?

Нарисовать идеальную пятиконечную звезду относительно просто, и это можно сделать за несколько простых шагов.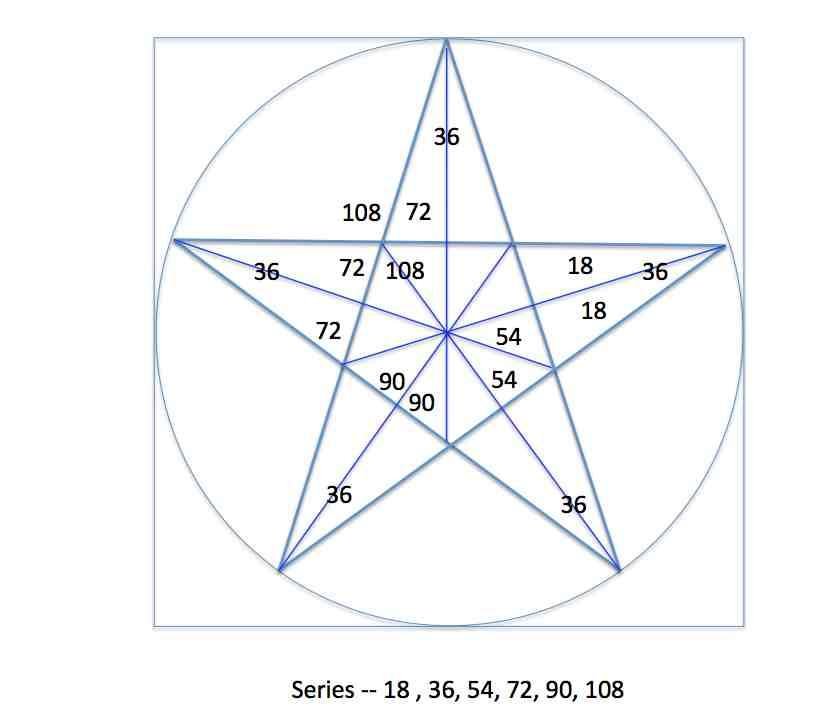

Первый шаг — нарисовать круг. Это можно сделать, обведя предмет, например чашку, или рисуя циркулем. Если у вас есть бумага с линиями сетки, вы также можете использовать линии сетки, чтобы нарисовать аккуратный круг.

Второй шаг — провести пять радиусов из центра круга. Каждый радиус должен быть одинаковой длины и должен пересекать окружность с равными интервалами. Опять же, использование линейки или линий сетки может помочь обеспечить точность.

Последний шаг — соединить концы каждого радиуса вместе. Начните с первой точки и нарисуйте линию, которая идет к третьей точке, а затем продолжается до пятой точки. Затем нарисуйте еще одну линию от первой точки, которая соединяется с четвертой точкой, а затем со второй точкой.

Наконец, проведите последнюю линию от третьей точки к пятой, а затем обратно ко второй точке.

Если все сделано правильно, конечным результатом должна стать идеальная 5-балльная звезда.

Содержание

Какие углы у пятиконечной звезды?

Углы пятиконечной звезды могут различаться в зависимости от конструкции, но обычно звезда состоит из двух групп углов. Первая группа состоит из четырех углов. Все они одинаковы, и их мера обычно составляет 36 градусов.

Вторая группа углов состоит из пяти углов, каждый из которых имеет размер 72 градуса. Все вместе они составляют 360 градусов, образующих полный круг. Если смотреть на звезду сверху вниз, то углы кажутся острыми, а сбоку они кажутся более изогнутыми и круглыми.

Общее количество углов пятиконечной звезды равно девяти, так как каждая точка имеет две стороны.

Какие углы срезать, чтобы получилась звезда?

Чтобы сделать звезду, вам нужно разрезать 5 углов, образующих форму пятиугольника. Начните с создания плоской поверхности и измерения 5 точек, равноудаленных друг от друга. Используя транспортир и электролобзик, начните резать каждый угол под углом 36°.

Обязательно обрежьте до края. Вам нужно будет сильно надавить на лобзик, чтобы убедиться, что угол правильный. После того, как вы закончите первую сторону, переверните пятиугольник и используйте лобзик, чтобы провести ту же линию на другой стороне пятиугольника.

После того, как линии будут вырезаны, у вас должна получиться идеальная пятиконечная звезда!.

Как рисовать звезды поэтапно?

Шаг 1: Начните с рисования треугольника с тремя прямыми линиями, убедившись, что все три линии пересекаются.

Шаг 2: Нарисуйте еще две линии, выходящие из середины, пересекающиеся с первыми тремя линиями и образующие шестиконечную звезду.

Шаг 3: Нарисуйте круг вокруг звезды, обойдя шесть линий и наложив их друг на друга.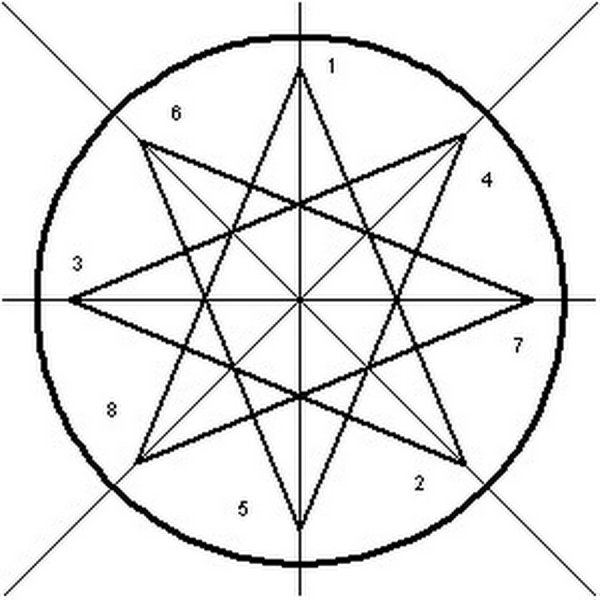

Шаг 4: Добавьте еще два круга, перекрывающих первый и немного ближе к центру.

Шаг 5: Добавьте четвертый круг, перекрывающий три предыдущих и расположенный немного ближе к центру.

Шаг 6: Соедините точки звездочек легкими изгибами, чтобы завершить форму звезды.

Шаг 7: При желании добавьте маленькие линии к вершинам звезд для более сложного вида.

Шаг 8: Вы можете придать своей звезде уникальную текстуру, добавив точки или другие метки на внутренний и внешний круги.

Шаг 9: Раскрасьте звезду, если хотите.

Поздравляем! Теперь вы успешно научились рисовать звезду!

Что я могу использовать, если у меня нет транспортира?

Если у вас нет транспортира, есть несколько альтернатив, которые вы можете использовать для измерения углов. Вы можете попробовать использовать простую линейку или линейку, чтобы оценить угол, если у вас есть твердая рука.

Вы также можете использовать круглый предмет, например скрепку, для оценки угла.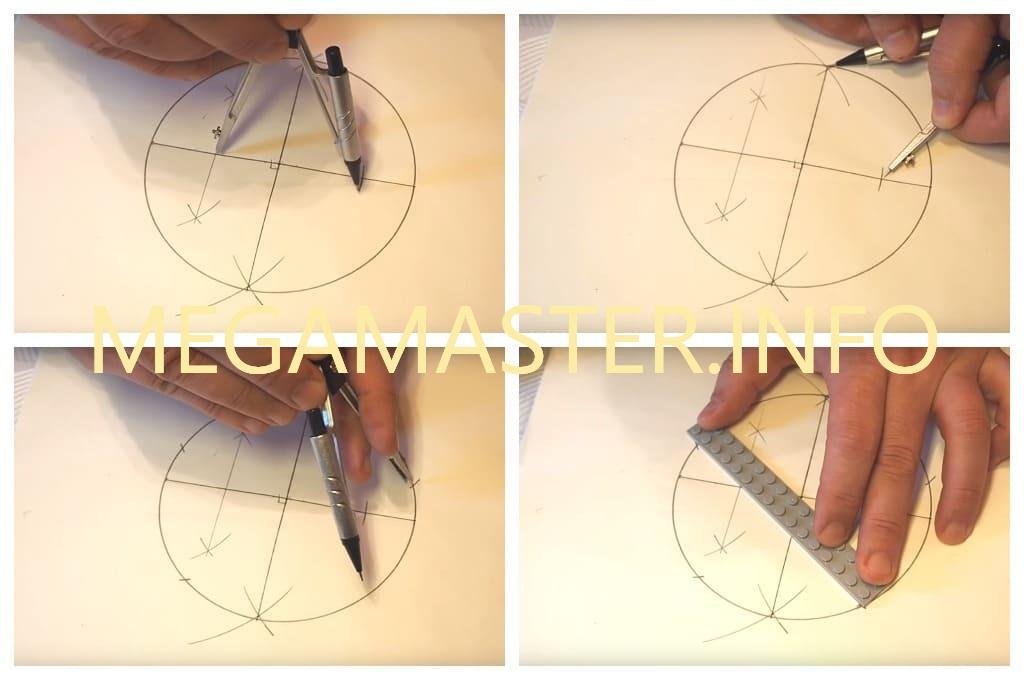 Если у вас есть смартфон, есть несколько доступных приложений, таких как линейка и транспортир, которые виртуально рассчитают ваш угол.

Наконец, если у вас есть некоторые навыки тригонометрии, вы можете использовать лист миллиметровой бумаги, измерительную ленту и калькулятор, чтобы оценить угол линий.

Каким инструментом можно нарисовать звезду?

Звезду можно нарисовать с помощью различных инструментов. Инструменты для рисования, такие как карандаш, ручка, мелок или маркер, можно использовать для рисования звезды.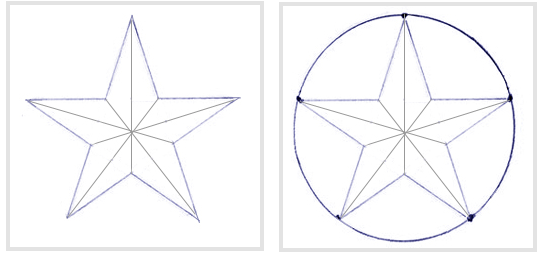 Кроме того, если вы используете компьютерную программу, такую ​​как Adobe Illustrator или Microsoft Paint, вы также можете нарисовать звезду с помощью инструментов, доступных в этих программах.

Кроме того, если вы хотите нарисовать более сложную звезду, вы можете использовать такой инструмент, как циркуль или линейка. Наконец, если у вас есть доступ к 3D-принтеру, вы также можете использовать его для создания формы звезды.

Независимо от того, какой инструмент вы используете, важно иметь хорошее представление об основах геометрии и четкое представление о форме, которую вы хотите создать, прежде чем начать рисовать.

Почему мы рисуем звезду с 5 точками?

Пятиконечная звезда использовалась в качестве символа на протяжении тысячелетий и имеет глубокое значение во многих культурах и религиях. В западном мире звезда ассоциируется с изображением планеты Венера, поэтому ее часто изображают на изображениях богини Афродиты и других связанных с ней божеств.

Пятиконечная звезда также играла важную роль в раннем христианстве, поскольку она была одним из символов, используемых для обозначения Иисуса Христа и его пяти ран.

В более практическом смысле пятиконечная звезда изначально использовалась как символ защиты и руководства. Например, его рисовали на парусах кораблей викингов для безопасного перехода. В Еврейских Писаниях говорится, что каждая из пяти точек представляет одну из пяти книг Торы.

Будучи символом божественного и природного миров, звезда также считается обладающей свойствами руководства, защиты и удачи.

Сегодня пятиконечная звезда по-прежнему используется в популярных рисунках и является напоминанием о древних духовных верованиях. Звезду можно найти в самых разных контекстах: от логотипов с культовым символом звезды, создающим ощущение защиты, до американского флага, на котором изображена звезда для каждого штата.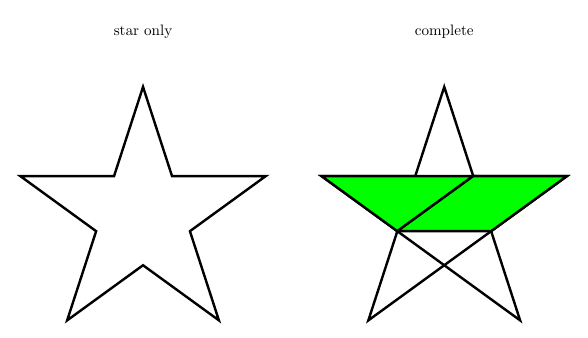

Независимо от контекста, пятиконечная звезда остается мощным символом во всем мире.

python — Графика черепахи, нарисовать звезду?

спросил 8 лет, 4 месяца назад

Изменено 1 год, 1 месяц назад

Просмотрено 82к раз

Я хочу нарисовать заполненную звезду, например:

Пока у меня есть этот код:

 def draw_star(size,color):
    количество = 0
    угол = 144
    в то время как количество <= 5:
        черепаха.вперед(размер)
        черепаха.правый(угол)
        количество += 1
    возвращаться
draw_star(100,"фиолетовый")
 

Я хочу заполнить звезду любым цветом, переданным функцией. Как я могу это сделать?

• питон
• рисунок черепахи

1

Чтобы получить пятиконечную звезду, нужно провести по 2 линии с каждой стороны. Углы нужно добавить к 72 (360/5)

 импортной черепахе
def draw_star (размер, цвет):
    угол = 120
    черепаха.fillcolor(цвет)
    черепаха.begin_fill()
    для стороны в диапазоне (5):
        черепаха.вперед(размер)
        черепаха.правый(угол)
        черепаха.вперед(размер)
        черепаха.право(72 - угол)
    черепаха.end_fill()
    возвращаться
draw_star(100, "фиолетовый")
 

Поэкспериментируйте с различными значениями угла , чтобы получить желаемую форму

2

Найдите «заливку» в документации черепахи:

 def draw_star(size,color):
    количество = 0
    угол = 144
    черепаха.fillcolor(цвет)
    черепаха.begin_fill()
    для _ в диапазоне (5):
        черепаха.вперед(размер)
        черепаха.правый(угол)
    черепаха.end_fill()
draw_star(100,"фиолетовый")
 

Н.Б. возвращает был излишним, и, закодировав цикл таким образом, он не будет рисовать контур дважды.

1

 по определению draw_star (размер, цвет):
...: черепаха.сброс()
...: черепаха.цвет(цвет)
...: черепаха.fillcolor(цвет)
...: черепаха.begin_fill()
...: черепаха.lt(260)
...: для _ в диапазоне (5):
...: черепаха.fd(размер)
...: черепаха.lt(170)
...: черепаха.fd(размер)
...: черепаха.rt(100)
...: черепаха.end_fill()
...:
...:draw_star(размер, цвет)
 

1

Эксперимент с Turtle.fill . Однако, если вы просто используете это в своем коде без дальнейших изменений, вы получите «чередующуюся» заливку:

. между двумя углами) или заполнить внутреннюю часть звезды отдельно (обводя вписанный многоугольник).

5

 def create_star (указатель, color_mix, central_point_x_value,\
                    Central_point_y_value, длина, высота):
    travel_distance = длина * . 223
    pointer.home() # сбрасывает ориентацию указателя
    # без сброса всего
    указатель.penup()
    pointer.goto(central_point_x_value,central_point_y_value)
    указатель.влево(90)
    pointer.forward(height) # перейти к вершине звезды
    pointer.left(18) # должен выпрямить направление в соответствии с потребностями итерации
    #рисуем звезду , идя против часовой стрелки
    # начиная сверху и заканчивая вершиной каждого внешнего треугольника
    указатель.penddown()
    указатель.fillcolor(color_mix)
    указатель.begin_fill()
    количество = 5
    в то время как количество != 0:
        #нарисуй звезду
        указатель.влево(144)
        pointer.forward(путешествие_расстояние)
        указатель.право(72)
        pointer.forward(путешествие_расстояние)
        количество -=1
    указатель.end_fill()
 

1

Если вы работаете в Windows, вам, вероятно, сойдет с рук:

 черепаха.цвет("фиолетовый")
черепаха. begin_fill()
черепаха.круг (100, степень = 720, шаги = 5)
черепаха.end_fill()
 

Однако у этого кода есть две проблемы: это не та звезда в стиле , что и на вашей иллюстрации; это не работает одинаково во всех реализациях Python черепахи/tkinter (некоторые показывают только частичное заполнение):

Вот альтернативная реализация с использованием , штамповка вместо , рисунок , который должен исправить обе проблемы:

 STAR_SIZE = 100
РАСШИРЕНИЕ = 1,2
ПЕРЕВОД = STAR_SIZE * РАСШИРЕНИЕ / 4
черепаха.hideturtle()
черепаха.цвет("фиолетовый")
черепаха.форма("треугольник")
черепаха.turtlesize(STAR_SIZE * РАСШИРЕНИЕ/20)
для _ в диапазоне (5):
    черепаха.право(72)
    черепаха.вперед(ПЕРЕВОД)
    черепаха.штамп()
    черепаха.назад(ПЕРЕВОД)
 

Я сделал это быстро, это можно легко исправить. Не стесняйтесь комментировать лучшее решение 🙂

 импортная черепаха
х = черепаха.Черепаха()
х.скорость(0)
 def draw_star (длина, угол):
 for i in range(5): #звезда состоит из 5 сторон
  х. вперед(длина)
  x.right(угол)
для я в диапазоне (1):
 x.color("purple") #если вам нужен контур звезды, выберите .color("purple" + "outline color")
 x.begin_fill()
 draw_star(100, 144) #144 — идеальный угол для звезды
 х.end_fill()
 

Попробуйте так:

 черепаха.write("★", font=("Arial", 40, "нормальный"))
 

Это просто запись в черепаху, так что это может не помочь, но вы можете попробовать.

 из импорта черепах *
скрыть черепаху ()
def draw_star (размер стороны, точки, альфа-угол, цвет):
    бетаугол = 360/баллы+альфаугол
    цвет заливки (цвет)
    begin_fill()
    для x в диапазоне (точки * 2):
        вперед (в сторону)
        если х% 2 == 0:
            слева (180-альфа-угол)
        еще:
            вправо(180-бетаугол)
    end_fill()
draw_star (70, 8, 90, «серый»)
draw_star(90, 5, 72, 'желтый')
draw_star (120, 5, 36, «красный»)
draw_star(65, 6, 60, "темно-синий")
draw_star(80, 4, 45, 'темно-фиолетовый')
draw_star(80, 3, 30, 'зелено-желтый')
выход по клику()
 

Это должно работать, не стесняйтесь задавать любые вопросы!

 по определению draw_star (размер, цвет):
 количество = 0
 угол = 144
 черепаха.