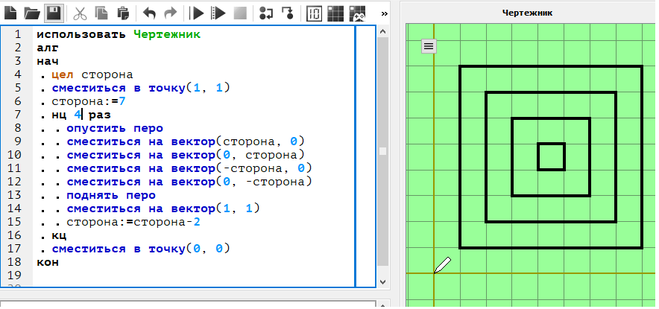
Квадрат как начертить: Как с помощью циркуля построить квадрат?

Содержание

Как построить правильный квадрат вписанный в окружность

Вписать квадрат в окружность легко можно с помощью чертежных инструментов. Но эта задача решается даже при полном их отсутствии. Необходимо только помнить некоторые свойства квадрата.

Вам понадобится

-циркуль
-карандаш
-угольник
-ножницы

Инструкция

Нарисуйте эскиз к задаче. Очевидно, что диаметр окружности является диагональю вписанного в эту окружность квадрата. Вспомните известное свойство квадрата: его диагонали взаимно перпендикулярны. Используйте эту взаимосвязь диагоналей при построении заданного квадрата.

Начертите в окружности диаметр. Из центра с помощью угольника проведите второй диаметр под углом 90 градусов к первому. Соедините точки пересечения перпендикулярных диаметров с окружностью и получите вписанный в эту окружность квадрат.

Если из чертежных инструментов у вас имеется только циркуль, начертите окружность. Отметьте на окружности произвольную точку и проведите через нее диаметр с помощью любого предмета с ровным краем. Теперь нужно с помощью циркуля разделить половину окружности между концами диаметра на две равные части. Из точек пересечения диаметра с окружностью сделайте две засечки, сохраняя неизменным раствор циркуля. Через точку пересечения этих засечек и центр окружности проведите второй диаметр. Очевидно, что он будет перпендикулярен первому.

Если чертежных инструментов у вас нет, можно ножницами вырезать из бумаги круг, ограниченный заданной окружностью. Сложите вырезанную фигуру точно пополам. Повторите операцию. Нужно совместить концы линии сгиба, тогда криволинейные участки совпадут без дополнительных усилий. Зафиксируйте линии сложения. Теперь разверните круг. Линии сгибов отчетливо видны. Загните сегменты круга между точками пересечения линий сгибов с окружностью и отрежьте эти сегменты. Линии отреза являются сторонами искомого квадрата. Поместите вырезанный квадрат в заданную окружность, совместив ее центр с точкой пересечения линий сгиба круга. Вершины квадрата окажутся лежащими на окружности, что и требовалось выполнить.

Вам понадобится

-циркуль
-карандаш
-угольник
-ножницы

Инструкция

Теперь нужно с помощью циркуля разделить половину окружности между концами диаметра на две равные части. Из точек пересечения диаметра с окружностью сделайте две засечки, сохраняя неизменным раствор циркуля. Через точку пересечения этих засечек и центр окружности проведите второй диаметр. Очевидно, что он будет перпендикулярен первому.

Внимание, только СЕГОДНЯ!

Все интересное

Окружность — замкнутая кривая линия, все точки которой находятся на равном расстоянии от одной точки. Эта точка — центр окружности, а отрезок между точкой на кривой и ее центром называется радиусом окружности. Инструкция 1Если через центр…

Окружность называется вписанной в многоугольник, если она полностью размещается внутри этого многоугольника. Каждая сторона описанной фигуры имеет с окружностью общую точку. Вам понадобится-циркуль-карандаш-линейка-лист бумагиИнструкция 1Для…

Деление окружности на пять равных частей – достаточно простая процедура при знании некоторых хитрых приемов, позволяющих сделать это безупречно точно. С этой задачей справиться очень легко, вооружившись циркулем или транспортиром. Вам…

Согласно определению, если все вершины многоугольника принадлежат окружности, он называется «вписанным». Построить на бумаге такую фигуру несложно, особенно если все составляющие ее стороны имеют одинаковую длину. Для правильного…

При проведении построений различных геометрических фигур иногда требуется определить их характеристики: длину, ширину, высоту и так далее. Если речь идет о круге или окружности, то часто приходится определять их диаметр. Диаметр представляет собой…

Задача вписать в окружность многоугольник нередко может поставить взрослого человека в тупик. Ребенку-школьнику необходимо объяснить ее решение, поэтому родители отправляются в серфинг по всемирной паутине в поисках решения. Инструкция …

Деление окружности на несколько равных частей — часто встречающаяся задача. Так можно построить правильный многоугольник, начертить звезду или подготовить основу для схемы. Есть несколько способов решения этой интересной задачи. Вам понадобится-…

Многоугольник называют вписанным, если все его вершины лежат на окружности. Вписать в окружность можно любой правильный многоугольник, в том числе и тот, у которого пять сторон. В классическом черчении для этого требуются некоторые дополнительные…

С построением вписанных и описанных многоугольников постоянно сталкиваются представители самых разных профессий. Обычно никаких проблем не вызывают треугольники, поскольку вписать в окружность можно любую фигуру этого типа. С четырехугольниками дело…

Длину окружности невозможно точно измерить линейкой, а потому ее деление на равные части является непростой задачей, особенно, если этих частей нечетное количество. Деление круга на пять частей осуществляется с помощью обычного циркуля или…

Являющиеся одной из неотъемлемых частей школьной программы, геометрические задачи на построение правильных многоугольников достаточно тривиальны. Как правило, построение ведется путем вписывания многоугольника в окружность, которая вычерчивается…

Данная статья, расскажет вам, о том как при помощи “Vesica Piscis” нарисовать квадрат. В принципе, способ настолько прост, что посвящать этому отдельную статью, возможно и не стоило, но целостность изложения не предполагает пробелов, а по сему, извольте…

Итак, чтобы построить квадрат, вписанный в круг, мы строим “Vesica Piscis” (рис 1).

1. Строим перпендикуляры “Vesica Piscis” АВ и CD (рис 1). А и В – центры исходных окружностей, С и D – точки их пересечения. Отмечаем точку пересечения перпендикуляров АВ и СD, точку О.

2. Строим окружность вписанную в “Vesica Piscis” , с центром в точке О и радиусом равным половине радиуса любой из исходных окружностей, например АО.

3. Отмечаем точки пересечения перпендикуляра СD и вписанной окружности (с центром О, радиусом АО), точки F и E.

4. Проводим прямые АF и AE (рис 2).

5. Отмечаем точки пересечения прямых АF, AE с исходной окружностью (с центром А, радиусом АВ), точки G,H,K,L .

6. Проводим прямые GL, LK, KH, HG (рис 3).

7. Квадрат GHKL, вписанный в исходную окружность (с центром А, радиусом АВ) построен.

Наверное, совсем не лишним, будет напомнить, основные свойства квадрата.

Итак.

1. Стороны, квадрата, равны.

2. Внутренние углы, квадрата, прямые (90 0).

3. Диагонали, квадрата, равны.

4. Диагонали, квадрата, являются биссектрисами его углов.

5. Диагонали, квадрата, перпендикулярны между собой.

6. Диагонали, квадрата, делят друг друга пополам.

7. Центры вписанного и описанного квадратов совпадают с центром соответствующей окружности.

8. Диагонали вписанного или описанного квадратов делят окружность на четыре равные части.

Ну вот, пожалуй, и все…

python — Как нарисовать квадрат по координатам? Получается нарисовать только две линии

Задать вопрос

Вопрос задан 1 год 11 месяцев назад

Изменён 1 год 11 месяцев назад

Просмотрен 357 раз

import tkinter as tk
import tkinter.messagebox as tkmb
class MyWindow(tk.
  Frame):
    def __init__(self):
       self.root=tk.Tk()
       super().__init__(self.root)
       menu_main=tk.Menu(self.root)
       self.root.config(menu=menu_main)
       menu1=tk.Menu(menu_main)
       menu_main.add_cascade(label="File",menu=menu1)
       menu1.add_command(label="Quit",command=self.ext)
       menu2=tk.Menu(menu_main)
       menu_main.add_cascade(label="Edit",menu=menu2)
       menu2.add_command(label="Input",command=self.inp)
       self.canva=tk.Canvas(self.root,width=600,height=600,bg="white")
       self.canva.pack()
       self.xa=2
       self.ya=0
       self.xb=0
       self.yb=0
       self.xc=0
       self.yc=2
       self.xd=0
       self.yd=0
       self.show()
       self.root.mainloop()
    def show(self):
        self.canva.create_line(self.scale(self.xa),self.scale(self.ya),
                               self.scale(self.xb),self.scale(self.yb))
        self.canva.create_line(self.scale(self.xc),self.scale(self.yc),
                               self.  scale(self.xd),self.scale(self.yd))
        self.canva.create_line(self.scale(self.xa),self.scale(self.ya),
                               self.scale(self.xb),self.scale(self.yd))
        self.canva.create_line(self.scale(self.xb),self.scale(self.yb),
                               self.scale(self.xd),self.scale(self.yd))
    def scale(self,value):
        return 300+60*value
                          
    def ext(self):
       if tkmb.askyesno("Exit","Do you want to exit?"):
           self.root.destroy()
    def inp(self):
        self.root.destroy()        
MyWindow()

python
tkinter

   self.xb=0
   self.yb=0
   ...
   self.xd=0
   self.yd=0

У квадрата все вершины — разные:

   self.xd=2
   self.yd=2

В линиях перепутаны координаты точек.

Зарегистрируйтесь или войдите

Регистрация через Google

Регистрация через Facebook

Регистрация через почту

Отправить без регистрации

Почта

Необходима, но никому не показывается

Отправить без регистрации

Почта

Необходима, но никому не показывается

Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки

Как нарисовать идеальный квадрат (+ распространенные ошибки)

Категории

КатегорииВыберите категориюКниги по искусству и дизайну (7)Учебники по перспективе для начинающих (19)Лучшее из (64)Концепт-арт (28)Творчество (33)Интервью с дизайнерами (26)Цифровой рисунок (55) Приложение Concepts (3) Morpholio Trace ( 1) Photoshop (19) Sketcha (1) Sketchbook Pro (13)Быстрое рисование (4)Мебель (1)Вдохновение (3)УЧИТЬСЯ 1 СОВЕТ В ДЕНЬ (381)Мотивация (100)Руководство по дизайну продукта (56)Школа и карьера ( 57) Дизайн обуви (30) Рисуйте как профессионалы (10) Проблемы с рисованием! (13)Инструменты для рисования (38) Шариковая ручка (22)Учебники по рисованию (147)Программное обеспечение (5)Городские зарисовки (16)Влог (8)

Сегодня мы продолжаем второе видео из серии из 6, иллюстрирующее книгу Designer Starter Kit (не стесняйтесь скачать ее и начать с нее. Это бесплатно.)

ВИДЕО 2/6
Как рисовать идеальный квадрат.

Если вы хорошо справились с предыдущим уроком о том, как сделать прямые линии, этот урок будет для вас намного проще.

Некоторые из вас могут задаться вопросом. Что сложного в том, чтобы нарисовать квадрат? Зачем нам нужен учебник для этого?

Дело в том, что рисовать что угодно (даже простейшее) можно несколькими способами, и так получилось, что одни способы дают больше результата, чем другие. Сохраняйте мышление и получайте более интеллектуальные результаты , в будущем вы получите большую эффективность для более сложных рисунков.

Видеоинструкция на картинках ниже

1- Нарисуйте линию, 2- Нарисуйте ее параллель, 3- Добавьте боковые линии. 4- НЕ пытайтесь угадать каждый угол 90°.

Не забудьте использовать чертеж Призрака

Добавьте квадрат, соединяющий точки.

ТадаА!

У вас есть прекрасное произведение искусства, которое можно повесить на стену 😛 Шучу.

Возьмите несколько листов бумаги и нарисуйте много квадратов разного размера.

СОВЕТ: Можно записать дату, сохранить как архив.
Повторяйте процесс время от времени и следите за своим прогрессом.

Увидимся на видео номер 3, чтобы узнать больше об основах создания эскизов!

Опять же, эти видео связаны со Стартовым набором дизайнера. Чтобы лучше насладиться серией руководств, я рекомендую вам сначала загрузить ее.

основы рисования основы рисования учебник для начинающих основы дизайна эскизов рисовать умнее рисовать квадрат легко как рисовать квадрат как лучше рисовать квадрат идеальный квадрат основы рисования эскиза учебник для начинающих

Chou-Tac

Привет! Я продуктовый дизайнер из Франции.

Если методы рисования, которые я приобрел, помогают мне в жизни и в карьере промышленного дизайнера, я считаю, что они также могут помочь вам достичь своей цели в дизайне как студенту или профессионалу.

Моя цель — помогать вам в ваших дизайнерских проектах и путешествиях!

Оставьте комментарий в блоге или отправьте мне электронное письмо по адресу choutac@thedesignsketchbook.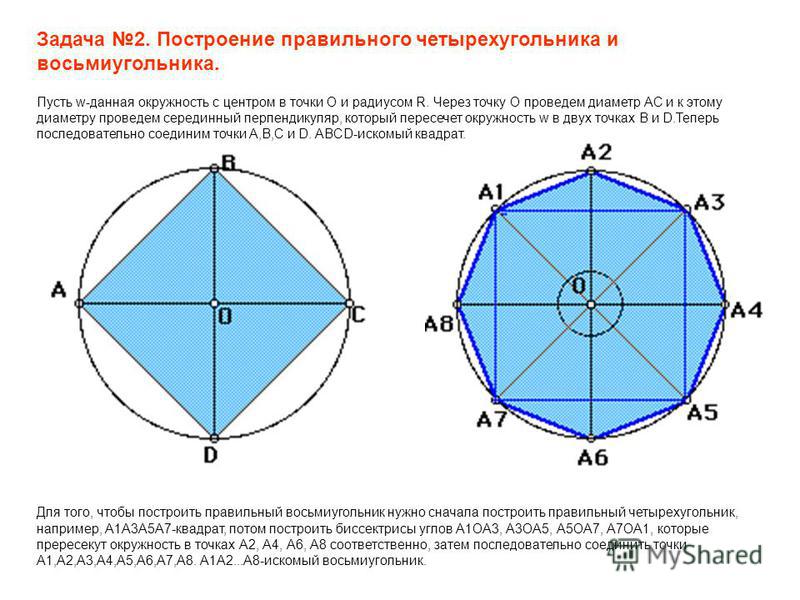 com 🙂

Chou-Tac

Посмотреть все сообщения

Как построить квадрат — 2 метода

Содержание

Этот пост также доступен на: हिन्दी (хинди)

Квадрат — это двумерная замкнутая фигура с четырьмя равными сторонами и четырьмя вершинами. Размер всех четырех углов квадрата равен 9 долларам.{\circ}$, поэтому вы можете нарисовать уникальный квадрат, зная только длину одной стороны квадрата.

Ниже приведены шаги для построения уникального квадрата с заданной стороной.
Шаг 1: Нарисуйте отрезок $\text{AB}$ заданной длины.

Шаг 2: Растяните строку $\text{AB} вправо.

Шаг 3: Установите указатель циркуля на $\text{B}$ и растяните его на любую удобную ширину. Нарисуйте дугу с каждой стороны $\text{B}$ в точках $\text{E}$ и $\text{F}$.

Шаг 4: Установите циркуль в точку $\text{F}$ и любой удобной ширины нарисуйте дугу над точкой $\text{B}$.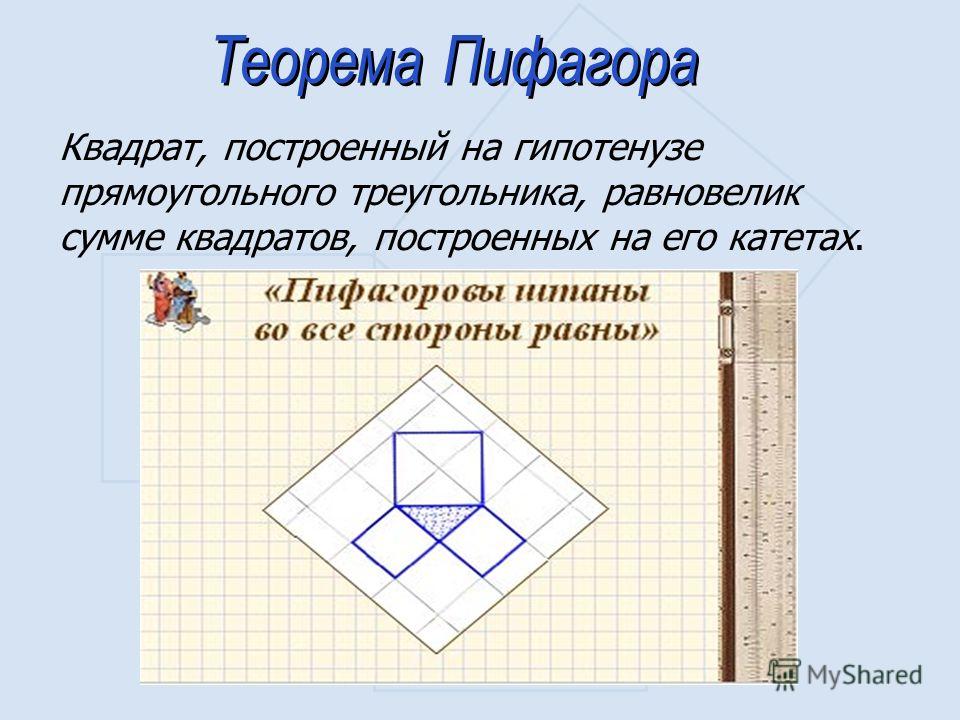

Шаг 5: Не изменяя ширину компаса, поместите циркуль на $\text{G}$ и нарисуйте дугу над $\text{B}$, пересекая предыдущую дугу и создавая точку $\text{ G}$

Шаг 6: Соедините пинты $\text{B}$ через $\text{G}$

Шаг 7: Установите циркуль на $\text{A}$ и установите его ширину в $\text{AB}$. Эта ширина останется неизменной, пока мы создадим три другие стороны квадрата

Шаг 8: Проведите дугу над точкой $\text{A}$.

Шаг 9: Не изменяя ширины, переместите циркуль в точку $\text{B}$. Проведите дугу через $\text{BG}$, создав точку $\text{C}$ – вершину квадрата.

Шаг 10: Не меняя ширины, переместите циркуль в $\text{C}$. Проведите дугу слева от $\text{C}$ через выходящую дугу, создав точку $\text{D}$ – вершину квадрата.

Шаг 11: Соединить точки $\text{C}$, $\text{D}$ и $\text{A}$, $\text{D}$

$\text{ABCD}$ — квадрат, каждая сторона которого имеет длину $\text{AB}$.

СКАЧАТЬ БЕСПЛАТНО КАРТОЧКИ ПО МАТЕМАТИКЕ:

Красиво оформленные карточки для печати, которые помогут вам запомнить все важные математические понятия и формулы.

Как построить квадрат по одной диагонали?

Так как диагонали квадрата равны и перпендикулярны друг другу, а также делят друг друга пополам. Следовательно, зная длину одной из диагоналей квадрата, можно построить уникальный квадрат.

Ниже приведены шаги для построения квадрата с заданной диагональю.

Шаг 1: Постройте линию $\text{AC}$ как заданную диагональ квадрата

Шаг 2: Определите точку $\text{M}$ как середину диагонали $\text{AC }$

Шаг 3: Постройте перпендикуляр в $\text{M}$

Шаг 4: Постройте окружность с центром в $\text{M}$ и радиусом $\text{MC} $

Шаг 5: Назовите точки пересечения между окружностью и перпендикуляром в точке $\text{M}$ как $\text{B}$ и $\text{D}$

Шаг 6: Соедините четыре точки $\text{A}$, $\text{B}$, $\text{C}$ и $\text{D}$, чтобы получить нужный квадрат

Известные математики

Практические задачи

Что такое квадрат в геометрии?
Постройте квадрат со стороной $4 \text{cm}$.
Постройте квадрат с диагональю $6 \text{cm}$.

Часто задаваемые вопросы

Можем ли мы построить квадрат, зная длину его диагонали?

Да, мы можем построить квадрат, если знаем длину его диагонали. Так как диагонали квадрата равны и перпендикулярны друг другу, а также делят друг друга пополам. Следовательно, зная длину одной из диагоналей квадрата, мы можем построить единственный квадрат.

Какой первый шаг в построении квадрата?

Построение квадрата начинается с заданного отрезка $\text{AB}$. Затем он возводит перпендикуляр на одном конце линии, который станет второй стороной квадрата. Затем компас устанавливается на длину данной стороны, а остальные три стороны отмечаются.

Заключение

Квадрат – это четырехугольник со сторонами равной длины и углами одинаковой меры. Существует два способа построения квадрата в зависимости от известного для построения параметра. Вы можете построить квадрат, если известна длина стороны или длина диагонали.

Квадрат как начертить: Как с помощью циркуля построить квадрат?

Как построить правильный квадрат вписанный в окружность

Вам понадобится

Инструкция

Вам понадобится

Инструкция

python — Как нарисовать квадрат по координатам? Получается нарисовать только две линии

Зарегистрируйтесь или войдите

Отправить без регистрации

Отправить без регистрации

Как нарисовать идеальный квадрат (+ распространенные ошибки)

Категории

Chou-Tac

Как построить квадрат — 2 метода

Как построить квадрат по одной диагонали?

Практические задачи

Часто задаваемые вопросы

Можем ли мы построить квадрат, зная длину его диагонали?

Какой первый шаг в построении квадрата?

Заключение

Рекомендуемая литература

Вам также может понравиться

Лучшие ланчбоксы для студентов

Добавить комментарий Отменить ответ