Рисуем куб. | Рисуем вместе
Начнем ab ovo что в нашем случае означает с куба:).
Вы, должно быть, знаете, что традиционно самое первое и самое простое задание по рисунку — это нарисовать куб. Задание действительно самое простое, но уже при его выполнении можно сделать массу ошибок (которые в дальнейшем переползают в более сложные постановки). Поэтому, скучное и неинтересное задание на самом деле очень полезно сделать.
Рисовать разумеется, лучше с натуры, так что, если вы не рисуете куб в учебном заведении, можно его просто склеить из листа ватмана. Оптимальный размер стороны 18-20 см. Готовый кубик нужно поставить на стул или стол, который предварительно можно накрыть темной тканью. Красивые складки выкладывать не обязательно, для начала наша задача разобраться с простой геометрией. Источник света традиционно находится слева и сверху, лучше свет натуральный, то есть от окна. Но лампа тоже сгодится. Осталось выбрать себе место и начать!
На выборе места, кстати, хотелось бы остановиться отдельно. Во-первых, не стоит слишком приближаться. Посмотрите, какого примерно размера то, что вы будете изображать (не сам куб, а все, что попадает в кадр — вместе с краем стола и драпировкой).
Расстояние от изображаемых предметов до художника должно быть в 2-3 раза больше размера этих предметов.
Это справедливо для любой постановки, будь это натюрморт или человек. Объект должен попадать в поле зрения целиком, так, чтобы его увидеть, не приходилось крутить головой. Мольберт или доску нужно поставить также с расчетом на то, что она не будет закрывать обзор. В идеале вы можете видеть рисунок и натюрморт одновременно и только переводите взгляд с одного на другое.
Кроме того, желательно выбрать место так, чтобы вы видели 3 грани кубика (то есть, смотрите на него не в лоб, а сбоку). Боковые грани куба (как и край стола) в рисунке не должны быть параллельны листу — это не слишком хорошо воспринимается в готовой работе.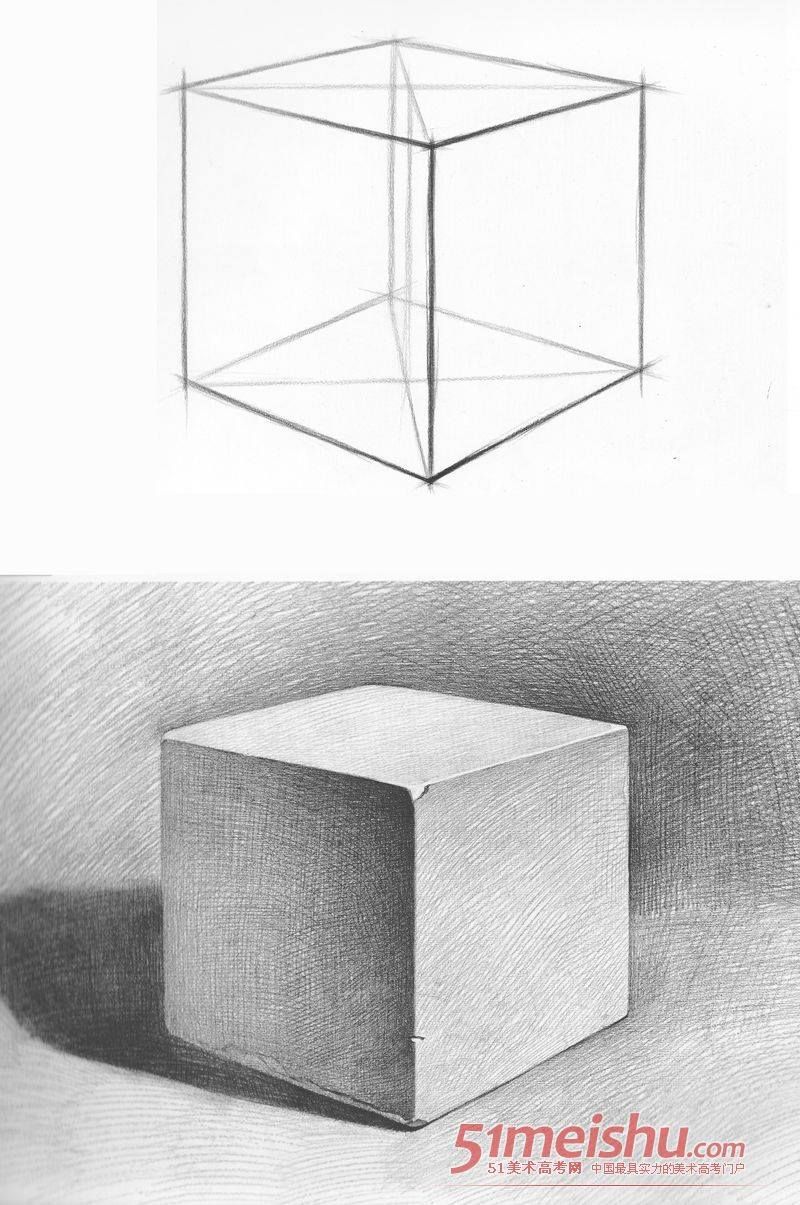
На первом этапе вы просто намечаете положение в листе. В случае с кубом (и любым другим неодушевленным предметом в количестве 1 шт.), вы располагаете его так, чтобы справа и слева расстояние до края листа было одинаковым, а сверху пространства оставалось немного больше, чем снизу. На сколько больше? На глаз. Или читаем про композицию)
Далее, в тонких линиях намечаются грани. Помним про линейную перспективу. Вертикальные линии параллельны друг другу, остальные должны сходиться на горизонте. Линию горизонта найти достаточно просто, она всегда находится на уровне глаз. То есть, высота линии горизонта величина не постоянная и зависит от того, лежите вы, стоите или залезли на стремянку. Не стоит брать слишком высокий или слишком низкий горизонт. В первом случае будет впечатление вывернутости и искаженной перспективы, во втором — верхняя плоскость будет или вообще не видна, или так сильно сократится, что будет трудно ее рисовать.
Не нужно стараться рисовать идеально ровный куб. Мы только намечаем грани, далее линии построения будут уточняться.
Следующий и заключительный этап — светотеневая моделировка. Если вы не уверены в отличном качестве штриха, набирайте тон постепенно, твердым карандашом, постепенно меняя на более мягкие. Не штрихуйте каждую часть отдельно, золотое правило художника — работа на каждом этапе может быть остановлена. То есть, карандаш летает по всему рисунку, тон накладывается равномерно.
Не старайтесь штриховать строго по форме, направление штриховки не так принципиально. На данном этапе ваша задача — набрать тон.
По мере проработки тоном становятся видны ошибки в построении, уточняем направление и положение граней.
Выравниваем тон. Очень полезно по ходу работы отходить и смотреть на рисунок издалека. Так можно заметить ошибки, которые не заметны «в упор». Снова уточняем положение граней куба.
Чтобы работа выглядела выразительней, можно добавить контраста. В рисунке самый яркий контраст лежит там, где предмет приближается. В нашем случае — это ближний к нам угол куба. Вот и все, действительно очень просто.Результат может быть приблизительно такой)
В рисунке самый яркий контраст лежит там, где предмет приближается. В нашем случае — это ближний к нам угол куба. Вот и все, действительно очень просто.Результат может быть приблизительно такой)
Для самопроверки можно провести диагонали куба — как известно, диагонали должны пересечься в одной точке. Для перспективы это правило также справедливо.
Разумеется, все, что написано выше относится не только к рисованию куба. Просто куб — самый подходящий пример для иллюстрации и самый простой предмет в исполнении для начала.
Если получилось, можно переходить к более сложным предметам. Следующая ступень: Рисуем шар.
Содержание
Вернуться на главную страницу
Урок 62. куб — Математика — 4 класс
Урок № 62. Куб
Перечень вопросов, рассматриваемых в теме:
Что такое — куб?
Как распознавать и называть куб, его грани, ребра, вершины.?
Глоссарий по теме:
Куб — это многогранник, поверхность которого состоит из шести квадратов.
Грани куба – это стороны куба, которые представляют собой квадрат.
Ребра куба – это стороны граней куба.
Вершина куба— это точка, где сходятся три грани или точка, в которой сходятся три ребра куба.
Площадь фигуры – это часть плоскости, ограниченная замкнутой ломаной или кривой линией.
Периметр фигуры — это сумма длин всех сторон фигуры.
Основная и дополнительная литература по теме урока:
- Моро М.И., Бантова М.А. и др. Математика 4 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 110
- Математика: Рабочая тетрадь для 4 класса/ О.А. Рыдзе, К.А. Краснянская. – М.; СПб.: Просвещение, 2012. – с. 26-32
Теоретический материал для самостоятельного изучения
Подумайте, на какие две группы можно разделить фигуры?
Верно, на плоские и объемные.
Назовите плоские геометрические фигуры.
Верно, квадрат, треугольник, прямоугольник.
Объемные фигуры называются – геометрическими телами.
Вы видите геометрическое тело «шар» и геометрическое тело «куб».
Внимательно посмотрите и скажите, из какой фигуры состоит поверхность куба?
Верно, поверхность куба состоит из квадратов, их называют гранями куба.
Посчитайте, сколько граней у куба.
Правильно, у куба 6 граней.
Стороны граней (квадратов) называют ребрами куба.
Посчитайте, сколько ребер у куба?
Верно, у куба 12 ребер.
Вершины граней – это вершины куба.
Посчитайте, сколько вершин у куба.
Правильно, у куба 8 (восемь) вершин.
Таким образом, у куба 6 граней, 12 ребер, 8 вершин.
Для того чтобы изготовить модель куба необходимо построить развертку куба.
И какого бы куб ни был роста, сшить костюм для него очень просто. Для начала же, сделав разметку, изготовьте раскройку – развертку. Шесть квадратов! Нехитрое дело. Но расклеить их надо умело.
Куб в жизни человека.
Где можно встретить куб? Здания чаше всего имеют кубическую форму, так что можно просто выглянуть в окно, и вы сразу увидите куб.
Самая знаменитая игрушка-головоломка «кубик-рубик».
Кристаллы поваренной соли имеют форму куба.
Выполним несколько тренировочных заданий.
1. Найдите и напишите номер того куба, который сделан из данной развёртки.
Правильный вариант/варианты (или правильные комбинации вариантов): 4
2. Выберите правильное утверждение.
а) площадь круга больше площади квадрата;
б) площадь круга меньше площади квадрата;
в) площади фигур равны.
Правильные варианты: б) площадь круга меньше площади квадрата.
схема с фото и видео
Гексаэдр или куб – это многогранник, все стороны которого представляют собой квадраты. Любите загадки и головоломки? Эта статья научит вас, как сделать куб из бумаги или картона. Рассмотрим такие необычные изделия, как куб йошимото и куб-трансформер.
Любите загадки и головоломки? Эта статья научит вас, как сделать куб из бумаги или картона. Рассмотрим такие необычные изделия, как куб йошимото и куб-трансформер.
Из развертки
Развертками называют схемы, позволяющие сделать объемную фигуру из бумаги или картона. Для начала научимся строить развертку. Для ее изготовления вам нужна бумага, карандаш, линейка и ножницы.
Все стороны куба представляют собой квадраты. Значит, для начала на листе бумаги нужно начертить квадрат. При этом не забывайте о правилах геометрии – у квадрата все стороны равны, а углы составляют 90°. Далее, вспоминаем, сколько граней у куба – шесть. То есть на схеме для склеивания их тоже должно быть шесть. Вокруг центрального квадрата начертите четыре квадрата. Куда же деть еще один? Просто начертить его сбоку от одного из квадратов. Грани на месте, не хватает припусков для склеивания. Их нужно начертить на трех боковых квадратиках. Составляют они 0,5—1 см.
Не забудьте подрезать их уголки под углом 45°, так они не будут мешаться при склеивании фигуры.
Развертка готова! Вот что у вас должно получиться:
Теперь нужно вооружиться ножницами и клеем и собрать фигуру. Вырежьте развертку при помощи ножниц. Далее, нужно согнуть все грани куба, а также припуски. Смажьте грани клеем и соедините куб воедино. Объемный куб из бумаги готов!
Оригами кубик
Техника оригами очень древняя. Ее появление связано с изготовлением бумаги в Древнем Китае. Ее секрет переняли японцы, именно там и зародилось искусство оригами. Раньше фигурки, сложенные из бумаги, носили сакральный смысл. Ими украшали храмы, свадебные и траурные церемонии. Японцы верили, что подвешенные над головой больного шары, сложенные в технике оригами, помогут отогнать болезнь и злых духов. Позже это искусство стало носить не только религиозный, но и развлекательный характер.
Большинство схем для оригами происходит еще с древних времен, но и современные мастера внесли немалый вклад в развитие этого необычного вида творчества. Предлагаем вам попробовать сложить куб в технике оригами. Для этого нужно взять квадратный лист бумаги и сделать сгиб по центру, а потом согнуть края к середине. Такая начальная фигура называется дверь.
Предлагаем вам попробовать сложить куб в технике оригами. Для этого нужно взять квадратный лист бумаги и сделать сгиб по центру, а потом согнуть края к середине. Такая начальная фигура называется дверь.
Далее, разверните заготовку и согните углы, как показано на схеме:
Сложите края к центру и заправьте верхние и нижние уголки в кармашки:
Переверните заготовку и согните по линиям, указанным на схеме:
Получился модуль. Для сбора кубика таких модулей нужно шесть. В каждой детали есть кармашки, именно в них вставляются соседние модули. Соедините детали по схеме:
Оригами кубик готов. Для красоты можно сделать каждую грань из бумаги разных цветов.
Необычная головоломка
Хотите порадовать любимых деток необычной головоломкой или сделать незабываемый фотоальбом? Тогда вам пригодится небольшой мастер-класс по созданию куба-трансформера. На каждой грани такого кубика можно расположить картинку или фотографию, а внутри еще целых шесть картинок.
Для изготовления такого кубика вам понадобится:
- 12 картинок или фотографий;
- Клей;
- 8 кубиков с гранями по 4 см;
- Скотч.
Кубики можно взять самые обычные детские или склеить самому по такой развертке:
Для начала посмотрите места крепления кубиков:
Важно понимать! Весь секрет трансформаций такой головоломки состоит в правильном склеивании пар кубиков.
Чтобы было более понятно, рассмотрим этот процесс пошагово. Сначала склейте две пары кубиков так, как показано желтыми полосками на схеме:
Расположите эти четыре кубика рядом и склейте в местах, указанных синим цветом:
Поставьте кубики так, как показано на схеме. При этом желтая склейка окажется со стороны противоположной красной. Склейте по красным линиям:
Фото нужно расположить на четверке кубиков. Размер фотографий 8 на 8 см.
Важно приклеить фото аккуратно, особенно, если вы будете делать это при помощи клея. Иначе можно ненароком склеить те грани, которые отвечают за правильную трансформацию головоломки. Так что лучше воспользоваться горячим клеем или двусторонним скотчем.
Необычный фотоальбом из кубика-трансформера готов! Как его можно раскладывать и просматривать картинки, вы можете увидеть на фото:
Японское изобретение
Настоящей головоломкой может стать не только сам куб, изобретенный японским ученым Наоки Йошимото в 1971 году, но и сборка этого необычного изделия. По данной схеме нужно собрать 48 пирамидок.
Как правильно собрать эту чудесную поделку и о ее трансформациях, вы можете наглядно посмотреть в данном видеоуроке:
Видео по теме статьи
Более подробно об изготовлении кубов и головоломок, состоящих из них, вы можете увидеть в предложенной ниже подборке видео. Приятного вам творчества!
youtube.com/embed/AVwrLnMmY5E?feature=oembed» frameborder=»0″ allowfullscreen=»»/>
Как начертить куб в изометрической проекции поэтапно. Прямоугольная изометрия
Для выполнения изометрической проекции любой детали необходимо знать правила построения изометрических проекций плоских и объемных геометрических фигур.
Правила построения изометрических проекций геометрических фигур. Построение любой плоской фигуры следует начинать с проведения осей изометрических проекций.
При построении изометрической проекции квадрата (рис. 109) из точки О по аксонометрическим осям откладывают в обе стороны половину длины стороны квадрата. Через полученные засечки проводят прямые, параллельные осям.
При построении изометрической проекции треугольника (рис. 110) по оси X от точки 0 в обе стороны откладывают отрезки, равные половине стороны треугольника. По оси У от точки О откладывают высоту треугольника. Соединяют полученные засечки отрезками прямых.
Рис. 109. Прямоугольная и изометрические проекции квадрата
Рис. 110. Прямоугольная и изометрические проекции треугольника
При построении изометрической проекции шестиугольника (рис. 111) из точки О по одной из осей откладывают (в обе стороны) радиус описанной окружности, а по другой — H/2. Через полученные засечки проводят прямые, параллельные одной из осей, и на них откладывают длину стороны шестиугольника. Соединяют полученные засечки отрезками прямых.
Рис. 111. Прямоугольная и изометрические проекции шестиугольника
Рис. 112. Прямоугольная и изометрические проекции круга
При построении изометрической проекции круга (рис. 112) из точки О по осям координат откладывают отрезки, равные его радиусу. Через полученные засечки проводят прямые, параллельные осям, получая аксонометрическую проекцию квадрата. Из вершин 1, 3 проводят дуги CD и KL радиусом 3С. Соединяют точки 2 с 4, 3 с С и 3 с D. В пересечениях прямых получаются центры а и б малых дуг, проведя которые получают овал, заменяющий аксонометрическую проекцию круга.
Соединяют точки 2 с 4, 3 с С и 3 с D. В пересечениях прямых получаются центры а и б малых дуг, проведя которые получают овал, заменяющий аксонометрическую проекцию круга.
Используя описанные построения, можно выполнить аксонометрические проекции простых геометрических тел (табл. 10).
10. Изометрические проекции простых геометрических тел
Способы построения изометрической проекции детали:
1. Способ построения изометрической проекции детали от формообразующей грани используется для деталей, форма которых имеет плоскую грань, называемую формообразующей; ширина (толщина) детали на всем протяжении одинакова, на боковых поверхностях отсутствуют пазы, отверстия и другие элементы. Последовательность построения изометрической проекции заключается в следующем:
1) построение осей изометрической проекции;
2) построение изометрической проекции формообразующей грани;
3) построение проекций остальных граней посредством изображения ребер модели;
Рис. 113. Построение изометрической проекции детали, начиная от формообразующей грани
4) обводка изометрической проекции (рис. 113).
- Способ построения изометрической проекции на основе последовательного удаления объемов используется в тех случаях, когда отображаемая форма получена в результате удаления из исходной формы каких-либо объемов (рис. 114).
- Способ построения изометрической проекции на основе последовательного приращения (добавления) объемов применяется для выполнения изометрического изображения детали, форма которой получена из нескольких объемов, соединенных определенным образом друг с другом (рис. 115).
- Комбинированный способ построения изометрической проекции. Изометрическую проекцию детали, форма которой получена в результате сочетания различных способов формообразования, выполняют, используя комбинированный способ построения (рис. 116).
Аксонометрическую проекцию детали можно выполнять с изображением (рис.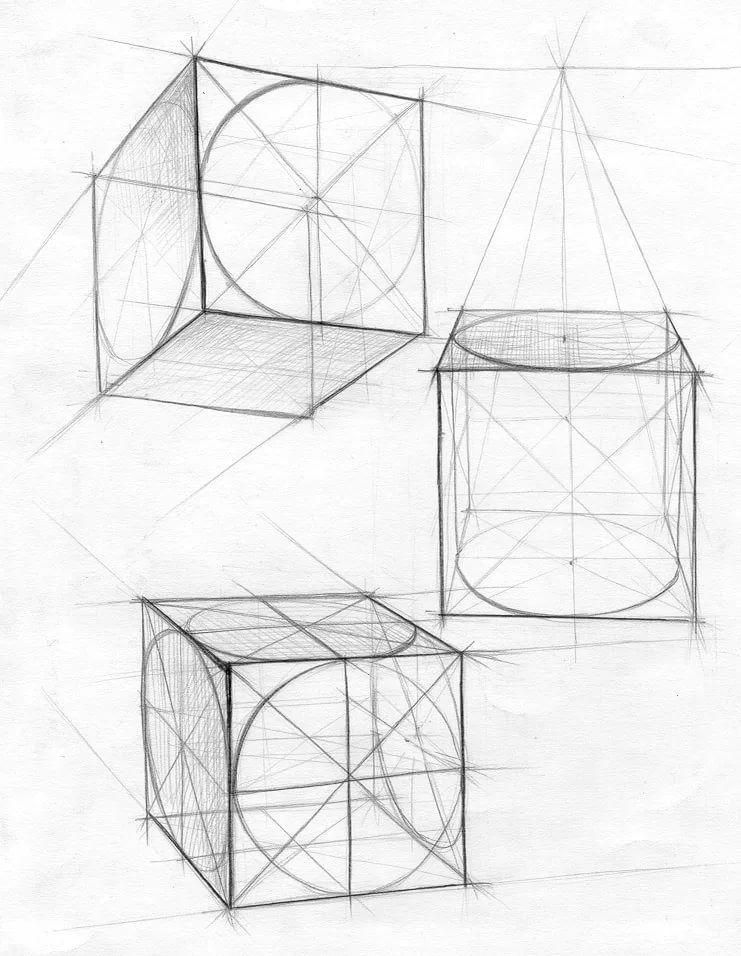 117, а) и без изображения (рис. 117, б) невидимых частей формы.
117, а) и без изображения (рис. 117, б) невидимых частей формы.
Рис. 114. Построение изометрической проекции детали на основе последовательного удаления объемов
Рис. 115 Построение изометрической проекции детали на основе последовательного приращения объемов
Рис. 116. Использование комбинированного способа построения изометрической проекции детали
Рис. 117. Варианты изображения изометрических проекций детали: а — с изображением невидимых частей;
б — без изображения невидимых частей
Рассмотрим, как в изометрической проекции изображаются окружности. Для этого изобразим куб с вписанными в его грани окружностями (рис. 3.16). Окружности, расположенные соответственно в плоскостях, перпендикулярных осям х, у, z, изображаются в изометрии в виде трех одинаковых эллипсов.
Рис. 3.16.
Для упрощения работы эллипсы заменяют овалами, очерчиваемыми дугами окружностей, их строят так (рис. 3.17). Вычерчивают ромб, в который должен вписываться овал, изображающий данную окружность в изометрической проекции. Для этого на осях откладывают от точки О в четырех направлениях отрезки, равные радиусу изображаемой окружности (рис. 3.17, а ). Через полученные точки a, b, с, d проводят прямые, образующие ромб. Его стороны равны диаметру изображаемой окружности.
Рис. 3.17.
Из вершин тупых углов (точек А и В ) описывают между точками а и b, а также с и d дуги радиусом R, равным длине прямых Ва или Вb (рис. 3.17, б ).
Точки С и Д лежащие на пересечении диагонали ромба с прямыми Ва и Вb, являются центрами малых дуг, сопрягающих большие.
Малые дуги описывают радиусом R, равным отрезку Са (Db ).
Рассмотрим построение изометрической проекции детали, два вида которой даны на рис. 3.18, а.
3.18, а.
Построение выполняют в следующем порядке. Сначала вычерчивают исходную форму детали – угольник. Затем строят овалы, изображающие дугу (рис. 3.18, б ) и окружности (рис. 3.18, в).
Рис. 3.18.
Для этого на вертикально расположенной плоскости находят точку О, через которую проводят изометрические оси х и z. Таким построением получают ромб, в который вписана половина овала (рис. 3.18, б ). Овалы на параллельно расположенных плоскостях строят перенесением центров дуг на отрезок, равный расстоянию между данными плоскостями. Двойными кружочками на рис. 3.18 показаны центры этих дуг.
На тех же осях х и z строят ромб со стороной, равной диаметру окружности d. В ромб вписывают овал (рис. 3.18, в).
Находят центр окружности на горизонтально расположенной грани, проводят изометрические оси, строят ромб, в который вписывают овал (рис. 3.18, г ).
Расположение осей диметрической проекции и способ их построения приведены на рис. 3.19. Ось z проводят вертикально, ось х – под углом около 7° к горизонтали, а ось у образует с горизонталью угол приблизительно в 41° (рис. 3.19, а ). Построить оси можно, пользуясь линейкой и циркулем. Для этого из точки О откладывают по горизонтали вправо и влево по восемь равных делений (рис. 3.19, б ). Из крайних точек восставляют перпендикуляры. Высота их равна: для перпендикуляра к оси х – одному делению, для перпендикуляра к оси у – семи делениям. Крайние точки перпендикуляров соединяют с точкой О.
Рис. 3.19.
При вычерчивании диметрической проекции, как и при построении фронтальной, размеры по оси у сокращают в 2 раза, а по осям х и z откладывают без сокращений.
На рис. 3.20 показана диметрическая проекция куба с вписанными в его грани окружностями. Как видно из этого рисунка, окружности в диметрической проекции изображаются эллипсами.
Рис. 3.20.
Технический рисунок – это наглядное изображение, выполненное по правилам аксонометрических проекций от руки, на глаз. Им пользуются в тех случаях, когда нужно быстро и наглядно показать на бумаге форму предмета. Обычно в этом возникает необходимость при конструировании, изобретательстве и рационализации, а также при обучении чтению чертежей, когда с помощью технического рисунка нужно пояснить форму детали, представленной на чертеже.
Выполняя технический рисунок, придерживаются правил построения аксонометрических проекций: под теми же углами располагают оси, так же сокращают размеры по осям, соблюдают форму эллипсов и последовательность построения.
В изометрической проекции все коэффициенты равны между собой:
к = т = п;
3 к 2 = 2,
k = yj 2УЗ — 0,82.
Следовательно, при построении изометрической проекции размеры предмета, откладываемые по аксонометрическим осям, умножают на 0,82. Такой перерасчет размеров неудобен. Поэтому изометрическую проекцию для упрощения, как правило, выполняют без уменьшения размеров (искажения) по осям х, у, I, т.е. принимают приведенный коэффициент искажения равным единице. Получаемое при этом изображение предмета в изометрической проекции имеет несколько большие размеры, чем в действительности. Увеличение в этом случае составляет 22% (выражается числом 1,22 = 1: 0,82).
Каждый отрезок, направленный по осям х, у, z или параллельно им, сохраняет свою величину.
Расположение осей изометрической проекции показано на рис. 6.4. На рис. 6.5 и 6.6 показаны ортогональные (а) и изометрические (б) проекции точки А и отрезка Л В.
Шестигранная призма в изометрии. Построение шестигранной призмы по данному чертежу в системе ортогональных проекций (слева на рис. 6.7) приведено на рис. 6.7. На изометрической оси I откладывают высоту Н, проводят линии, параллельные осям хиу. Отмечают на линии, параллельной оси х, положение точек / и 4.
Отмечают на линии, параллельной оси х, положение точек / и 4.
Для построения точки 2 определяют координаты этой точки на чертеже — х 2 и у 2 и, откладывая эти координаты на аксонометрическом изображении, строят точку 2. Таким же образом строят точки 3, 5 и 6.
Построенные точки верхнего основания соединяют между собой, проводят ребро из точки / до пересечения с осью х, затем —
ребра из точек 2 , 3, 6. Ребра нижнего основания проводят параллельно ребрам верхнего. Построение точки Л, расположенной на боковой грани, по координатам х А (или у А) и 1 А очевидно из
Изометрия окружности. Окружности в изометрии изображаются в виде эллипсов (рис. 6.8) с указанием величин осей эллипсов для приведенных коэффициентов искажения, равных единице.
Большая ось эллипсов расположена под углом 90° для эллипсов, лежащих В ПЛОСКОСТИ хС>1 к ОСИ у, В ПЛОСКОСТИ у01 К ОСИ X, в плоскости хОу К ОСИ?.
При построении изометрического изображения от руки (как рисунка) эллипс выполняют по восьми точкам. Например, лоточкам 1, 2, 3, 4, 5, 6, 7 и 8 (см. рис. 6.8). Точки 1, 2, 3 и 4 находят на соответствующих аксонометрических осях, а точки 5, 6, 7 и 8 строят по величинам соответствующих большой и малой осей элипса. При вычерчивании эллипсы в изометрической проекции можно заменять овалами и строить их следующим образом 1 . Построение показано на рис. 6.8 на примере эллипса, лежащего в плоскости xOz. Из точки / как из центра, делают засечку радиусом R = D на продолжении малой оси эллипса в точке О, (строят также аналогичным образом и симметричную ей точку, которая на чертеже не показана). Из точки О, как из центра проводят дугу CGC радиуса D, которая является одной из дуг, составляющих контур эллипса. Из точки О, как из центра проводят дугу радиуса O^G до пересечения с большой осью эллипса в точках О у Проводя через точки О р 0 3 прямую, находят в пересечении с дугой CGC точку К, которая определяет 0 3 К — величину радиуса замыкающей дуги овала. Точки К являются также точками сопряжения дуг, составляющих овал.
Точки К являются также точками сопряжения дуг, составляющих овал.
Изометрия цилиндра. Изометрическое изображение цилиндра определяется изометрическими изображениями окружностей его основания. Построение в изометрии цилиндра высотой Н по ортогональному чертежу (рис. 6.9, слева) и точки С на его боковой поверхности показано на рис. 6.9, справа.
Предложено Ю.Б. Ивановым.
Пример построения в изометрической проекции круглого фланца с четырьмя цилиндрическими отверстиями и одним треугольным приведен на рис. 6.10. При построении осей цилиндрических отверстий, а также ребер треугольного отверстия использованы их координаты, например координаты х 0 и у 0 .
Для трёхмерных объектов и панорам.
Ограничения аксонометрической проекции
Изометрическая проекция в компьютерных играх и пиксельной графике
Рисунок телевизора в почти-изометрической пиксельной графике. У пиксельного узора видна пропорция 2:1
Примечания
- По ГОСТ 2 .317-69 — Единая система конструкторской документации. Аксонометрические проекции.
- Здесь горизонтальной называется плоскость, перпендикулярная оси Z (которая является прообразом оси Z»).
- Ingrid Carlbom, Joseph Paciorek. Planar Geometric Projections and Viewing Transformations // ACM Computing Surveys (CSUR) : журнал. — ACM , декабрь 1978. — Т. 10. — № 4. — С. 465-502. — ISSN 0360-0300 . — DOI :10.1145/356744.356750
- Jeff Green. GameSpot Preview: Arcanum (англ.) . GameSpot (29 февраля 2000).(недоступная ссылка — история ) Проверено 29 сентября 2008.
- Steve Butts. SimCity 4: Rush Hour Preview (англ.) . IGN (9 сентября 2003). Архивировано
- GDC 2004: The History of Zelda (англ.) . IGN (25 марта 2004). Архивировано из первоисточника 19 февраля 2012. Проверено 29 сентября 2008.
- Dave Greely, Ben Sawyer.
КУБ — это… Что такое КУБ?
куб — куб, а, мн. ч. к уб ы, к уб ов … Русский орфографический словарь
ч. к уб ы, к уб ов … Русский орфографический словарь
КУБ — (лат. cubus). 1) третья степень данной величины. 2) правильный шестигранник, т. е. тело, ограниченное шестью квадратами. 3) снаряд для перегонки жидкостей; то же, что алембик. 4) растение куб (Indigo), из которого добывается кубовая краска.… … Словарь иностранных слов русского языка
куб — 1. КУБ, а; кубы; м. [греч. kybos] 1. Геометрическое тело правильный шестигранник, все грани которого квадраты; предмет, имеющий форму такого шестигранника. Начертить куб. Композиция из гипсовых кубов и призм. Мраморный куб памятника. 2. Разг. =… … Энциклопедический словарь
КУБ — ОАО АКБ «Кузбассугольбанк» http://cbank.ru/ организация, фин., энерг. КУБ кнопочный пост управления взрывобезопасный КУБ ОАО «Кредит Урал банк» http://www.credit … Словарь сокращений и аббревиатур
КУБ — муж. перегонный сосуд, алембик, снаряд для перегонки жидкостей, особ. винных. Куб бывает стекляный, глиняный, медный и пр., разной величины и вида; он наглухо кроется колпаком, и перегонная жидкость идет парами в горло, шейку, а оттуда в… … Толковый словарь Даля
куб — сущ., м., употр. сравн. часто Морфология: (нет) чего? куба, чему? кубу, (вижу) что? куб, чем? кубом, о чём? о кубе; мн. что? кубы и кубы, (нет) чего? кубов и кубов, чему? кубам и кубам, (вижу) что? кубы и кубы, чем? кубами и кубами, о чём? о… … Толковый словарь Дмитриева
кубіт — кубі/т, род. кубіта, мн. кубіти, род. мн. кубітів одиниця інформації, що закодована в квантовій системі, фізичний носій інформації, що може перебуватив станах |0> та |1> і будь якій суперпозиції цих станів. • Стан кубіта може змінюватись… … Фізико-технічний словник-мінімум
КУБ — 1. КУБ1, куба, муж. (греч. kybos). 1. Правильный шестигранник, все грани которого (квадраты (мат. ). Начертить куб. 2. Мера объема, равная кубическому метру. Куб дров. 3. Сосуд для перегонки или кипячения жилкостей в форме шара или цилиндра с… … Толковый словарь Ушакова
). Начертить куб. 2. Мера объема, равная кубическому метру. Куб дров. 3. Сосуд для перегонки или кипячения жилкостей в форме шара или цилиндра с… … Толковый словарь Ушакова
КУБ — (от латинского cubus, от греческого kybos игральная кость), 1) один из 5 типов правильных многогранников, имеющий гранями квадраты, 12 ребер, 8 вершин, в каждой вершине сходятся 3 ребра. Куб иногда называют гексаэдром. 2) Третья степень а3 числа… … Современная энциклопедия
КУБ — КУБ, в математике результат двукратного умножения числа на самого себя. Таким образом, кубом числа а является произведение а х а х а, что записывается как а3. Куб называют также третьей степенью числа. Кубом именуется правильная шестисторонняя… … Научно-технический энциклопедический словарь
Куб и его свойства
На одном из предыдущих занятий мы с вами познакомились с таким многогранником, как прямоугольный параллелепипед.
Решая задачу со спичками, получили геометрическую фигуру, которую называют пирамидой.
Впереди вас ожидает знакомство и с другими многогранниками. А сейчас давайте вернёмся к прямоугольному параллелепипеду.
Итак, поверхность прямоугольного параллелепипеда состоит из 6 прямоугольников. Эти прямоугольники называются гранями параллелепипеда.
Обратите внимание, что два соседних прямоугольника имеют общую сторону, которая называется ребром прямоугольного параллелепипеда. Концы рёбер называются вершинами прямоугольного параллелепипеда.
Таким образом, прямоугольный параллелепипед имеет 6 граней, 12 рёбер и 8 вершин.
Отметим, что при всём различии многогранников поверхность каждого
из них состоит из плоских многоугольников, которые называют гранями
многогранника. Два соседних плоских многоугольника имеют общую сторону – ребро
многогранника. Концы рёбер являются вершинами многогранника.
Этот многогранник называется октаэдром. У него 8 граней, которые являются треугольниками, 12 рёбер и 6 вершин.
Куб – это такой прямоугольный параллелепипед, в котором все рёбра равны между собой. Обратите внимание, что рёбра куба, которые не видны, мы изображаем пунктирными линиями. Это позволяет получить полное представление о фигуре и её расположении по отношению к нам.
Все грани куба – равные между собой квадраты. Поверхность куба состоит из 6 равных квадратов. Посмотрите, что грани, расположенные друг против друга, не имеют общих рёбер. Эти грани называются противоположными.
Грани, которые имеют общее ребро, называются смежными.
А теперь давайте проведём небольшой эксперимент. Возьмём коробку, которая имеет форму куба. Откроем её, потом разрежем по четырём вертикальным рёбрам, а затем развернём.
Фигуру, которая у нас получилась, называют развёрткой куба. Она состоит из 6 равных квадратов.
Следующие фигуры также являются развёртками куба.
С помощью любой из развёрток вы можете изготовить модель куба. Для этого можно поступить следующим образом. Начертить на листе бумаги развёртку куба. Вырезать её. Согнуть по отрезкам, которые соответствуют рёбрам куба, и склеить.
Теперь давайте проведём с вами отрезок, который соединит наиболее удалённые друг от друга вершины куба. Эти вершины называют противоположными.
Отрезок, соединяющий две противоположные вершины куба, называется диагональю куба.
А теперь давайте с вами решим несколько задач.
Задача первая. Определите, какой кубик получится из данной развёртки.
Решение.
Давайте мысленно представим, какие грани кубика являются смежными,
то есть имеют общее ребро, и сравним с предложенными вариантами, чтобы найти
верный. Для этого нам удобнее всего сравнивать грани, которые отличаются по
нанесённому на них рисунку.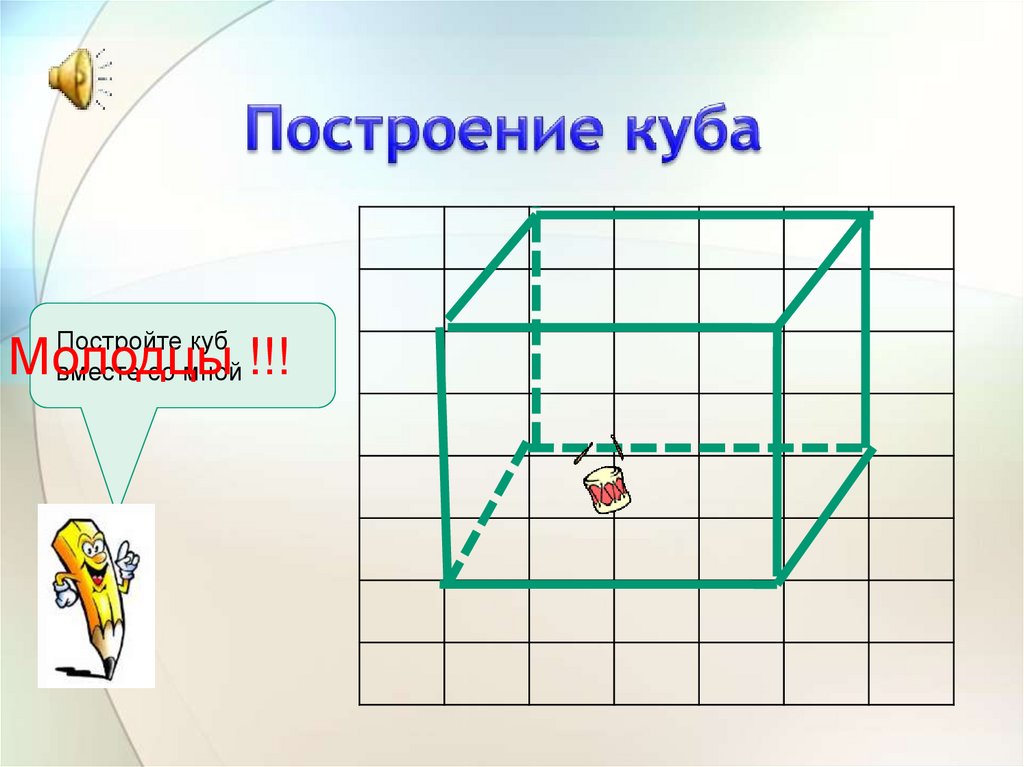 Обратите внимание на грань с жёлтым треугольником и
грань с зелёным треугольником. Очевидно, что эти грани будут смежными при
сборке кубика. При этом возможны четыре варианта взаимного расположения этих
граней при различных поворотах кубика.
Обратите внимание на грань с жёлтым треугольником и
грань с зелёным треугольником. Очевидно, что эти грани будут смежными при
сборке кубика. При этом возможны четыре варианта взаимного расположения этих
граней при различных поворотах кубика.
Теперь сравним с четырьмя предложенными вариантами. Сразу видим, что вариант первый неверный. Вариант второй неверный. Очевидно, что вариант третий тоже неверный. А вот вариант четвёртый верный, так как грани, на которых изображены треугольники, расположены верно. При этом на верхней грани должен быть изображён синий круг. Действительно так.
Таким образом, мы с вами выяснили, что из данной развёртки получится куб под номером 4.
Данную задачу вы можете решить ещё одним способом. А именно нарисовать данную развёртку на бумаге. Причём удобнее это сделать на листочке в клеточку, тогда вам не надо будет использовать линейку, чтобы соблюдать размеры кубика. Вы просто будете отсчитывать нужное количество клеточек.
Затем нужно будет раскрасить нарисованную развёртку и вырезать. Потом свернуть из неё куб и склеить его. После чего вы легко можете сравнить получившийся куб с каждым из предложенных вариантов и выбрать верный.
Задача вторая. Модель куба с длиной ребра 4 сантиметра окрасили в серую краску и распилили вдоль рёбер на кубики с длиной ребра 1 см. Сколько среди полученных кубиков: а) окрашенных с трёх сторон; б) окрашенных с двух сторон?
Решение.
Задача третья. На рисунке изображён каркас куба. Проведите видимые рёбра так, чтобы куб был «виден»: а) сверху слева; б) снизу справа.
Решение.
Задача четвёртая. На рисунке изображена фигура, сложенная из пяти кубиков. Какой вид будет иметь данная фигура, если смотреть на неё: а) спереди; б) слева; в) сверху?
Решение.
Методы построения геометрических тел в пространстве
Оглавление
Куб
Куб является самой первой и важной геометрической фигурой, с которой сталкивается любой, кто начинает учиться рисовать. Лучшей модели для развития объемно-пространственного мышления не существует. Рисунок куба формирует видение перспективы, является важнейшим источником знаний и умений рисования. В основе будущих проектных решений дизайнера почти всегда лежит куб или комбинация из кубов.
Лучшей модели для развития объемно-пространственного мышления не существует. Рисунок куба формирует видение перспективы, является важнейшим источником знаний и умений рисования. В основе будущих проектных решений дизайнера почти всегда лежит куб или комбинация из кубов.
Главное в рисунке куба — задать трехмерность, построить его основание с учетом перспективного сокращения и ракурса. А далее просто почти механически построить все грани, соблюдая пропорции и перспективную параллельность линий, сходящихся в точке на линии горизонта. Конечно, для того, чтобы все это выполнить, рисунок куба должен выглядеть конструкцией или, другими словами, прозрачным каркасом. Итак, рисуем каркас куба.
К сожалению, для некоторых начинающих куб является неким неинтересным, простым и бесполезным для рисования предметом. Позже часть таких «рисовальщиков» осознает объем собственной трагедии и будет затрачивать колоссальное количество энергии, чтобы заново научиться видеть законы перспективы. А другие так никогда и не увидят собственной слепоты. Потому что начинается все с рисунка обычного кубика.
Шестигранная призма
Шестигранная призма представляет собой геометрическое тело (с одной стороны, сечение этой формы выглядит как четырехугольник, а с другой стороны, это шестиугольник, причем вписывающийся в круг). Выполнить конструктивный рисунок этого геометрического примитива в пространстве очень сложно, если не увидеть в его конструктивной основе четырехгранную призму («кирпич» ), конструкция которой схожа с конструкцией куба и которую вы уже умеете рисовать.
Обратите внимание, что, выполняя рисунок этого геометрического примитива, мы уже стараемся понять его конструкцию как сумму более простых примитивов, таких как четырехгранная призма и две трехгранных призмы. Выражение «если не увидеть» очень точно отражает суть конструктивного рисунка.
Выполните каркасный рисунок «кирпича» (то есть четырехгранной призмы) в пространстве, соблюдая пропорциональные отношения высоты, ширины и глубины. На торцевых поверхностях «кирпича» проведите диагонали. В месте пересечения диагоналей мы получим две точки, которые будут находиться в центре торцевых поверхностей и через которые мы сможем построить перпендикулярное сечение. Оно будет проходить через фигуру четырехгранной призмы.
На торцевых поверхностях «кирпича» проведите диагонали. В месте пересечения диагоналей мы получим две точки, которые будут находиться в центре торцевых поверхностей и через которые мы сможем построить перпендикулярное сечение. Оно будет проходить через фигуру четырехгранной призмы.
Проведем отрезки из вершин четырехгранной призмы, практически повторяющие направление диагоналей, до пересечения с секущей плоскостью и получим еще четыре вершины шестигранной призмы. Соединим вершины между собою при помощи линий и получим конструктивный (каркасный) рисунок шестигранной призмы.
Если рисунок окажется не совсем верным, ищите причину в пропорциональных отношениях сторон четырехгранной призмы.
Шар
Шар является геометрическим примитивом. Он трехмерен, имеет все стороны трехмерного пространства, вписывается в куб. Вершины шара, вписанного в куб, находятся в центре поверхностей сторон куба (ил. 10).
Самый простой способ конструктивного построения шара выполняется так. Проведите две осевые линии, вертикальную и горизонтальную. От центра пересечения осевых линий — согласно пропорциональным отношениям шара с другими геометрическими предметами (если они есть) — отложите одинаковые отрезки на осевых линиях и постройте окружность.
Получится двухмерная поверхность в виде круга, но она не является шаром, потому что у нее отсутствует третье измерение, то есть глубина. Чтобы создать объем, надо горизонтальную осевую линию раскрыть до состояния квадратной плоскости в перспективе. Положение этой плоскости в пространстве будет зависеть от вашей точки зрения на этот предмет. Круг должен вписываться в квадрат: постройте окружность (сечение), которая будет в виде эллипса, через четыре точки. Таким образом, мы получили конструктивный рисунок шара в пространстве.
Можно развернуть и вертикальную осевую линию до состояния плоскости. Тогда конструктивный рисунок шара будет нас информировать не только о том, как мы воспринимаем геометрическую фигуру сверху или снизу, но и о том, как воспринимаем ее справа или слева. И, конечно, существует в этом еще один значительный плюс: мы получим две вершины шара. Одна вершина укажет на самую высокую точку шара в пространстве, а другая — на точку опоры, если шар находится на плоскости.
И, конечно, существует в этом еще один значительный плюс: мы получим две вершины шара. Одна вершина укажет на самую высокую точку шара в пространстве, а другая — на точку опоры, если шар находится на плоскости.
Цилиндр
Цилиндр также является геометрическим примитивом. Форма цилиндра образуется прямоугольным сечением, повернутым в пространстве на 360 градусов вокруг оси. Функцию оси выполняет одна из сторон этого прямоугольного сечения. Если рассмотреть формы сечения цилиндра (а их две), то одна из них представляет собой прямоугольник, а другая — круг.
Чтобы построить цилиндр у находящийся вертикально, надо провести вертикальную осевую линию, отложить на осевой пропорциональный отрезок, равный высоте цилиндра. Затем через крайние точки отрезка провести две горизонтальные осевые линии, строго перпендикулярные вертикальной. На горизонтальных осевых линиях отложите пропорциональные отрезки, равные ширине цилиндра, так, чтобы вертикальная осевая линия делила эти отрезки поровну. Соедините крайние точки горизонтальных отрезков между собой. Получите двухмерную прямоугольную фигуру с отношениями сторон, подобными сторонам цилиндра.
Создайте третье измерение. Постройте два эллипса (окружность в перспективе) через четыре точки. Верхний эллипс будет уже нижнего эллипса, так как находится в большем перспективном сокращении.
Основная проблема при построении цилиндра состоит не в создании эллипсов, а в их осевых линиях, потому что к их построению — по неопытности — серьезно не относятся. Нарушение в построении вертикальной осевой линии приводит к асимметрии и неустойчивости формы цилиндра. Нарушение же в построении горизонтальной осевой линии приводит к невозможности нарисовать правильный эллипс. А ведь все просто: вертикальная осевая линия рисунка соответствует вертикальной стороне листа рисунка, то же можно сказать и про горизонтальные осевые линии.
Особую сложность в конструктивном построении представляет форма цилиндра, лежащего на боковой поверхности. Круглое сечение цилиндра вписывается в квадрат (который относительно легко можно построить в пространстве) по четырем точкам. Значит, нам легче сначала построить в пространстве четырехгранную призму, соответствующую пропорциональным отношениям сторон цилиндра, а затем вписать в нее цилиндр.
Круглое сечение цилиндра вписывается в квадрат (который относительно легко можно построить в пространстве) по четырем точкам. Значит, нам легче сначала построить в пространстве четырехгранную призму, соответствующую пропорциональным отношениям сторон цилиндра, а затем вписать в нее цилиндр.
Как найти осевую линию, равную ширине цилиндра, в этом ракурсе? Построив в пространстве четырехгранную призму, найдите в ней срединную линию, проведите линию под прямым углом к срединной линии через центр боковой поверхности. На этой прямой находится отрезок, равный ширине цилиндра в этом ракурсе. Получается, что боковая поверхность цилиндра строится по шести точкам.
Почему мы так много говорим о построении цилиндра? Потому что вы с ним будете сталкиваться на каждом шагу, будет ли это предмет быта, драпировка, голова человека или фигура человека. Несмотря на все возрастающую сложность заданий по рисунку, вам придется абстрагировать сложные пластические формы до простых понятий, если вы, конечно, хотите их передать в рисунке.
Продолжаем тему конструктивного рисунка натюрморта из геометрических тел. Первое, что надо построить в рисунке натюрморта после создания композиции листа — это плоскость, на которой находятся предметы натюрморта. От того, как правильно вы нарисуете положение плоскости в пространстве, зависит успех всего рисунка. На плоскости создаются как бы следы предметов, и только после того, как вы убедитесь, что они действительно лежат на этой плоскости, приступайте к дальнейшему построению, то есть возводите каркас.
В большинстве натюрмортов некоторые геометрические предметы находятся на втором уровне. Это значит, что куб находится на плоскости стола, а на нем стоит конус. Пока вы не определите положение куба на плоскости стола, конус на кубе не построить. Типичной ошибкой является плоскость, опрокинутая на нас — предметы натюрморта, врезанные в плоскость стола (а на старших курсах — человеческие фигуры), будто скатываются с горки. Все дальнейшие построения предметов натюрморта выполняются с помощью методов, приведенных выше.
Конструктивное построение дает ясное понимание объема предметов натюрморта в пространстве и выполняется при помощи линий. Нарисованные предметы выглядят прозрачными каркасами.
Далее Работа над линиями
]]>
Как нарисовать куб в перспективе — Блог Sofia Art Academy
Поместите куб на плоскую поверхность.
Сядьте или встаньте (в зависимости от угла зрения, под которым вы хотите видеть свой рисунок), чтобы вы могли четко видеть три стороны куба.
Определите линию горизонта. Стоите вы или сидите, линия горизонта совпадает с уровнем ваших глаз. Проведите на листе линию, параллельную горизонту. Вытягивая карандашом руку, проверьте, где находится самый нижний угол куба относительно горизонта.
Чаще всего это нижний угол ближайшего к вам лица. Если вы решили нарисовать куб снизу (например, свесив с потолка), то это будет самый дальний угол, но в этом случае вам понадобится самый верхний угол. Поставьте точку на листе, предварительно прикинув пропорции будущего узора. Проведите вертикальную линию от отмеченной точки. Следует помнить, что все построения нужно выполнять очень слабо нажимая на карандаш, чтобы можно было легко стереть неправильные и вспомогательные линии.
Примеряем карандашом направление уходящих граней куба и переносим их на бумагу, доводя линию до пересечения с линией горизонта. Итак, мы получаем две точки схода. Теперь с помощью нашего незаменимого помощника измеряем высоту куба и отмечаем его на нашей вертикальной балке.
От полученной точки проводим прямые линии до точек схода. Измеряем ширину видимых сторон и проводим параллели нарисованному краю на рисунке.Помните, что все измерения следует проводить, вытягивая перед собой руку и держа карандаш строго горизонтально. Измерьте расстояния между вертикальными линиями сторон куба. На рисунке мы используем точные пропорции пропорций наших измерений. На лучах, идущих к линии горизонта, появились пересечения с дальними гранями куба. Если эти точки соединить со второй точкой схода, то все грани нашего куба найдут свои границы.Причем будут видны даже невидимые стороны. Это каркас будущего куба. Можно сразу стереть лишнее вокруг куба. Внутри пока оставим все как есть, чтобы лучше усвоить воздушную перспективу. Для этого возьмите мягкий карандаш и выделите на картинке ближайший к вам край.
На лучах, идущих к линии горизонта, появились пересечения с дальними гранями куба. Если эти точки соединить со второй точкой схода, то все грани нашего куба найдут свои границы.Причем будут видны даже невидимые стороны. Это каркас будущего куба. Можно сразу стереть лишнее вокруг куба. Внутри пока оставим все как есть, чтобы лучше усвоить воздушную перспективу. Для этого возьмите мягкий карандаш и выделите на картинке ближайший к вам край.
Теперь от него тянутся от темноты к свету по ребрам, отходя от себя. Возьмите ластик и сотрите самый дальний край, который не виден на этом кубе.Вымойте так, чтобы линии оставались слегка заметными. Теперь посмотрим на скелет. Он стал объемным. Хорошо изучив эту технику, приступаем к штриховке и штриховке. Принцип прост: чем ближе, тем ярче и контрастнее, тем дальше, тусклее и неразборчивее.
Как быстро и легко нарисовать куб (из воображения)
КАК НАРИСАТЬ КУБ (ПО ОСИ XYZ)
Расшифровка: Нарисуем кубы с осью xyz!
ось y z помогает визуализировать в 3-х измерениях.Вы будете рисовать кубики с любых точек обзора и с любых направлений, и мы собираемся получить эту ось x y z, чтобы помочь вам лучше визуализировать.
Итак, вы можете увидеть также некоторые -x, -y и -z, которые идут в противоположных направлениях. Но это всего лишь деталь, помните только x y z.
И прежде чем начать, я предлагаю вам загрузить Designer Starter Kit.
Это бесплатно.
ШАГ 1 | НАРИСОВАТЬ САМОЛЕТ
Что мы можем сделать с осью x y z вначале, так это начать рисовать плоскость земли, как… В общем, представьте:
- Если у вас есть товар, то это плоскость стола .
- Или, если у вас есть что-то в человеческом масштабе, например мотоцикл или автомобиль, самолет — это сама земля .

ШАГ 2 | ПОДНИМАТЬ КАЖДЫЙ УГОЛ
И тогда вам нужно приподнять каждый угол вертикальными линиями.
Убедитесь, что все вертикальные линии параллельны.
ШАГ 3 | Восстановите верхнюю поверхность куба
Используйте правила двухточечной перспективы, чтобы нарисовать верхнюю поверхность куба.
В случае, если этот шаг кажется вам слишком сложным, я предлагаю вам загрузить Designer Starter Kit, где вы получите все основы рисования в одно- и двухточечной перспективе, что будет действительно необходимо для этого урока. дня.
ШАГ 4 | Найдите ось XYZ в каждом углу
Итак, как вы можете видеть здесь, для каждого угла этого прямоугольника вы увидите некоторую мини-ось x y z. Поэтому я приглашаю вас всегда их визуализировать. И я люблю называть их «угол x-y-z».
ШАГ 5 | ПОДНИМИТЕСЬ «ПУТЬ ВНИЗ»
Давайте продолжим, не поднимая вверх, а «поднимая вниз».
Это помогает вам практиковать свое трехмерное зрение.
Итак, я предлагаю вам провести несколько тестов, сначала нарисовав одну плоскость коробки, а затем воссоздав ее всю. И вы видите оранжевым цветом главную ось x y z, которая помогла мне визуализировать мою точку зрения.
Итак, я предлагаю вам быстро нарисовать сбоку немного осей x, y, z.И вы можете потренироваться, чтобы попытаться согнуть их. Мол, ты получишь некоторую наклонность. И когда вы поймете, как это работает, вы должны будете тренироваться рисовать.
Это означает, что особо не беспокойтесь о том, насколько идеальными будут ваши линии. Просто быстрый рисунок, чтобы вы могли протестировать максимальное количество деталей в кратчайшие сроки, количество углов, просто экспериментируйте, хорошо.
Когда вы открываете для себя новое правило, новую технику, сначала вы пытаетесь понять все это шаг за шагом.И после того, как вам придется рисовать, чтобы экспериментировать, пытаясь применить это, чтобы вы запомнили это так же хорошо, как ваш мозг запомнил бы это, но также и мышцы вашей руки будут более автоматическими.
Так что не пытайтесь пока совершенствоваться.
Итак, с одной стороны справа мы начали с оси XYZ, а здесь, слева, мы начали с плоскости. Итак, это два разных подхода, которые вы можете получить.
Я приглашаю вас рисовать вместе со мной. Вы можете приостановить это видео в любое время.Перемотайте его назад. Сделайте его интерактивным и сосредоточьтесь на музыке. Что довольно расслабляет. Я стараюсь выбрать тот, который позволит вам чувствовать себя комфортно, когда вы рисуете.
Воспринимайте это как игру.
Ага, я нарисовал одну плоскость, потом другую, и я их соединил.
Возможность делать реплики под разными углами — это то, что поможет вам быстрее рисовать и начинать любую фигуру, потому что куб, коробка — это основа всего. Потому что именно отсюда вы сможете рисовать более сложные формы в будущем.
Итак, вот лишь краткий обзор основ, которые вы можете найти в Designer Starter Kit прямо здесь. Итак, мы используем вспомогательные линии перспективных линий, горизонтальную линию, точки схода и так далее.
Хорошо?
И это из того, что вам нужно сначала потренировать, а затем вы можете перейти на кубики выше. Хорошо?Итак, еще раз, если вы хотите получить все это поэтапно, ссылка есть в описании.
Вот будет версия с изгибом, вам просто нужно наклонить линию горизонта.
Итак, у нас есть куб, который тоже нужно наклонить.
Ну вот. x y, ось z здесь.
Ну вот.
Итак, мы будем учиться на повторении, как только вы овладеете техникой, повторяйте столько раз, сколько сможете. Не надо спешить. Нарисуйте их, чтобы быть безупречным. Будучи несовершенным, продолжайте. Делайте столько, сколько хотите.
Воспринимайте это как игру. Повеселись.
Выделите куб здесь полужирным шрифтом, чтобы он больше контрастировал с линиями построения.
Вот ось x y z.
Так что вы можете потренироваться, не стесняйтесь, присылайте мне по электронной почте (choutac@thedesignsketchbook. com) свои некоторые из своих набросков, если хотите показать мне. Мне очень любопытно посмотреть на ваши успехи, ребята.
com) свои некоторые из своих набросков, если хотите показать мне. Мне очень любопытно посмотреть на ваши успехи, ребята.
Здесь мы собираемся повторить все оси x y z, которые мы нарисовали из предыдущих кубов, с разных точек обзора и под разными углами. Хорошо?
Попробуйте нарисовать кубики разных размеров, некоторые из них будут больше других, некоторые будут более нарисованными, я бы сказал грубее, чем другие.
И если вы видите, на самом деле куб, который мне кажется лучше, — это тот, у кого самые грубые чувства. Потому что это дает больше жизни наброскам, вместо того, чтобы пытаться довести все до совершенства с помощью аккуратных линий. Чувствуете ли вы разницу между первым шагом и основной фазой, первой фазой наверху и средней?
Итак, x y, z в основном, но вы можете просто запомнить это как X как ширину, Y как высоту и Z как глубину. Хорошо? X — ширина, Y — высота, Z — глубина.
Здесь я выделил жирным шрифтом штриховку внизу, чтобы подчеркнуть, что это поле видно снизу. Хорошо?
Хорошо, давайте подведем итоги.
Давайте сменим ручку на что-нибудь посмелее.
Итак, первая фаза, что мы сделали? Начнем с того, что увидим в трех измерениях ось X Y Z, хорошо? Так что чем больше вы будете тренировать следующие этапы, тем более этот будет более интуитивным.
Итак, во-вторых, вы строите прямоугольник из этой оси x, y z. Хорошо?
Итак, сначала вы начнете с простых точек зрения.А в отношении трех: попробуйте разные углы, попробуйте разные углы, вы бросите вызов самому себе.
И вы можете начать с оси XYZ на A или второго метра B начать с плоскости. У вас есть два основных метода. Это не единственные два, но это два основных.
А потом я хотел бы предложить вам их нарисовать.
Последний, когда вы чувствуете, в любое время возвращайтесь к основам. Потому что научиться рисовать, научиться рисовать для продуктовых дизайнеров — это путешествие.Хорошо?
Итак, пройдите все эти пять шагов.
При необходимости вернитесь к основам в любой момент.
Есть только прогресс. И это то, что нам нравится.
Для дальнейшего изучения Как рисовать кубики ,
Я приглашаю вас попрактиковаться в испытании Cube Mania!
резьба — рисование куба в ggplot2
Введение
В этом посте рассказывается, как построить куб в ggplot2 используя -многопоточную библиотеку .
ggplot2 не включает понятие третьей пространственной оси, поэтому вместо этого после
манипулируя трехмерным объектом, мы используем перспективную проекцию, чтобы «сгладить» его грани и
вершины на 2d плоскость. Эти спроецированные грани / вершины и будут построены ggplot2.
Подготовить объект к нанесению на карту
- Создать объект (здесь используется стандартный куб 2x2x2)
- Определите, где находится камера и куда она смотрит
- Преобразование объекта в пространство камеры
- Перспектива преобразования данных
# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# В пакете `thread` есть несколько встроенных объектов в` threaded :: mesh4dobj`
# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~
obj <- thread :: mesh4dobj $ cube
# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# Определить матрицу просмотра камеры i.е. преобразование камеры в мир
# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~
camera_to_world <- thread :: look_at_matrix (eye = c (1.5, 1.75, 4), at = c (0, 0, 0))
# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# Трансформируем объект в пространство камеры и делаем перспективную проекцию
# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~
obj <- obj%>%
transform_by (invert_matrix (camera_to_world))%>%
перспектива_проекция () как. data.frame (obj)%>% knitr :: kable ()
data.frame (obj)%>% knitr :: kable () | 1 | 4 | 1 | -0,0945866 | -0,0706857 | 1,581399 | 1 | -0,1855445 | -0,1356142 | -0,9732328 | 0,1523493 | 0,1540033 | -0,9762544 | 0,0748818 | 0,0756647 | 1,630932 | 1 | 1,630932 | ИСТИНА | |
| 1 | 4 | 2 | -0.1077957 | 0,2603509 | 1.631559 | 3 | -0,2154400 | -0,3088482 | -0,9263900 | 0,1523493 | 0,1540033 | -0,9762544 | 0,0748818 | 0,0756647 | 1,630932 | 1 | 1,630932 | ИСТИНА | |
| 1 | 4 | 3 | 0,2693976 | 0,2400504 | 1.687219 | 4 | -0.4345424 | -0,3475777 | -0,8308806 | 0,1523493 | 0,1540033 | -0,9762544 | 0,0748818 | 0,0756647 | 1,630932 | 1 | 1,630932 | ИСТИНА | |
| 1 | 4 | 4 | 0,2325119 | -0,1270569 | 1. 623552 623552 | 2 | -0,3706042 | -0,1407513 | -0,9180640 | 0.1523493 | 0,1540033 | -0,9762544 | 0,0748818 | 0,0756647 | 1,630932 | 1 | 1,630932 | ИСТИНА | |
| 2 | 4 | 1 | -0,1077957 | 0,2603509 | 1.631559 | 3 | -0,2154400 | -0,3088482 | -0,9263900 | 0,0000000 | 0,9394660 | 0,3426420 | 0,0013440 | 0.2085811 | 1.773502 | 5 | 1.773502 | ЛОЖЬ | |
| 2 | 4 | 2 | -0,3483420 | 0,1 | 61.823482 | 7 | 0,1812743 | 0,2777220 | 0,9434035 | 0,0000000 | 0,9394660 | 0,3426420 | 0,0013440 | 0,2085811 | 1.773502 | 5 | 1.773502 | ЛОЖЬ | |
| 2 | 4 | 3 | 0.1921159 | 0,1435705 | 1.951750 | 8 | -0,6699657 | 0,4605475 | 0,5822731 | 0,0000000 | 0,9394660 | 0,3426420 | 0,0013440 | 0,2085811 | 1. 773502 773502 | 5 | 1.773502 | ЛОЖЬ | |
| 2 | 4 | 4 | 0,2693976 | 0,2400504 | 1.687219 | 4 | -0.4345424 | -0,3475777 | -0,8308806 | 0,0000000 | 0,9394660 | 0,3426420 | 0,0013440 | 0,2085811 | 1.773502 | 5 | 1.773502 | ЛОЖЬ | |
| 3 | 4 | 1 | 0,2325119 | -0,1270569 | 1.623552 | 2 | -0,3706042 | -0,1407513 | -0,9180640 | 0.9631644 | -0,1369155 | 0,2314485 | 0,2119637 | -0,0287422 | 1,767221 | 4 | 1,767221 | ЛОЖЬ | |
| 3 | 4 | 2 | 0,2693976 | 0,2400504 | 1.687219 | 4 | -0,4345424 | -0,3475777 | -0,8308806 | 0,9631644 | -0,1369155 | 0,2314485 | 0.2119637 | -0,0287422 | 1,767221 | 4 | 1,767221 | ЛОЖЬ | |
| 3 | 4 | 3 | 0,1921159 | 0,1435705 | 1. 951750 951750 | 8 | -0,6699657 | 0,4605475 | 0,5822731 | 0,9631644 | -0,1369155 | 0,2314485 | 0,2119637 | -0,0287422 | 1,767221 | 4 | 1.767221 | ЛОЖЬ | |
| 3 | 4 | 4 | 0,1538294 | -0,3715328 | 1,806364 | 6 | 0,3411191 | 0,1021382 | 0,9344547 | 0,9631644 | -0,1369155 | 0,2314485 | 0,2119637 | -0,0287422 | 1,767221 | 4 | 1,767221 | ЛОЖЬ | |
| 4 | 4 | 1 | -0.0945866 | -0,0706857 | 1,581399 | 1 | -0,1855445 | -0,1356142 | -0,9732328 | -0,6370835 | 0,0 | 5-0,7654561 | -0,2099435 | 0,0306140 | 1.689395 | 3 | 1.689395 | ИСТИНА | |
| 4 | 4 | 2 | -0,28 | -0,2575617 | 1.721140 | 5 | -0. 1542710 1542710 | -0,1026941 | -0,9826771 | -0,6370835 | 0,0 | 5-0,7654561 | -0,2099435 | 0,0306140 | 1.689395 | 3 | 1.689395 | ИСТИНА | |
| 4 | 4 | 3 | -0,3483420 | 0,1 | 61.823482 | 7 | 0,1812743 | 0,2777220 | 0,9434035 | -0.6370835 | 0,0 | 5-0,7654561 | -0,2099435 | 0,0306140 | 1.689395 | 3 | 1.689395 | ИСТИНА | |
| 4 | 4 | 4 | -0,1077957 | 0,2603509 | 1.631559 | 3 | -0,2154400 | -0,3088482 | -0,9263900 | -0,6370835 | 0,0 | 5-0,7654561 | -0.2099435 | 0,0306140 | 1.689395 | 3 | 1.689395 | ИСТИНА | |
| 5 | 4 | 1 | -0,0945866 | -0,0706857 | 1,581399 | 1 | -0,1855445 | -0,1356142 | -0,9732328 | 0,0000000 | -0,5988573 | -0,8008558 | 0,0006763 | -0,2067093 | 1. 683114 683114 | 2 | 1.683114 | ИСТИНА | |
| 5 | 4 | 2 | 0,2325119 | -0,1270569 | 1.623552 | 2 | -0,3706042 | -0,1407513 | -0,9180640 | 0,0000000 | -0,5988573 | -0,8008558 | 0,0006763 | -0,2067093 | 1.683114 | 2 | 1.683114 | ИСТИНА | |
| 5 | 4 | 3 | 0.1538294 | -0,3715328 | 1,806364 | 6 | 0,3411191 | 0,1021382 | 0,9344547 | 0,0000000 | -0,5988573 | -0,8008558 | 0,0006763 | -0,2067093 | 1.683114 | 2 | 1.683114 | ИСТИНА | |
| 5 | 4 | 4 | -0,28 | -0,2575617 | 1.721140 | 5 | -0.1542710 | -0,1026941 | -0,9826771 | 0,0000000 | -0,5988573 | -0,8008558 | 0,0006763 | -0,2067093 | 1.683114 | 2 | 1. 683114 683114 | ИСТИНА | |
| 6 | 4 | 1 | -0,28 | -0,2575617 | 1.721140 | 5 | -0,1542710 | -0,1026941 | -0,9826771 | -0.2439436 | -0,2465920 | 0,9379147 | -0,0728616 | -0,0737928 | 1,825684 | 6 | 1,825684 | ЛОЖЬ | |
| 6 | 4 | 2 | 0,1538294 | -0,3715328 | 1,806364 | 6 | 0,3411191 | 0,1021382 | 0,9344547 | -0,2439436 | -0,2465920 | 0,9379147 | -0.0728616 | -0,0737928 | 1,825684 | 6 | 1,825684 | ЛОЖЬ | |
| 6 | 4 | 3 | 0,1921159 | 0,1435705 | 1.951750 | 8 | -0,6699657 | 0,4605475 | 0,5822731 | -0,2439436 | -0,2465920 | 0,9379147 | -0,0728616 | -0,0737928 | 1,825684 | 6 | 1.825684 | ЛОЖЬ | |
| 6 | 4 | 4 | -0,3483420 | 0,1 | 6 1. 823482 823482 | 7 | 0,1812743 | 0,2777220 | 0,9434035 | -0,2439436 | -0,2465920 | 0,9379147 | -0,0728616 | -0,0737928 | 1,825684 | 6 | 1,825684 | ЛОЖЬ |
Постройте точки для вершин объекта
-
с резьбойопределяет укрепление.Функция mesh4d (). - Если объект
mesh4dзадан в качестве данных для вызоваggplot2,ggplot2будет автоматически использоватьfortify ()для преобразования в data.frame. - , т.е. поскольку
многопоточныйопределяетfortify.mesh4d (), мы можем вызватьggplot2напрямую с объектомmesh4d.
ggplot (obj, aes (x, y)) +
geom_point () +
theme_void () +
тема (legend.position = 'none') +
Coord_equal () Постройте контур каждого многоугольника
- Каждый элемент имеет уникальный
element_id, который используется как эстетика группы - Установите
fill = NA, color = 'black', чтобы рисовать только границы каждого многоугольника.
ggplot (obj, aes (x, y, group = element_id)) +
geom_polygon (fill = NA, color = 'black', size = 0,2) +
theme_void () +
тема (legend.position = 'none') +
Coord_equal () Точечный рендеринг скрытых линий
- Чтобы нарисовать скрытых элементов другим способом, используйте переменную
hidden. -
скрыто— это логическая переменная, указывающая, обращен ли треугольник или четырехугольник подальше от камеры.
- Здесь другой тип линии
ggplot (obj, aes (x, y, group = element_id)) +
geom_polygon (fill = NA, color = 'black', aes (linetype = hidden, size = hidden)) +
scale_linetype_manual (values = c ('TRUE' = "пунктирный", 'FALSE' = 'solid')) +
scale_size_manual (значения = c ('ИСТИНА' = 0,2, 'ЛОЖЬ' = 0,5)) +
theme_void () +
тема (legend.position = 'none') +
Coord_equal () Удаление скрытой линии
- Здесь тип линии
с нулевой ширинойиспользуется для скрытых элементов, чтобы скрыть их.
ggplot (obj, aes (x, y, group = element_id)) +
geom_polygon (fill = NA, color = 'black', aes (size = hidden)) +
scale_size_manual (значения = c ('ИСТИНА' = 0, 'ЛОЖЬ' = 0,5)) +
theme_void () +
тема (legend.position = 'none') +
Coord_equal () Простые закрашенные многоугольники
- При заливке многоугольников
ggplot2будет рисовать их в порядке переменнойgroup. - Если мы сгруппируем по
element_id, то полигоны будут нарисованы в том порядке, в котором они были определены.Это означает, что удаленные полигоны будут рисуйте поверх тех, которые действительно находятся близко к глазу. - Результат будет выглядеть странно — почти в стиле Эшера!
ggplot (obj, aes (x, y, group = element_id)) +
geom_polygon (fill = 'голубой', цвет = 'черный', размер = 0,2) +
theme_void () +
тема (legend.position = 'none') +
Coord_equal () Заполненные многоугольники — (1) Отбрасывайте скрытые элементы, чтобы они никогда не отображались
- Первый метод для рисования закрашенных многоугольников:
- сбросить скрытые элементы вручную
- Сделайте это путем явного преобразования объекта
mesh4dв данные. кадр, а затем фильтрация
чтобы сохранить только те элементы, которые не скрыты.
кадр, а затем фильтрация
чтобы сохранить только те элементы, которые не скрыты.
- Для
mesh4dобъектов, преобразованных в data.frames,скрытыйопределяется какTRUEдля любая грань, нормаль которой направлена к отрицательной оси Z (т.е. со смотровой площадки).
obj_df <- as.data.frame (obj)%>%
фильтр (! скрытый)
ggplot (obj_df, aes (x, y, group = element_id)) +
geom_polygon (fill = 'голубой', цвет = 'черный', размер = 0.2) +
theme_void () +
тема (legend.position = 'none') +
Coord_equal () Заполненные многоугольники — (2) Назначьте скрытым элементам заливку
NA , чтобы они отображались невидимо- Второй метод для рисования закрашенных многоугольников:
- невидимо рисовать скрытые элементы
- Сделайте это путем явного преобразования объекта
mesh4dв data.frame и затем вручную установите переменные, сопоставленные сзаливкойицветомна beNAдля скрытых элементов
obj_df <- as.data.frame (объект)%>%
мутировать (
оттенок = ifelse (скрытый, NA, 'голубой'),
linecolour = ifelse (скрытый, NA, 'черный')
)
ggplot (obj_df, aes (x, y, group = element_id)) +
geom_polygon (aes (fill = I (оттенок), color = I (linecolour)), size = 0,2) +
theme_void () +
тема (legend.position = 'none') +
Coord_equal () Залитые многоугольники — (3) Используйте переменную
zorder для управления порядком рисования- Третий метод для рисования закрашенных многоугольников:
- Нарисуйте элементы от самого дальнего до ближайшего
- Воспользуйтесь тем фактом, что элементы отображаются в порядке переменной
группы. - При преобразовании
mesh4dв data. frame переменная
frame переменная zorderсоздается, начиная с1для самого дальнего элемента, доnдля ближайшего элемента. - , т.е. изменить переменную
groupсelement_idнаzorder
ggplot (obj, aes (x, y, group = zorder)) +
geom_polygon (fill = 'голубой', цвет = 'черный', размер = 0,2) +
theme_void () +
тема (легенда.position = 'none') +
Coord_equal () Многоугольник с ложной заливкой
- Нормаль к каждой грани включена в представление data.frame как
fnx, fny, fnz - Путем вычисления скалярных произведений источника света, расположенного в сцене, дробная часть освещение можно было рассчитать для каждого элемента.
- Здесь затенение полностью имитируется с помощью суммы
fny + fnzдля затенения многоугольников.
ggplot (obj, aes (x, y, group = zorder)) +
geom_polygon (aes (fill = fny + fnz), color = 'black', size = 0.2) +
theme_void () +
тема (legend.position = 'none') +
Coord_equal () Как нарисовать куб
Возможно, это одна из самых простых форм для затенения, куб действительно предотвращает несколько проблем. Сегодня я помогу вам обнаружить некоторые ошибки, которые делают начинающие художники, пытаясь научиться рисовать.
Рисование куба
Поскольку куб имеет геометрическую форму, логично использовать систему перспективы для рисования куба.Я не хочу прямо сейчас превращать это в статью о рисовании перспективы только потому, что это станет слишком длинным обсуждением и ослабит фокус этой серии статей, а именно: как затенять формы, чтобы они выглядели реалистично и трехмерно. .
Если вы только приехали сюда и хотите узнать обо всех четырех основных формах, вы можете начать с начала этой серии и наверстать упущенное:
- Четыре основных формы
- Как нарисовать цилиндр
- Как нарисовать конус
- Как нарисовать сферу
Настройка куба
Самый простой метод рисования куба — это рисование с перспективой в одну точку. Я избавлю вас от всех тонкостей использования такого метода рисования. Скажем так, вы можете нарисовать трехмерный куб, просто соединив его передние углы с одной точкой.
Я избавлю вас от всех тонкостей использования такого метода рисования. Скажем так, вы можете нарисовать трехмерный куб, просто соединив его передние углы с одной точкой.
Как всегда, рисуйте контуры легко, потому что вы хотите, чтобы они исчезли к тому времени, когда вы закончите закрашивать куб. Контуры отвлекают от общей реалистичности нарисованного куба и служат только для того, чтобы направлять вас в начале рисования.
Как закрасить куб
Затенение куба резко отличается от других, более округлых форм, таких как цилиндр, конус и сфера, потому что куб полностью состоит из плоских сторон.В большинстве нормальных условий освещения это приводит к тому, что все его стороны отображаются как одно четное значение.
При закрашивании куба присвойте равное значение каждой стороне; не используйте градации значений.
Не знаю, почему, но как только молодые художники овладевают навыками затенения, многие из этих молодых художников становятся счастливыми с градиентом и хотят заштриховать все градациями значений. Это просто неверно с точки зрения реалистичности рисунка.Когда приходит время взглянуть на настоящий кубоподобный объект, вы можете более внимательно изучить его значения, а пока давайте сформулируем простое правило:
Если объект имеет плоскую сторону, эта сторона должна быть закрашена одним четным значением.
Вы заметите, что на чертеже куба каждой стороне присвоены разные значения. Это не должно вас удивлять, потому что на данный момент вы хорошо знаете, что свет по-разному отражается от разных частей объектов с разной интенсивностью, передавая им множество разных значений.
Сохраняйте простоту
Это было очень простое объяснение куба и его частей, но, честно говоря, это все, что вам нужно, чтобы начать рисовать реалистичные кубы. Вам просто нужно базовое понимание формы, и тогда ваши глаза помогут вам уловить все нюансы, когда вы начнете смотреть на настоящий куб под настоящим источником света.
Как насчет компонентов куба?
Если вы следили за предыдущими статьями о формах, то заметите, что я не упомянул о выделении, отраженном свете, основной тени или отбрасываемой тени.Причина в том, что нет особой пользы указывать на эти компоненты, поскольку отраженный свет и основная тень имеют тенденцию сбивать с толку в кубе, сбивать с толку, чем стоит обсуждать. Например, отраженный свет может иногда появляться с одной или нескольких сторон!
Даже отбрасываемая тень представляет некоторые трудности, если пытаться нарисовать ее с помощью воображения. Не беспокойтесь о отбрасываемой тени, когда тренируетесь. Когда придет время нарисовать настоящую кубическую форму, отбрасываемую тень будет легко увидеть, и у вас не будет проблем с определением ее формы!
Все, что вам нужно знать о кубе
- Используйте какую-нибудь перспективу, когда начинаете рисовать куб.
- Сосредоточьтесь на создании четких, равных значений для каждой стороны куба.
- В конце концов изучите реальную установку и используйте свои глаза, чтобы обнаружить форму отбрасываемой тени, значения каждой стороны куба и все другие детали, которые могут появиться.
Не забудьте…
Настоятельно рекомендуется использовать логику мышления в обучении рисованию. Это позволяет вам делать прогнозы относительно вашего предмета и дает подсказки относительно того, на что следует обращать внимание при обучении рисованию.Однако эта логика — только начало. Рано или поздно вам захочется изучить некоторые реальные объекты при реальном освещении и постараться нарисовать их реалистично.
Надеюсь, вы нашли новые идеи, когда учились рисовать, Я хотел бы, чтобы вы оставили мне комментарий ниже!
Ознакомьтесь с этими статьями по теме.
Как нарисовать куб углем
Это учебное пособие для моих студентов рисования и рисования в Колледже Олон.(Но не стесняйтесь использовать его, если хотите. )
)
Сфера — это основа для множества фигур, которые вам придется рисовать и раскрашивать. У меня есть PDF-файл, в котором вы можете скачать основные фигуры для распечатки и рисования здесь.
Я начинаю с угольного карандаша и держу его так, как Хамфри Богарт в тех старых фильмах держит свою сигарету.
Я начинаю с очень легкого наброска ромбовидной формы. Затем я беру сжатую угольную палочку и с ее стороны рисую вертикали.Я держу его в стиле «Богарта» и использую самый длинный край, почти как коньки, чтобы нарисовать вертикальные линии, спускающиеся с каждого угла.
То же самое используйте сжатую угольную палочку для создания диагональных линий. Сделайте все максимально легким! Вы хотите, чтобы линии исчезали, когда вы растушевываете плоскости.
Укажите на фоне таблицы.
Отбрасываемая тень представляет собой горизонтальную линию, которая начинается от того места, где углы встречаются со столешницей.Один из углов скрыт за корпусом куба. Форма отбрасываемой тени немного напоминает дом, поставленный боком.
А теперь момент истины! Я нарисовал все от руки, поэтому если я поставлю Т-образный квадрат на бумаге, будут ли мои вертикальные линии действительно вертикальными?
Неа! Они не вертикальные, так что мне нужно это исправить.
Теперь все лучше. Затем я беру кусок спрессованного угля и использую его как большую кисть для массирования самых больших теней и плоскостей.
Это прессованная угольная палочка. Это быстрый способ ввести значения, чтобы рисование происходило быстрее. Мой учитель Ирвин Гринберг говорил, что «большие художники используют большую кисть». Думаю, то же самое и с чертежными материалами.
Очень важно работать от фона к переднему плану.
Далее идет отбрасываемая тень.
Использование ластика для очистки краев, а также для растушевки и растушевки.
Нанесение тона на столешницу. Думаю, мне действительно следовало сделать это раньше.
Думаю, мне действительно следовало сделать это раньше.
Используя культю, растушуйте и выровняйте тона.
Используя угольный карандаш, сделайте небольшие штриховки и определите и измените значения.
Я считаю, что нанесение пометок — важная часть рисования. Я использую светлые линии, параллельные сторонам кубиков, чтобы выровнять тона и создать некоторую текстуру.
На данный момент этот рисунок является законченной версией, в которой используется маркировка.Важно продумать направление и частоту отметок. Некоторым художникам совсем не нравится нанесение меток, поэтому они полностью смешивают тона.
Далее я покажу вам, как это сделать ближе к концу. Здесь я использую ластик, чтобы начать делать это и исправить ситуацию. На данный момент я просто играю, чтобы все было по-другому.
Больше информации:http://www.kenney-mencher.com/
Дополнительные статьи и учебные пособия с практическими рекомендациями
Фигура человекаКак нарисовать портрет
Создание 3D-объектов с помощью WebGL — веб-API
Давайте рассмотрим нашу квадратную плоскость в трех измерениях, добавив еще пять граней, чтобы создать куб.Чтобы сделать это эффективно, мы собираемся переключиться с рисования с использованием вершин напрямую, вызвав метод gl.drawArrays () , чтобы использовать массив вершин в качестве таблицы и ссылаться на отдельные вершины в этой таблице, чтобы определить положение каждой из них. вершины грани, вызывая gl.drawElements () .
Учтите: каждая грань требует четырех вершин для ее определения, но каждая вершина является общей для трех граней. Мы можем передать намного меньше данных, построив массив из всех 24 вершин, а затем обращаясь к каждой вершине по ее индексу в этом массиве, вместо того, чтобы перемещать целые наборы координат.Если вам интересно, почему нам нужны 24 вершины, а не только 8, то это потому, что каждый угол принадлежит трем граням разного цвета, а одна вершина должна иметь один определенный цвет; поэтому мы создадим три копии каждой вершины трех разных цветов, по одной для каждой грани.
В этом примере библиотека glMatrix используется для математических вычислений с матрицами и вершинами. Вам нужно будет включить его, если вы создадите свой собственный проект на основе этого кода. Наш образец загружает копию из CDN в наш HTML-код .
Во-первых, давайте создадим буфер положения вершины куба, обновив код в initBuffers () . Это почти то же самое, что и для квадратной плоскости, но несколько длиннее, так как здесь 24 вершины (по 4 на каждую сторону):
постоянные позиции = [
-1,0, -1,0, 1,0,
1.0, -1.0, 1.0,
1.0, 1.0, 1.0,
-1.0, 1.0, 1.0,
-1,0, -1,0, -1,0,
-1,0, 1,0, -1,0,
1.0, 1.0, -1.0,
1.0, -1.0, -1.0,
-1,0, 1,0, -1,0,
-1.0, 1.0, 1.0,
1.0, 1.0, 1.0,
1.0, 1.0, -1.0,
-1,0, -1,0, -1,0,
1.0, -1.0, -1.0,
1.0, -1.0, 1.0,
-1,0, -1,0, 1,0,
1.0, -1.0, -1.0,
1.0, 1.0, -1.0,
1.0, 1.0, 1.0,
1.0, -1.0, 1.0,
-1,0, -1,0, -1,0,
-1,0, -1,0, 1,0,
-1.0, 1.0, 1.0,
-1,0, 1,0, -1,0,
];
Поскольку мы добавили z-компонент к нашим вершинам, нам нужно обновить numComponents нашего атрибута vertexPosition до 3.
{
const numComponents = 3;
...
gl.vertexAttribPointer (
programInfo.attribLocations.vertexPosition,
numComponents,
тип,
нормализовать,
шаг
компенсировать);
gl.enableVertexAttribArray (
programInfo.attribLocations.vertexPosition);
}
Нам также нужно построить массив цветов для каждой из 24 вершин. Этот код начинается с определения цвета для каждой грани, а затем использует цикл для сборки массива всех цветов для каждой из вершин.
const faceColors = [
[1.0, 1.0, 1.0, 1.0],
[1.0, 0.0, 0.0, 1.0],
[0,0, 1,0, 0,0, 1,0],
[0,0, 0,0, 1,0, 1,0],
[1.0, 1.0, 0.0, 1.0],
[1.0, 0.0, 1.0, 1.0],
];
var colors = [];
for (var j = 0; j После того, как массивы вершин сгенерированы, нам нужно построить массив элементов.
const indexBuffer = gl.createBuffer ();
gl.bindBuffer (gl.ELEMENT_ARRAY_BUFFER, indexBuffer);
const индексы = [
0, 1, 2, 0, 2, 3,
4, 5, 6, 4, 6, 7,
8, 9, 10, 8, 10, 11,
12, 13, 14, 12, 14, 15,
16, 17, 18, 16, 18, 19,
20, 21, 22, 20, 22, 23,
];
gl.bufferData (gl.ELEMENT_ARRAY_BUFFER,
новый Uint16Array (индексы), gl.STATIC_DRAW);
возвращаться {
позиция: positionBuffer,
цвет: colorBuffer,
индексы: indexBuffer,
};
}
Индексы Массив определяет каждую грань как пару треугольников, указывая вершины каждого треугольника в качестве индекса в массивах вершин куба. Таким образом, куб описывается как набор из 12 треугольников.
Затем нам нужно добавить код в нашу функцию drawScene () для рисования с использованием индексного буфера куба, добавив новые gl.bindBuffer () и gl.drawElements () звонков:
gl.bindBuffer (gl.ELEMENT_ARRAY_BUFFER, buffers.indices);
...
{
const vertexCount = 36;
константный тип = gl.UNSIGNED_SHORT;
const смещение = 0;
gl.drawElements (gl.TRIANGLES, vertexCount, тип, смещение);
}
Поскольку каждая грань нашего куба состоит из двух треугольников, на каждой стороне 6 вершин, или всего 36 вершин в кубе, хотя многие из них являются дубликатами.
Наконец, давайте заменим нашу переменную squareRotation на cubeRotation и добавим второй поворот вокруг оси x:
мат 4.повернуть (modelViewMatrix, modelViewMatrix, cubeRotation * . 7, [0, 1, 0]);
7, [0, 1, 0]);
Теперь у нас есть вращающийся анимированный куб, его шесть граней довольно ярко окрашены.
Посмотреть полный код | Открыть эту демонстрацию на новой странице
Жакор »3D Cube
Используя несколько быстрых шагов и несколько необычных движений мыши, вы можете создать трехмерный куб в Corel Draw. Давайте начнем!
ШАГ ОДИН
Выберите инструмент «Прямоугольник», удерживая нажатой клавишу Control, нарисуйте прямоугольник.Удерживая нажатой кнопку управления, прямоугольник останется пропорциональным.
ВТОРОЙ ШАГ
Теперь выберите инструмент «Указатель» и дважды щелкните свой прямоугольник. Вы должны увидеть следующее:
ШАГ ТРЕТИЙ
Как видите, есть 8 ручек на выбор. Возьмитесь за левую среднюю ручку и наклоните прямоугольник вверх. У вас должно получиться:
ШАГ ЧЕТВЕРТЫЙ
Теперь, когда у нас есть левая сторона, давайте создадим правую.Есть несколько способов сделать это, но мне нравится использовать несколько забавных движений мыши, чтобы дублировать и отражать форму. Вот как.
Используя инструмент выбора, щелкните фигуру, и вы должны увидеть следующее:
ШАГ ПЯТЫЙ
Как видите, есть 8 ручек на выбор. Возьмитесь за левую среднюю ручку и, удерживая нажатой клавишу Control, перетащите вправо, но не отпускайте. Вы должны увидеть дубликат, но чтобы фактически дублировать форму, вы должны щелкнуть правой кнопкой мыши.Сначала это немного сложно, но с практикой становится очень легко.
Итак, чтобы подвести итог, вы хотите взять левый средний маркер и, удерживая нажатой клавишу Control, перетащить вправо, но не отпускать. Удерживая нажатой клавишу Control и левую кнопку мыши, щелкните правой кнопкой мыши, чтобы дублировать форму. Вы должны увидеть следующее:
ШЕСТЬ ШАГ
Хорошо, теперь осталась только верхняя часть. Теперь мы могли бы создать еще один прямоугольник и попытаться уместить его, но это может занять некоторое время, чтобы попробовать поиграть с размером и добиться идеального соответствия.
 data.frame (obj)%>% knitr :: kable ()
data.frame (obj)%>% knitr :: kable () 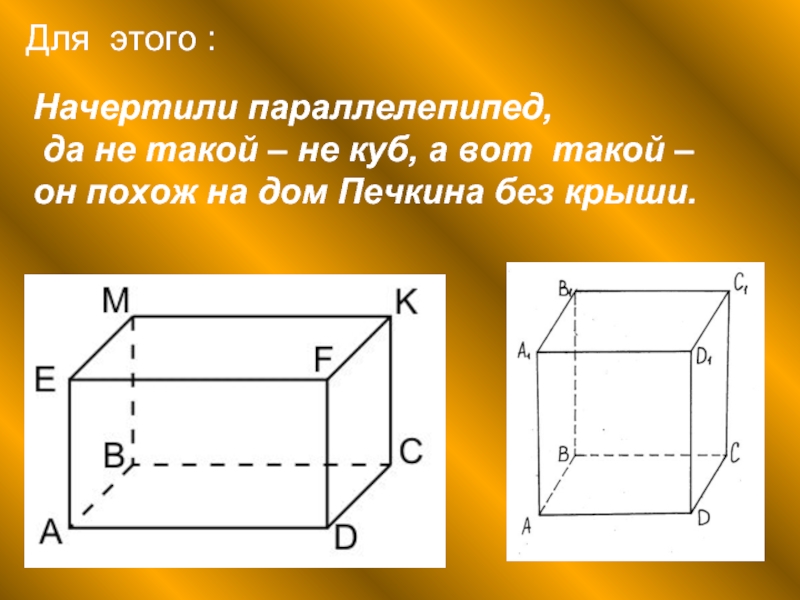
 кадр, а затем фильтрация
чтобы сохранить только те элементы, которые не скрыты.
кадр, а затем фильтрация
чтобы сохранить только те элементы, которые не скрыты. frame переменная
frame переменная  7, [0, 1, 0]);
7, [0, 1, 0]);