Как нарисовать звезду в квадрате: 7 способов нарисовать пятиконечную звезду

Как нарисовать звезду (и не только) в полярных координатах / Хабр

Вопрос о формуле для многоугольника в полярных координатах регулярно возникает на тематических ресурсах — и так же регулярно остаётся без внятного ответа. В лучшем случае попадается решение через функцию остатка от деления — что не является «чистым» с математической точки зрения, поскольку не позволяет производить над функцией аналитические преобразования. Видимо, настоящие математики слишком заняты решением проблем тысячелетия и поисками простого доказательства теоремы Ферма, чтобы обращать внимание на подобные банальные задачи. К счастью, в этом вопросе воображение важнее знания, и для решения этой задачи не нужно быть профессором топологических наук — достаточно знания школьного уровня.

Формула для равностороннего многоугольника в полярных координатах выглядит очень просто

и имеет следующие параметры:

— угол;
— количество выпуклых вершин;

— определяет, через какое количество вершин стороны будут лежать на одной прямой. Для него допустимы и отрицательные значения — от знака будет зависеть, в какую сторону будет выгибаться звезда;
— жёсткость — при мы получим окружность вне зависимости от прочих параметров, при — многоугольник с прямыми линиями, при промежуточных значениях от до — промежуточные фигуры между окружностью и многоугольником.

С этой формулой можно нарисовать звезду двумя путями:

1)

2) . В этом случае требуется сделать два оборота вместо одного:

Параметр влияет на многоугольник следующим образом (здесь он изменяется от -1 до 5):

Параметр в анимации:

Комплексная форма и модификации

Можно переписать исходную формулу в комплексном виде, и, несмотря на наличие в ней мнимых единиц, значение радиуса по-прежнему будет оставаться действительным:

На первый взгляд это может показаться бессмысленным, поскольку формула стала чуть более громоздкой — но не стоит спешить с выводами.

Во-первых, в ней отсутствует арксинус, что полностью меняет математический смысл формулы и позволяет по-другому посмотреть на построение звёздчатого многоугольника. Во-вторых, из неё также можно получить компактные формулы для частных случаев, например . В-третьих (и самое интересное), её можно творчески модифицировать и получать другие, неожиданные формы. Для того, чтобы появление возможной мнимой компоненты в радиусе не вызывало неоднозначности при вычислении, можно её сразу привести к декартовым координатам умножением на . Вот примеры некоторых модификаций:

Как вы наверняка заметили, вращение вектора перестало быть равномерным — и именно из-за появления мнимой составляющей в радиусе.

Квадрокруги и прочее

У нашей формулы есть замечательный частный случай — квадрат, формулу для которого можно выписать как

или

(выбирайте, какая больше нравится).

В чуть более развёрнутом случае можно определить промежуточные фигуры между кругом и квадратом через точку на плоскости

Можно также добавить вариативности этим фигурам с сохранением условия прохождения их через точку — модулируя непосредственно сам параметр в зависимости от угла таким образом, чтобы при прохождении через диагонали его множитель был равен единице. Например, подставив вместо функцию , мы получим дополнительный параметр , которым можно регулировать дополнительные изгибы. В частности, для получится следующее:

В ещё более развёрнутом случае можно определить не просто квадрат — а прямоугольник, и по прежнему в полярных координатах:

И даже посчитать его площадь (через эллиптические интегралы):

Примечание

Для крайних значений ( и ) эта функция имеет особые точки, которые можно посчитать через предел и они ожидаемо будут равны и .

Это позволит делать профили с переходом из окружности в прямоугольник с контролируемой площадью сечения. Здесь площадь константна:

А здесь площадь расширяется по экспоненциальному закону:

Переход к декартовым координатам

Любую формулу в полярных координатах можно выразить через уравнение в декартовых координатах, причём как минимум двумя способами — в зависимости от чего будет изменяться вид градиента на границе фигуры. Для этого достаточно посчитать угол через арктангенс от координат и привести формулу к константе через радиус-вектор вычитанием

или делением

Второй вариант предпочтительнее, поскольку даёт прямые градиенты вдоль сторон многоугольника.

Примечание

Здесь также нужно помнить, что в точке (0,0) возникает неопределенность из-за деления на ноль — которая, впрочем, легко разрешается через предел (который будет равным в первом случае и нулю во втором).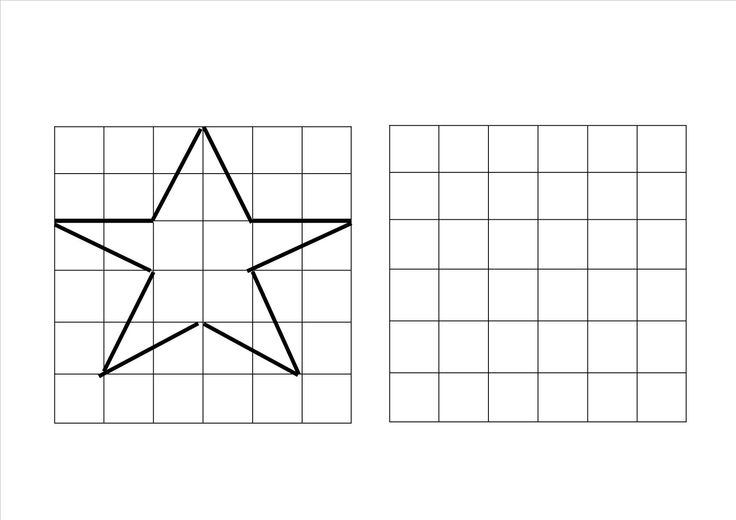

Выражение также можно упростить до , коэффициенты числителя которого при разложении образуют знакочередующий вариант последовательности A034839.

Значение формулы из правой части уравнения (во 2-м случае) будет меняться от до если точка попадает внутрь фигуры, и от до бесконечности — если нет. Выбирая различные функции для преобразования её в яркость, можно получать различные варианты растеризации. Для экспоненты ( для первого и для второго варианта) получим

или, если с насыщением

Можно использовать классический фильтр нижних частот , в котором — порядок фильтра, определяющий степень затухания.

Для первого варианта:

И для второго:

Можно использовать и кусочно-непрерывную функцию, явно задавая границы интерполяции.

Помимо растеризации как таковой, можно задавать и деформации — например, сжать шахматную доску в круг:

Или даже натянуть её на сферу:

Формула

Классический стиль повествования в математических текстах состоит из чередования лемм/теорем и их доказательств — как если бы доказуемые утверждения появлялись у авторов в голове откровением свыше. И хотя в этом и бывает доля истины, чаще появлению формул предшествует некоторая исследовательская работа, описание которой может дать большее понимание их смысла, чем формальное доказательство; а верность утверждений, в свою очередь, можно проследить через верность шагов, к ним приведших.

Так и здесь — если бы статья началась с формулы в комплексной форме, то её появление было бы неочевидным и контр-интуитивным, а заявленные свойства требовали бы дополнительных доказательств. Но в тригонометрической форме записи историю её появления вполне возможно проследить.

1) начинаем с самого простого случая — задаче начертить прямую в полярных координатах. Для этого нужно решить уравнение , решение которого очевидно .

2) далее аргумент секанса нужно «зациклить», чтобы обеспечить изломы в прямой. Именно на этом этапе другие решения используют «грязный хак» в виде остатка от деления. Здесь же используется последовательное взятие прямой и обратной функции синуса —

Такой подход позволяет производить стандартные математические операции над получившейся формулой,

например

можно её продифференцировать и получить функцию для прямоугольной волны:

Благодаря этой же записи можно упростить функцию квадрата в полярных координатах до более эстетического вида, используя представление тригонометрический функций в комплексном виде.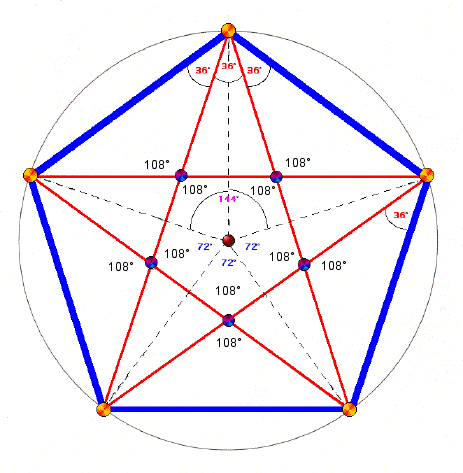

2))] /. \[Phi] -> ArcTan[x, y]
// TrigToExp // Simplify
// # /. {x -> Cos[\[Phi]], y -> Sin[\[Phi]]} &
// TrigToExp // Simplify // FullSimplify
↓

Заключение

Как видите, даже в такой простой и банальной вещи как многоугольник, можно найти и придумать что-то новое. И на этом история не заканчивается — осталась неизвестной формула площади для общего случая, осталась неизвестной формула для произвольного, а не только правильного многоугольника, остались без рассмотрения разложения в степенные и тригонометрические ряды. Также, вероятно, подобного рода формула существует и для 3-мерного случая.

Поэтому если вам говорят, что в математике уже всё придумано и остались лишь задачи недоступные пониманию обычного человека — не верьте. Есть много сугубо практических задач, о существовании которых настоящие математики не подозревают, или их решение им не интересно из-за отсутствия достаточного хайпа вокруг них, или потому что у них уже есть примерное представление путей достижения для их решения.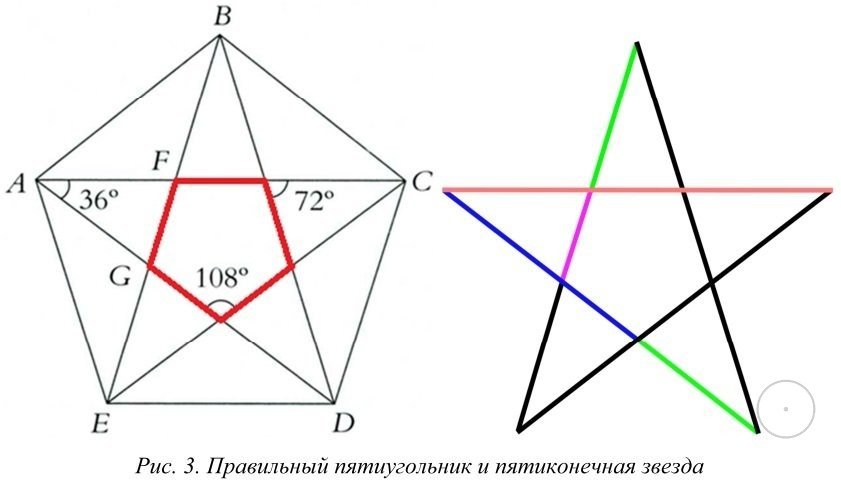

Не бойтесь браться за задачи, решение которых отсутствует в википедии, не бойтесь публиковать их решения и не бойтесь читать комментарии под статьями о бесполезности всего сущего.

P.S. скачать оригинальный документ для Mathematica можно здесь.

Пятиконечная звезда. Как правильно нарисовать ее быстро и просто

Пятиконечная звезда – наиболее почитаемый символ у всех народов мира во все времена. Ее изображения обнаружены у самых истоков цивилизации, когда еще не была изобретена письменность.

Самое первое изображение пятиконечной звезды, найденное археологами, датируется 3500 годом до нашей эры. Она была запечатлена на глиняной табличке, найденной при раскопках шумерского города Урук.

Символ звезды пользовался популярностью в Древнем Египте и Вавилоне. Его почитали древние римляне и греки, считая пятиконечную звезду символом круговорота в природе. Пять углов звезды греки ассоциировали с пятью элементами, из которых сотворен наш мир, – землей, водой, воздухом, огнем и эфиром.

Пятиконечная звезда является атрибутом гербов и флагов многих современных государств и присутствует на воинских знаках различия.

А вот нарисовать эту незамысловатую фигуру не так просто, как может показаться на первый взгляд.

Как нарисовать пятиконечную звезду, не отрывая карандаш от бумаги

Великий греческий мыслитель и математик Пифагор называл пятиконечную звезду математическим совершенством. Действительно, эту сложную фигуру можно нарисовать одной ломаной линией, не отрывая карандаша от листа бумаги и вернувшись в конце в ту же отправную точку, с которой был начат рисунок.

Темари — мастер-класс. Узнаем как научиться вышивать…

Мастер-класс, представленный в статье, показывает, как сделать японские шары темари из колготок,…

Вот такая она, сложная и простая на первый взгляд фигура – пятиконечная звезда. Как нарисовать ее одной ломаной линией, видно из рисунка.

Теперь узнаем, как нарисовать правильную пятиконечную звезду. Из измерительных приборов понадобятся линейка и транспортир.

Чтобы получилась звезда, нужно провести отрезки одинаковой длины таким образом, чтобы внутренние углы между всеми пятью вершинами фигуры были равны 36°. Практически это осуществляется следующим образом – чертится угол в 36°, от его вершины отмеряются отрезки одинаковой длины, и от их конечных точек проводятся новые прямые под углом 36°.

Можно также подойти к решению задачи немного иным способом, нарисовав равносторонний пятиугольник с вершинами углов в 106°, а затем соединив отрезками его противолежащие углы.

Если вы соблюдете все условия, у вас в конечном счете получится красивая пятиконечная звезда. Как нарисовать ее более простым способом, читайте далее.

Как нарисовать звезду с помощью циркуля и транспортира

Теперь вам понадобятся циркуль и транспортир. Так как в окружности 360°, то в 1/5 ее части – 72° (360 : 5 = 72). Приступаем к построению.

Узнаем как правильно нарисовать сердечко по клеточкам: три. ..

Как нарисовать сердечко по клеточкам? Рассмотрим три способа: простое симметричное, с крыльями и…

Начертите с помощью циркуля окружность. Отметьте на ней отправную точку – вершину звезды и середину окружности. Возьмите транспортир, совместите его центр с центром окружности, и по всей длине окружности отметьте рисками будущие точки вершин звезды через каждые 72°.

Останется соединить их прямыми, и получится красивая пятиконечная звезда. Как нарисовать ее, если под рукой не окажется транспортира? Без него можно обойтись, из инструментов понадобится лишь линейка и циркуль.

Как нарисовать звезду с помощью циркуля и линейки

Как нарисовать пятиконечную звезду циркулем? Рассмотрим вариант 1.

Чертим окружность. Измеряем ее диаметр с помощью линейки. Производим несложные математические действия: умножаем диаметр окружности на коэффициент 0,58779. Полученный результат – необходимая длина хорды (прямой, соединяющей 2 точки кривой линии, а в нашем случае – окружности), с помощью которой мы сможем разделить окружность на 5 равных частей.

Правильный пятиугольник: необходимый минимум информации

Толковый словарь Ожегова гласит, что пятиугольник представляет собой геометрическую фигуру,…

Например, диаметр окружности равен 7 см. Умножаем 7 х 0,58779 = 4,11453, округляем до десятых (так как нарисовать на бумаге отрезок более точной длины не представляется возможным), получим 4,1 см. Это и будет нужная длина хорды.

Осталось раздвинуть и зафиксировать ножки циркуля на данную величину, и можно делать насечки на окружности. Когда вы их соедините, получится пятиконечная звезда.

Как нарисовать фигуру другим способом? Рассмотрим вариант 2.

Для начала начертим правильный пятиугольник, вписанный в окружность. Как нарисовать правильную пятиконечную звезду на его основе, показано на рисунке 2.

Начертите циркулем окружность. Условно обозначим ее центр как О. Через точку О проведите прямую – диаметр нашей окружности. Прочертите радиус этой окружности таким образом, чтобы он был перпендикулярен диаметру. Точку пересечения радиуса с окружностью обозначим как V. Слева от точки О отложите расстояние, равное половине длины радиуса этой окружности, обозначьте его точкой А. Из точки А через точку V проведите полуокружность до пересечения с линией диаметра (на рисунке она выделена красным цветом) и обозначьте ее точкой В. Длина отрезка VB и будет длиной хорды, с помощью которой окружность разделится на 5 равных частей. Останется лишь соединить полученные точки в виде звезды.

Как нарисовать звезду | Пошаговое руководство

5,5 тыс. акций

Узнайте, как нарисовать великолепную звезду Star с помощью простых пошаговых инструкций и видеоуроков.

Следуя простым шагам, вы тоже легко нарисуете красивую звезду.

Перейти к пошаговым инструкциям.

Пятиконечная звезда использовалась в качестве символа во всем мире, охватывая тысячелетия человеческой цивилизации и пересекая культурные границы.

В самом общем смысле звезда представляет небеса, ночное небо и космическое пространство, где также можно увидеть кометы!

В средневековой Европе звезда использовалась для обозначения силы, власти и геральдики.

Прокрутите вниз, чтобы загрузить PDF-файл с этим руководством.

Пятиконечная звезда также используется различными религиями, включая ислам, веру Бахаи и религию Серрера в Западной Африке, а также многими военными подразделениями, нерелигиозными обществами, спортивными командами и организациями.

Хотите научиться рисовать идеально симметричную пятиконечную звезду?

Теперь вы можете это сделать, следуя этому простому пошаговому руководству по рисованию.

Чтобы нарисовать звезду, вам понадобится лист бумаги и письменные принадлежности, такие как ручка, карандаш или маркер.

Вы также можете использовать цветные карандаши, фломастеры или мелки, чтобы раскрасить готовый рисунок.

Также желательно иметь под рукой хороший ластик и прямую линейку.

Каждый шаг в этом руководстве по рисованию сопровождается иллюстрацией.

На каждой картинке новые строки, добавленные на этом шаге, выделены синим цветом; ранее нарисованные линии отображаются черным цветом.

Сначала вы, вероятно, захотите рисовать легко, так как по мере продвижения вы будете стирать некоторые исходные линии.

Если вам понравился этот урок, см. Также следующие руководства по рисованию: Крылья ангела, Огонь и Череп.

Пошаговые инструкции по рисованию звезды

Как нарисовать великолепную звезду для детей, начинающих и взрослых. Шаг 1

Для начала нарисуйте квадрат. Вы можете использовать линейку, чтобы обеспечить прямые линии и прямые углы.

Easy Star Drawing — Step 2

Проведите вертикальную линию посередине квадрата. Из этой же точки проведите линию с каждой стороны от первой. Эти линии будут встречаться с нижней частью квадрата между первой линией и сторонами квадрата.

Легкий рисунок звезды — шаг 3

Проведите прямую горизонтальную линию посередине квадрата. От каждого конца этой линии протяните прямую линию вниз и к центральной вертикальной линии. Эти линии будут встречаться с вертикальной линией на полпути между горизонтальной линией и нижней частью квадрата.

Easy Star Drawing — Шаг 4

От точки, где сходились предыдущие линии, проведите еще две линии. Эти линии будут встречаться с нижней частью квадрата в той же точке, что и почти вертикальные линии.

Простое рисование звезды. Шаг 5

От двух нижних точек звезды проведите две прямые линии, которые сойдутся в центре звезды.

Простое рисование звезды. Шаг 6

От двух боковых точек звезды проведите две прямые линии, которые сходятся в центре звезды.

Easy Star Drawing — Step 7

Проведите прямые линии от каждой точки внутреннего перевернутого пятиугольника к центру звезды.

Easy Star Drawing — шаг 8

Сотрите направляющие линии — как в звезде, так и в исходном квадрате.

Легкий рисунок звезды. Шаг 9

Раскрась свою звезду. Использование двух разных оттенков для чередующегося окрашивания звезды усилит трехмерный эффект звезды.

Другие замечательные уроки рисования Really Easy см. в посте 51 Easy and Fun Really Easy Drawing Ideas.

Простое, пошаговое руководство по рисованию звезды

Нажмите ЗДЕСЬ, чтобы сохранить урок в Pinterest!

Учебное пособие по рисованию звезды — легко и весело Страницы для печати

УСТРАНЕНИЕ НЕИСПРАВНОСТЕЙ ДЛЯ УЧАСТНИКОВ

Все еще видите рекламу или не можете загрузить PDF-файл?

Во-первых, убедитесь, что вы вошли в систему. Вы можете войти на странице входа в систему.

Если вы по-прежнему не можете загрузить PDF-файл, вероятное решение — перезагрузить страницу.

Это можно сделать, нажав кнопку перезагрузки браузера.

Это значок в виде круглой стрелки в верхней части окна браузера, обычно расположенный в верхней левой части (вы также можете использовать сочетания клавиш: Ctrl+R на ПК и Command+R на Mac).

Квадратные звезды

Квадратные звезды — это звездообразные параметрические фигуры с квадратными сторонами. Свойства квадратной формы звезды можно редактировать с помощью инструмента Node или панели Shape .

Квадратные звезды с разными свойствами: (A) квадратная звезда с шестью сторонами, (B) квадратная звезда с пятью сторонами, (C) квадратная звезда с загнутыми сторонами.

Рисование квадратных звезд

квадратных звезд можно нарисовать с помощью набора Square Star 9.0116 из набора инструментов приложения. Чтобы нарисовать квадратную звезду:

• Выберите инструмент Square Star из набора инструментов.
• Нажмите мышью на начальное место на холсте, это будет центр квадратной звезды.
• Перетащите мышь, чтобы задать радиус и вращение квадратной звезды.
• Удерживайте нажатой клавишу Shift , чтобы ограничить вращение квадратной звезды указанными пользователем приращениями (по умолчанию 45 градусов).
• Нажмите Вверх 9Клавиша со стрелкой 0116 для увеличения сторон квадратной звезды при перетаскивании.
• Нажмите клавишу со стрелкой вниз , чтобы уменьшить стороны квадратной звезды при перетаскивании.
• Отпустите кнопку мыши, чтобы создать квадратную звезду с выбранным радиусом и вращением.

Если представление документа повернуто, квадратная форма звезды будет нарисована с углом поворота, противоположным виду.

Параметры квадратной звезды по умолчанию можно установить, дважды щелкнув значок 9.0115 Квадратная звезда Значок инструмента на панели инструментов. Например: количество сторон квадратной звезды можно задать численно перед рисованием квадратных звезд.

Чтобы создать квадратную звезду, задав числовые свойства фигуры, щелкните точку на холсте. Откроется вид Square Star (описанный ниже), который содержит все свойства формы квадратной звезды. Установите необходимые значения и нажмите Ok , чтобы создать новый объект в форме квадратной звезды.

Редактирование квадратных звезд

Инструмент Node можно использовать для интерактивного редактирования квадратных звезд:

• Выберите объект в форме квадратной звезды.
• Выберите инструмент Node из набора инструментов приложения.
• Ручки показаны на каждой внутренней и внешней сторонах и в середине каждой стороны квадратной звезды.
• Отрегулируйте размер и радиус звезды, перетащив один из внешних боковых маркеров.
• Удерживайте Shift , чтобы ограничить вращение заданными пользователем приращениями.
• Удерживайте клавишу Control , чтобы изменить только радиус и сохранить фиксированный угол.
• Удерживайте клавишу Option (Mac) или Alt (Windows), чтобы изменить только угол и сохранить фиксированный радиус.
• Отрегулируйте изгиб сторон звезды, перетащив маркер в середине стороны звезды.
• Нажмите клавишу со стрелкой Вверх , чтобы увеличить стороны звезды.