Урок математики в 5-м классе по теме: «Куб»
Материалы к уроку.
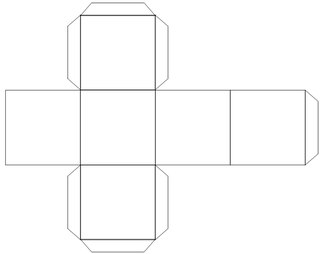
У каждого учащегося на парте лежит подготовленный заранее раздаточный материал (<Рисунок 1>, <Рисунок 2>, <Рисунок 3>, <Рисунок 4>) и склеенная модель куба.
Рис. 1
Рис. 2
Рис. 3
Рис. 4
Развертки куба №№ 2 и 3 (рис. 2 и 3) должны быть вырезаны, а развертка № 4 (рис. 4), являющаяся элементом домашнего задания, должна быть распечатана на цветной бумаге для принтеров, предпочтительно разных цветов.
Техническое оснащение урока: компьютер, проектор для демонстрации презентации, экран.
Цели урока:
- познакомить учащихся с понятием многогранника;
- дать учащимся понятие модели геометрического тела, получить представление о практическом применении геометрических знаний в реальной жизни;
- познакомить учащихся с изображением пространственных тел на плоскости;
- развивать пространственное воображение.

ХОД УРОКА
I. Организация начала урока
– Здравствуйте! Сегодня на уроке каждый из вас
получит подарок, который поможет не только
понять тему урока, но и поближе познакомит вас с
хорошо известным вам предметом (модель куба в
руках). Этот подарок лежит у вас на парте.
– Что это такое? (Куб)
– Молодцы! Сегодня на уроке нам понадобятся
простой карандаш, линейка, фломастеры, ластик,
раздаточный материал, который лежит на ваших
партах. Итак, НАЧИНАЕМ! Откройте, пожалуйста,
тетради, запишите число, классная работа и тему
сегодняшнего урока “КУБ”.
II. Сообщение темы, цели и задач урока
Слайд 1
– Сегодня на уроке мы поговорим о кубе. Узнаем,
как называются элементы куба, научимся чертить
куб, познакомимся с новыми понятиями, связанными
с кубом, узнаем, как находить площадь поверхности
куба, а также, где в жизни можно применить
полученные знания.
Запись на доске:
- элементы куба;
- построение куба;
- модель куба, развертка куба;
- площадь поверхности куба;
- применение полученных знаний.
– Где вы встречались с кубом в жизни?
Слайд 2
III. Актуализация знаний учащихся
Подготовка к активной учебно-познавательной деятельности на основном этапе урока.
– Что же такое куб? Невозможно найти человека, незнакомого с этим словом! “Кубики” – одна из первых детских игр. Кажется, что мы знаем о кубе все! Но так ли это? И сегодня мы это выясним.
IV. Усвоение новых знаний
– Возьмите в руки ваш куб. Посмотрите на него
внимательно. Из чего состоит поверхность куба? (Из
квадратов)
– Что вы знаете о квадрате? (У квадрата все
стороны равны!)
– А что можно сказать про квадраты, из которых
состоит поверхность куба? (Все квадраты равны)
– Правильно! Каждый такой квадрат называется
ГРАНЬЮ.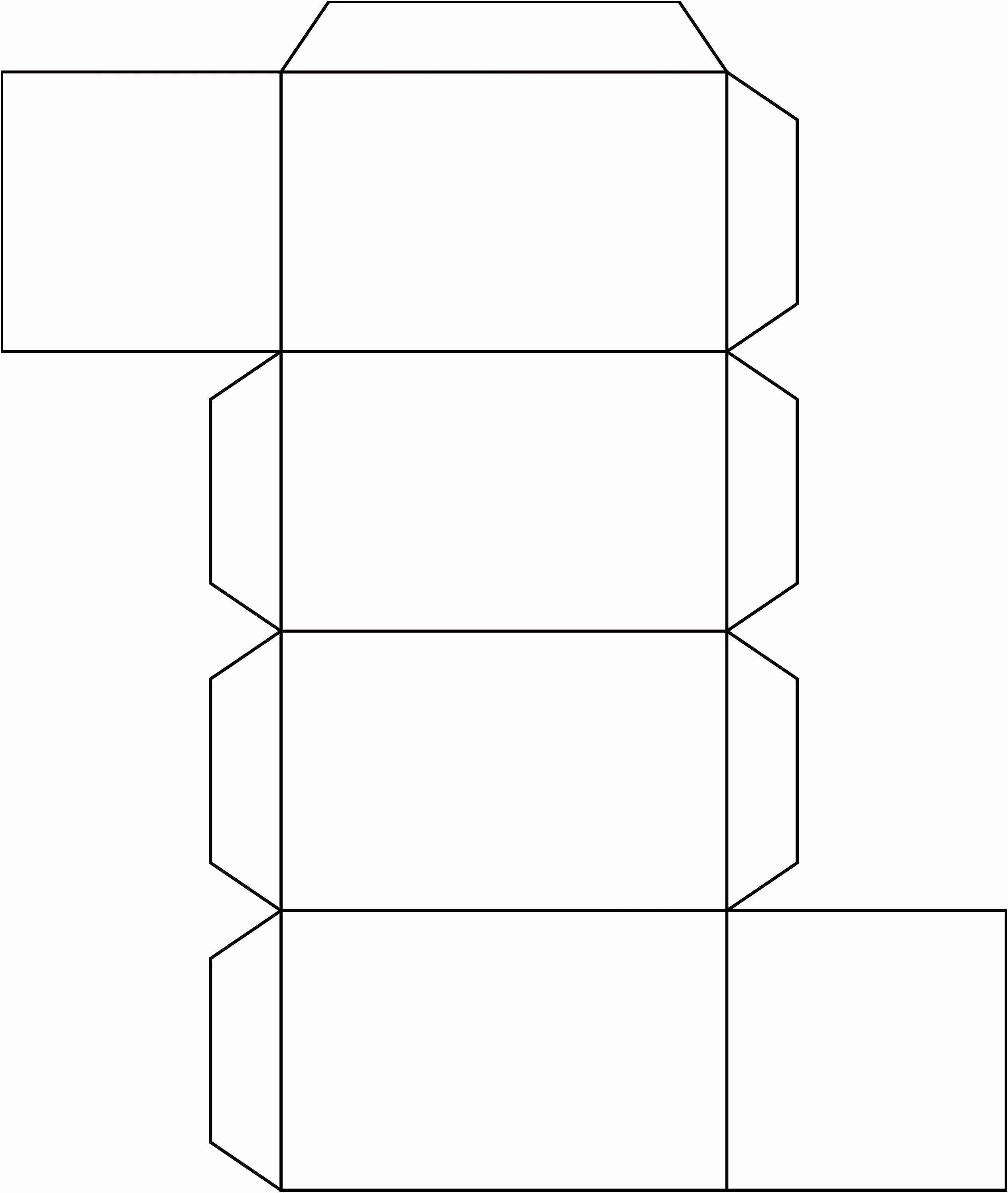 Новое понятие – ГРАНЬ. Именно поэтому куб
называется многогранником, т.е. он имеет много
граней. Поднимите куб и покажите мне его грань.
Новое понятие – ГРАНЬ. Именно поэтому куб
называется многогранником, т.е. он имеет много
граней. Поднимите куб и покажите мне его грань.
Слайд 3
– А сколько же граней у куба? Посчитайте и
ответьте! (Шесть)
– Правильно! Сторона грани называется РЕБРОМ
куба. РЕБРО – это тоже новое понятие. Покажите
мне ребро куба.
– Сколько ребер у куба? Не торопитесь ответить на
этот вопрос, сначала посчитайте! (Двенадцать)
– Правильно! Концы ребер называются ВЕРШИНАМИ
куба. ВЕРШИНА – еще одно новое понятие. Покажите,
пожалуйста, вершины куба.
– Сколько вершин у куба? (Восемь)
– Правильно! Итак, мы сейчас познакомились с
тремя новыми понятиями, связанными с кубом. Они
называются элементами куба. Какие элемента куба
вы знаете?
– Грань, ребро, вершина.
V. Первичное закрепление знаний
– А теперь, ответьте на вопросы:
- Сколько ребер сходится в одной вершине? (3)
- Сколько соседних граней имеет каждая грань? (4)
- Сколько ребер имеет одна грань? (4)
– Сейчас мы будем учиться чертить куб.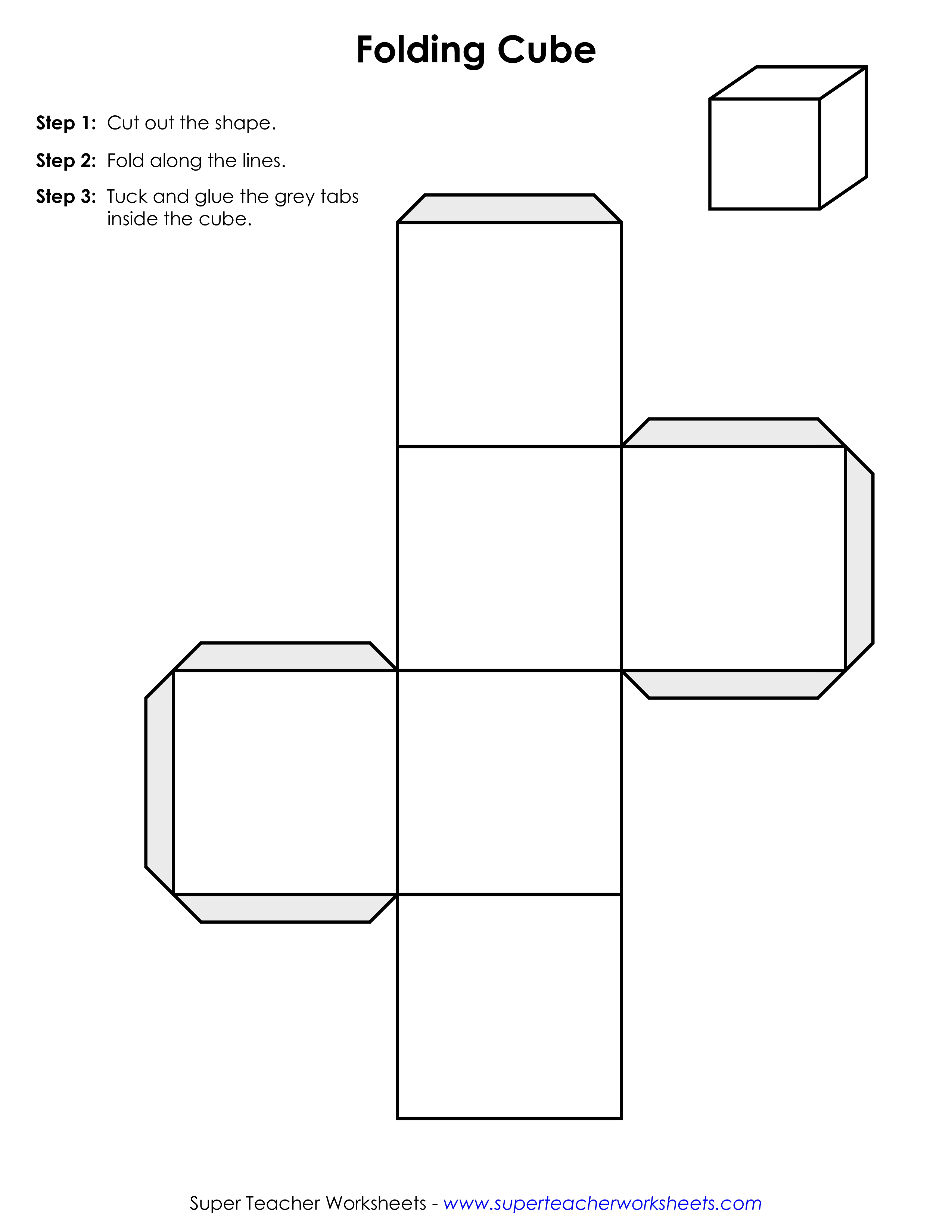 А это
нелегко! Ведь куб объемный, как же его можно
изобразить на плоском тетрадном листе? Надо
спланировать свою работу. ПЕРВЫЙ ШАГ: Строим
квадрат со стороной 2 см
А это
нелегко! Ведь куб объемный, как же его можно
изобразить на плоском тетрадном листе? Надо
спланировать свою работу. ПЕРВЫЙ ШАГ: Строим
квадрат со стороной 2 см
Слайд 4
– Похоже это на куб? (Нет)
– Чтобы изобразить куб на плоском листе,
потребуется волшебство! Для этого мы с вами
сейчас заглянем в будущее – в такой предмет как
черчение. Черчение нам поможет на плоском листе
начертить куб!
А теперь, внимание! Волшебником станет лишь тот,
кто будет внимательным и точно выполнит мои
указания! ВТОРОЙ ШАГ: Отметим три вершины
квадрата. ТРЕТИЙ ШАГ: от каждой отмеченной
вершины отступим 2 клетки вправо и 2 вверх и
отметим точки. ЧЕТВЕРТЫЙ ШАГ: Соединим
выделенные точки. А, теперь, похоже на куб? (Да!)
– Но есть одна неточность! Какая? Сколько граней
куба вы видите? (Три)
– А у куба сколько граней? (Шесть)
– Какие грани мы не видим, но знаем, что они есть? (Заднюю,
нижнюю, боковую левую)
– Но, поскольку мы с вами волшебники, то сейчас
построим невидимые ребра невидимых граней! ПЯТЫЙ
ШАГ: невидимые ребра обозначаются штрихом. Для
того чтобы построить невидимые ребра, отметим
невидимую вершину. От левой нижней вершины
отступим также 2 клетки вправо и 2 вверх и
поставим точку. Посмотрите, как надо соединить
эти точки. Отметьте и запишите в тетради элементы
куба.
Для
того чтобы построить невидимые ребра, отметим
невидимую вершину. От левой нижней вершины
отступим также 2 клетки вправо и 2 вверх и
поставим точку. Посмотрите, как надо соединить
эти точки. Отметьте и запишите в тетради элементы
куба.
Мы с вами научились на плоском листе бумаги
изображать объемное тело!
Слайд 5
Физминутка
– Мы немного устали, поэтому проведем физминутку. Встаньте, пожалуйста. (Выполняются упражнения с моделью куба в руках – разминка для глаз, для плечевого сустава, для позвоночника и т.п.).
VI. Закрепление знаний
– А теперь познакомимся с новыми понятиями, связанными с кубом! В этом нам помогут ребусы. Кто знает, что такое ребусы? Посмотрите, пожалуйста, на экран!
Слайд 6
– Попробуйте прочитать зашифрованное слово.
(МОДЕЛЬ)
– Правильно. Перевернутое изображение означает,
что слово читается не слева направо, как мы
привыкли, а наоборот, справа налево. Итак, что же
изображено? (Дом)
Перевернутое изображение означает,
что слово читается не слева направо, как мы
привыкли, а наоборот, справа налево. Итак, что же
изображено? (Дом)
– Правильно. “Перевернем” слово. Что
получилось? (Мод)
– А какое слово зашифровано во второй части
ребуса? (Ель)
– Итак, зашифровано слово МОДЕЛЬ. А какое слово
зашифровано во втором ребусе? (РАЗВЕРТКА)
– Правильно. Вторая часть ребуса – отвертка, но
перед рисунком стоят две запятые, показывающие,
что мы должны отбросить первые две буквы слова.
По правилам разгадывания ребусов единицу можно
прочесть как РАЗ. Итак, второе слово – РАЗВЕРТКА.
А что означает слово модель? Кто-нибудь знает? Где
вы встречались с этим словом? Незнакомое слово!
Воспользуемся словарем. Откроем
Энциклопедический словарь.
Слайд 7
– “Модель” – любой образ (мысленный или
условный: изображение, описание, схема, чертеж,
график, план, карта и т. п.) какого-либо объекта,
процесса или явления, используемый в качестве
его “заместителя”, “представителя” аналог,
изображение чего-либо.
п.) какого-либо объекта,
процесса или явления, используемый в качестве
его “заместителя”, “представителя” аналог,
изображение чего-либо.
Слайд 8
Кубы бывают разного размера, они могут быть
изготовлены из разных материалов, но они имеют
одинаковую форму – это и есть модель куба!
Кстати, запомните, пожалуйста, как пишется и
произносится слово “модель”. Какое еще одно
новое слово еще вы узнали из ребуса? (Развертка)
– От какого слова происходит слово “развертка”?
(Развернуть, раскрыть)
– Правильно! Посмотрите, пожалуйста, на экран. Мы
увидим, как куб “разворачивается”.
Слайды 9–16
– А сейчас возьмите развертку куба, изображенную на экране и “сложите” из нее куб. Сложили? Молодцы!!! Внимательно посмотрите на развертку и скажите, из каких фигур состоит развертка куба? Сколько таких фигур? (Из 6 квадратов)
– У каждого из вас на парте лежит лист (рис.
 1).
Возьмите его, пожалуйста.
1).
Возьмите его, пожалуйста.Слайд 17
– Можете ли вы, посмотрев на изображенные
фигуры, сказать, какие из них не являются
разверткой куба? Почему? (Фигуры № 1 и № 4 не
являются развертками куба)
– Почему? (Они состоят не из 6 квадратов)
– Возьмите фигуру № 5 и попробуйте изготовить
куб. Не получилось! Не всякая фигура, состоящая из
6 квадратов, является разверткой куба! Отложите
лист. А сейчас, мы определим, сколько бумаги
потребовалось, чтобы изготовить модель куба, с
разверткой которого мы уже работали. Т.е. узнать
площадь развертки. Что надо знать, чтобы найти
площадь развертки? (Площадь каждого квадрата)
– А чтобы узнать площадь квадрата, что нужно
знать? (Его сторону)
Измеряем и записываем прямо на развертке – 6 см.
– Чему равна площадь одного квадрата (грани)?
Решение можно записать на развертке. (36 см2)
(36 см2)
– Из скольких таких квадратов состоит развертка
куба? (Из 6)
– Как найти площадь всей развертки? (Площадь
одного квадрата (грани) умножить на 6)
– Сколько же квадратных сантиметров
потребовалось на развертку данного куба?
Запишите ответ на одной из граней и покажите мне.
Не забывайте писать наименования. (216 см2)
Слайд 18
VII. Обобщение и систематизация
– А сейчас – устная задача. Представим себе, что мы – дизайнеры! От детского сада поступил заказ на создание аквариума в форме куба с площадью грани – 1 м2. Посмотрите на экран.
Слайд 19
– Какое количество стекла нам надо заказать в
мастерской? Работаем устно! (5 м2)
– Правильно! Ведь рыбкам дышать нужно! У какой
грани нет противоположной? (У нижней)
VIII. Контроль и самопроверка знаний
Контроль и самопроверка знаний
– Молодцы! А сейчас, мы поиграем в игру “Найди грань!” Для этого снова возьмите листы раздаточного материала, лежащие на вашем столе – на них изображены развертки куба.
Слайд 20
– Три задания – развертка № 2 – самое простое задание, № 3 – более сложное, № 6 – самое сложное. Хорошо подумайте, прежде чем выбрать задание! А теперь, внимание! ЗАДАНИЕ! Посмотрите на экран и отметьте на каждой развертке нижнюю грань, так, как отмечено на экране. Ваша задача – мысленно сложить куб и обозначить верхнюю грань буквой “в”. Вам дается одна минута на выполнение задания. Не торопитесь, подумайте! Готовы? Давайте проверим. (Проверка на экране)
IX. Подведение итогов урока
- С каким многогранником мы сегодня работали? (С кубом)
- С какими элементами куба мы познакомились? (Грань, ребро, вершина)
- Я загадала элемент куба.
 Таких элементов у куба
8. Что это? (Вершина)
Таких элементов у куба
8. Что это? (Вершина) - Назовите элемент куба, который является четырехугольником. (Грань)
- Назовите элемент куба, который является отрезком. (Ребро)
- Почему куб называется многогранником? (Много граней)
- Какие новые слова вы узнали из ребусов? (Модель, развертка)
- Какое из этих понятий помогает изготовить куб? (Развертка)
- Как найти площадь развертки куба? (Площадь одного квадрата (грани) умножить на 6)
- А чему вы еще научились на уроке? (Чертить куб модель куба, его развертку)
– Где нам могут пригодиться эти знания? Я вам подскажу! Посмотрите на экран.
Слайд 21
– Скоро наступит праздник! Близится Новый год!
Я поздравляю вас с наступающим Новым годом! А вы
можете свой подарок упаковать в сундучок, сделав,
его в виде куба.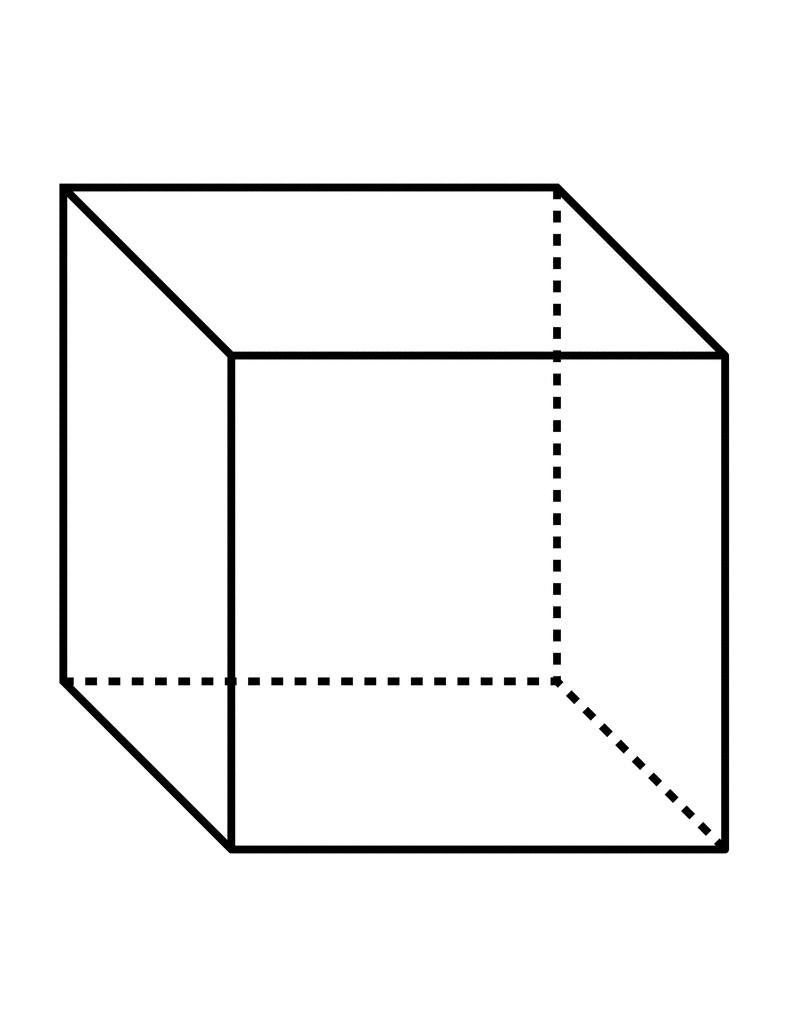 Также, вы можете сделать
новогоднюю игрушку на елку в виде куба (к одной из
вершин прикрепить нитку и украсить грани куба).
Также, вы можете сделать
новогоднюю игрушку на елку в виде куба (к одной из
вершин прикрепить нитку и украсить грани куба).
X. Информация о домашнем задании и инструктаж по его выполнению
– У каждого из вас на парте лежит развертка куба. Ваша задача дома изготовить куб из данной развертки (можно использовать другую развертку), не забудьте при вырезании оставить клапаны для склеивания, и на следующем уроке украсьте елку, которую вы можете сделать из цветного картона. А остальные кубы, вы можете перевязать ленточкой как подарок и положить под елку. И вы украсите свой класс к Новому году!
– Урок окончен! Всем спасибо! До свидания!
Приложение
УРОК 1. Рисуем линии.— Рисунок должен распологаться под прямым углом к центральному лучу зрения. — Нужно правильно держать в руке карандаш, он держится не так, как пишущий держит ручку.  — Проверяем подвижность правой руки на момент начала курса занятий. — Линия — язык рисунка. Рисуем линии. — Рисуем круг, определяем на глаз его центр, делим круг на четыре сектора и заполняем каждый сектор линиями до получения сплошного пятна. Для первого урока нам потребуется лист любой чистой бумаги, карандаш, можно фломастер или шариковая ручка. Желательно, сесть поближе к окну и чтобы свет падал слева. Освещение должно быть достаточным, чтобы не напрягать зрение, и в то же время нельзя, чтобы солнечные лучи падали на бумагу, отражаясь, свет будет ослеплять. Можно включить лёгкую музыку. Неопытные начинающие художники, обычно располагаются за столом, на котором горизонтально лежит бумага. Это не правильно, и я убедительно прошу, мой друг, никогда не работать в таком положении. Дело в том, что рисунок должен располагаться под прямым углом к центральному лучу зрения. Только при таком положении можно видеть рисунок правильно, без искажений. Я думаю, со временем у тебя будет мольберт, это специальный стол для рисования, позволяющий менять наклон рабочей плоскости. Нужно сразу научиться правильно, держать в руке карандаш, он держится не так, как пишущий держит ручку. Рисующий должен держать карандаш так, чтобы большой палец руки находился сверху, а снизу карандаш придерживался остальными пальцами, при этом мизинец, практически бездействует. Вначале это положение покажется тебе неудобным, но, освоившись, ты быстро оценишь все преимущества такого приёма. Это позволяет художнику держать руку вытянутой без всякого напряжения и проводить уверенные линии. Пальцы руки под карандашом слегка согнуты. Держится карандаш, в основном, большим, указательным и средним пальцами, остальные пальцы только слегка его придерживают. Карандаш должен находиться во время рисования под острым углом к бумаге, тогда он легко скользит по ней, оставляя лёгкую линию. В таком положении происходит самозатачивание стержня карандаша, и он всегда остаётся острым. А сейчас, мой друг, приготовились, прикрепили бумагу на плоскости, установленной примерно под 45 градусов. Сделаем в таком положении маленькую гимнастику для правой руки: повращаем вытянутую руку, вместе с карандашом вправо-влево, вправо-влево 10 – 15 раз. Передохнем и сделаем, столько же раз вращательные движения, теперь уже только кистью руки. Можно добавить упражнения для рук из своего любимого гимнастического комплекса. Такую гимнастику и для обеих рук, необходимо проводить перед каждым занятием рисования, пока твёрдость и подвижность рук не восстановятся до нужного для художника состояния. Проверим подвижность правой руки на момент начала нашего курса занятий. Для этого на прикреплённом листе бумаги определим на глаз, какого размера может уместиться окружность и где будет её нижняя точка. Попробуем нарисовать окружность, или то, что у нас получится, вращением руки, не отрываясь от бумаги, с левого нижнего положения, до правого, максимально нижнего положения намеченной окружности. Если начальная точка, полученной фигуры, похожей на окружность, слева внизу и конечная точка справа внизу, находятся на расстоянии двух сантиметров и менее, то есть – круг почти замкнулся, я поздравляю тебя, мой друг, подвижность руки хорошо сохранилась. Те, у кого результат получился хуже, не расстраивайтесь, занимаясь с нами, уже через 10 уроков, если вы проделаете это же упражнение и сравните его с сегодняшним рисунком, вы увидите свои успехи. Правильно будет начать занятия по рисунку с выполнения упражнения по рисованию линий. Линия это язык рисунка. Линии могут быть лёгкие, тонкие, изящные и весёлые или толстые, жёсткие, колючие. С их помощью можно передать различные настроения. Всё зависит от нажатия на карандаш (перо, кисть) и эмоционального состояния художника. Продолжим начатый рисунок и попробуем, полученную фигуру привести ближе к окружности. Не стирая нарисованной линии, будем рисовать линии рядом, пока не получим правильную окружность. На глаз определим центр нашей окружности и поставим точку. Для дальнейших занятий необходимо приобрести мольберт, специальную бумагу для рисования и обыкновенные простые карандаши различной мягкости, от В до 6В. Чаще всего будут использоваться карандаши средней мягкости. Резинкой для стирания, пока пользоваться не рекомендую. А ещё советую завести специальную папку для своих работ и сохранять в ней все рисунки, чтобы можно было видеть и самому оценить свои успехи. Не сомневайся, успехи будут, и будут соответствовать приложенным терпению и усилиям. Из этой папки, в конце учёбы, отберём работы на выставку, на которую пригласим своих друзей. |
три технологии на одной страничке
В основе самых сложных и необычные формы сооружений, устройств, механизмов лежат элементарные геометрические фигуры: куб, призма, пирамида, шар и другие. Для начала научитесь создавать самые простые фигуры, а после вы легко освоите более сложные формы.
Многие моделисты начинают свой путь с бумажных моделей. Это обусловлено доступностью материала (найти бумагу и картон не составляет трудности) и легкостью в его обработки (не требуются специальные инструменты).
Однако, бумага имеет и ряд характерных особенностей:
- капризный, хрупкий материал
- требует высокой аккуратности, внимательности, усидчивости при работе
По этим причинам бумага является материалом, как для начинающих, так и для настоящих мастеров и из нее создаются модели самой разной сложности.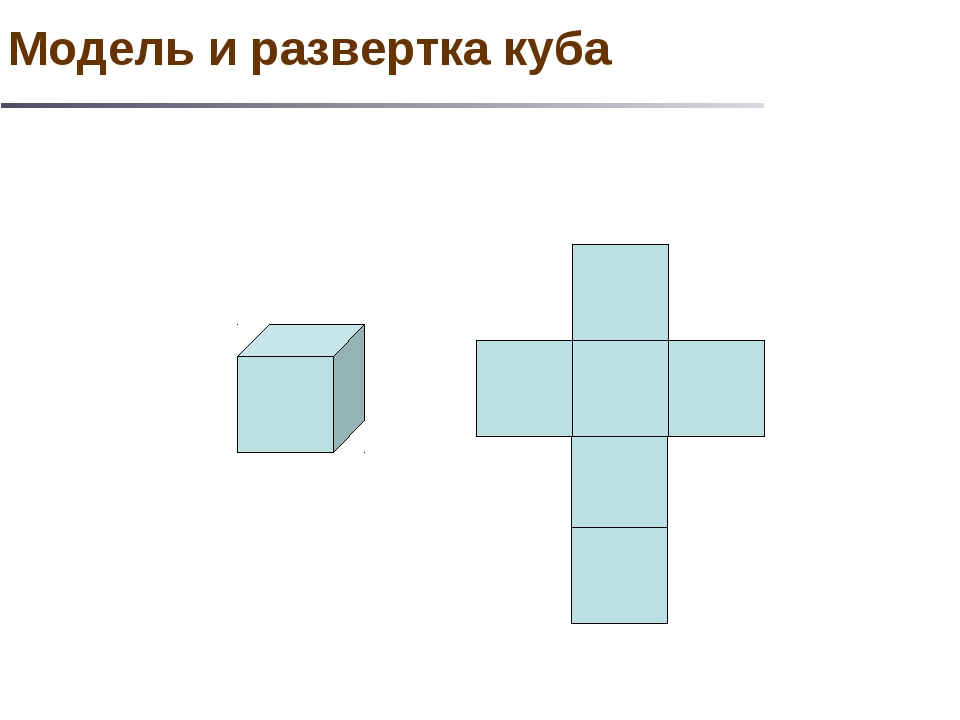
В этот статье мы изучим простейшие геометрические фигуры, которые можно сделать из бумаги.
Вам понадобятся следующие материалы:
- лист бумаги
- карандаш
- линейка
- ластик
- ножницы
- клей ПВА либо клеящий карандаш
- кисточка для клея, лучше из жесткой щетины
- циркуль (для некоторых фигур)
Как сделать куб из бумаги?
Куб – правильный многогранник, каждая грань которого представляет собой квадрат
Создание куба состоит из двух этапов: создание развертки и склеивание. фигуры. Для создания схемы вы можете воспользоваться принтером, просто распечатав готовую схему. Либо вы можете самостоятельно с помощью чертежных инструментов нарисовать развертку.
Рисование развертки:
- Выбираем размеры квадрата — одной стороны нашего куба. Лист бумаги должен быть шириной не менее 3 сторон этого квадрата и длиной немного более 4 сторон.
- Чертим в длину нашего листа четыре квадрата, которые станут боковыми сторонами куба.
 Рисуем их строго на одной линии, вплотную друг к другу.
Рисуем их строго на одной линии, вплотную друг к другу. - Над и под любыми из квадратов рисуем по одному такому же квадрату.
- Дорисовываем полоски для склеивания, с помощью которых грани будут соединяться между собой. Каждые две грани должны соединяться одной полоской.
- Куб готов!
После рисования развертка вырезается ножницами и склеивайте ПВА. Клей очень тонким слоем равномерно размазываем кистью по поверхности склеивания. Соединяем поверхности и закрепляем в нужном положении на некоторое время, с помощью скрепки или небольшого груза. Срок схватывания клея где-то 30-40 минут. Ускорить высыхание можно методом нагрева, например, на батарее. После склеиваем следующие грани, закрепляем в нужном положении. И так далее. Так постепенно вы проклеите все грани куба. Используйте небольшие порции клея!
Как сделать конус из бумаги?
Конус – тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.
Рисование развертки:
- Рисуем циркулем окружность
- Вырезаем сектор (часть круга, ограниченная дугой окружности и двумя радиусами, проведенными к концам этой дуги) из этой окружности. Чем больший сектор вы вырежете, тем острее будет конец конуса.
- Склеиваем боковую поверхность конуса.
- Измеряем диаметр основания конуса. С помощью циркуля рисуем окружность на листе бумаге требуемого диаметра. Дорисовываем треугольнички для склеивания основания с боковой поверхностью. Вырезаем.
- Приклеиваем основание к боковой поверхности.
- Конус готов!
Как сделать цилиндр из бумаги?
Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.
Рисование развертки:
- Рисуем прямоугольник на бумаги, в котором ширина — это высота цилиндра, а длина определит диаметр будущей фигуры. Отношение длины прямоугольника к диаметру определяется выражением: L=πD, где L- длина прямоугольника, а D — диаметр будущего цилиндра.
 Подставив в формулу требуемый диаметр, найдем длину прямоугольника, который будем рисовать на бумаге. Дорисовываем небольшие дополнительные треугольнички, которые необходимы для склеивания деталей.
Подставив в формулу требуемый диаметр, найдем длину прямоугольника, который будем рисовать на бумаге. Дорисовываем небольшие дополнительные треугольнички, которые необходимы для склеивания деталей. - Рисуем на бумаге два круга, диаметром цилиндра. Это будет верхнее и нижнее основания цилиндра.
- Вырезаем все детали будущего бумажного цилиндра.
- Склеиваем боковую поверхность цилиндра из прямоугольника. Даем детали высохнуть. Приклеиваем нижнее основание. Ждем высыхания. Приклеиваем верхнее основание.
- Цилиндр готов!
Как сделать параллелепипед из бумаги?
Параллелепипед – многогранник, у которого шесть граней и каждая из них параллелограмм.
Рисование развертки:
- Выбираем размеры параллелепипеда и величины углов.
- Чертим параллелограмм — основание. С каждой стороне дорисовываем боковые стороны — параллелограммы. От любой из боковой стороны дорисовываем второе основание. Добавляем полоски для склеивания. Параллелепипед может быть прямоугольным, если стороны прямоугольники.
 Если параллелепипед не прямоугольный, то создать развертку немного сложнее. Для каждого параллелограмма нужно выдержать требуемые углы.
Если параллелепипед не прямоугольный, то создать развертку немного сложнее. Для каждого параллелограмма нужно выдержать требуемые углы. - Вырезаем развертку и склеиваем.
- Параллелепипед готов!
Как сделать пирамиду из бумаги?
Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину.
Рисование развертки:
- Выбираем размеры пирамиды и количество ее граней.
- Рисуем основание — многогранник. В зависимости от количества граней это может быть треугольник, квадрат, пятиугольник или другой многогранник.
- От одной из сторон основания рисуем треугольник, который будет боковой стороной. Следующий треугольник рисуем так, чтобы одна сторона у него с предыдущим была общая и так далее. Так рисуем столько треугольников, сколько сторон в пирамиде. Дорисовываем полоски для склеивания в нужных местах.
- Вырезаем и склеиваем фигуру.
- Пирамида готова!
Большой выбор развёрток простых геометрических фигур.
Первое знакомство детей с бумажным моделированием всегда начинается с простых геометрических фигур, таких как кубик и пирамида. Не у многих получается склеить кубик с первого раза, иногда требуется несколько дней, чтобы сделать поистине ровный и безупречный куб. Более сложные фигуры цилиндр и конус требуют в несколько раз больше усилий нежели простой кубик. Если вы не умеете аккуратно клеить геометрические фигуры, значит и за сложные модели вам ещё рано браться. Займитесь сами и научите своих детей клеть эти «азы» моделирования по готовым развёрткам.
Для начала я, конечно же, предлагаю научиться клеить обычный кубик. Развёртки сделаны для двух кубиков, большого и маленького. Более сложной фигурой является маленький кубик потому, как клеить его сложнее, чем большой.
Итак, начнём! Скачайте развёртки всех фигур на пяти листах и распечатайте на плотной бумаге. Перед тем, как печатать и клеить геометрические фигуры обязательно ознакомьтесь со статьёй о том, как выбрать бумагу и как вообще правильно вырезать, сгибать и клеить бумагу.
Для более качественной печати советую использовать программу AutoCAD, и даю вам развёртки для этой программы , а также читайте, как распечатывать из автокада . Вырежьте развёртки кубиков с первого листа, по линиям сгиба обязательно проведите иголкой циркуля под железную линейку, чтобы бумага хорошо сгибалась. Теперь можно начинать клеить кубики.
Для экономии бумаги и на всякий пожарный я сделал несколько развёрток маленького кубика, мало ли вам захочется склеить не один кубик или что-то не получится с первого раза. Ещё одна несложная фигура это пирамида, её развёртки найдёте на втором листе. Подобные пирамиды стоили древние египтяне, правда не из бумаги и не таких маленьких размеров:)
А это тоже пирамида, только в отличие от предыдущей у неё не четыре, а три грани.
Развёртки трёхгранной пирамиды на первом листе для печати.
И ещё одна забавная пирамидка из пяти граней, её развёртки на 4-ом листе в виде звёздочки в двух экземплярах.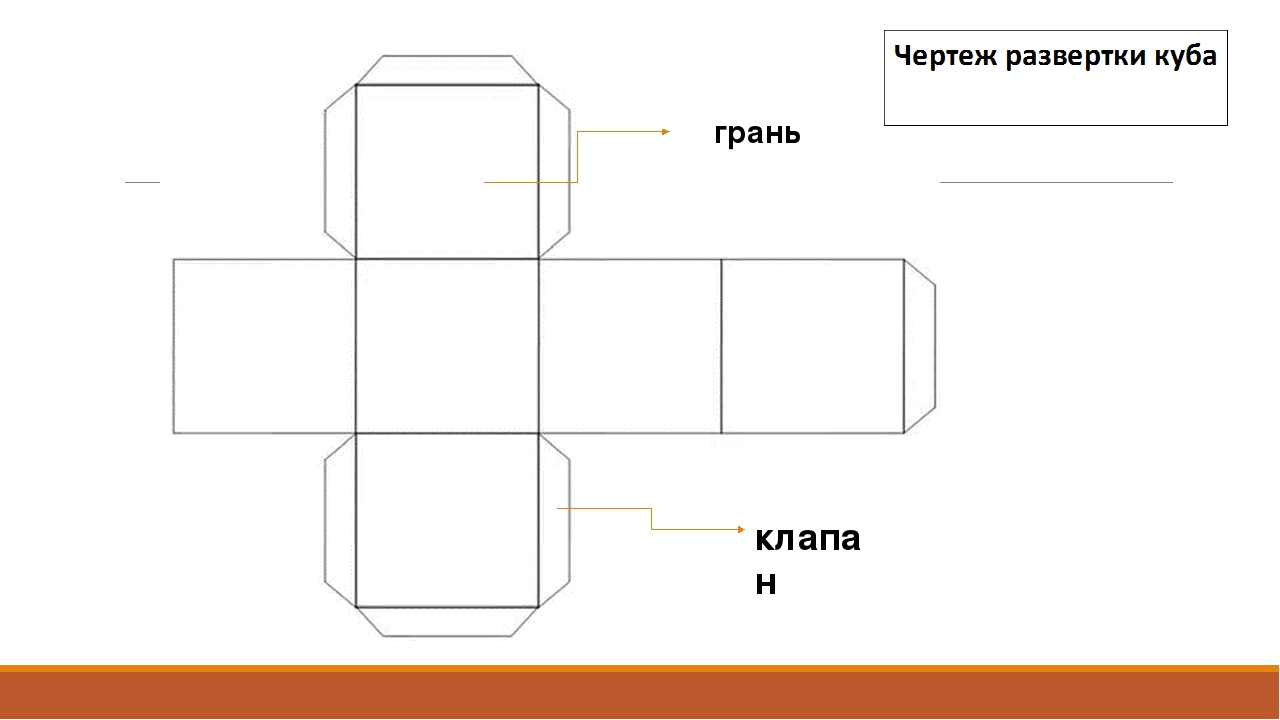
Более сложная фигура это пятигранник, хотя пятигранник сложнее начертить, нежели склеить.
Развёртки пятигранника на втором листе.
Вот мы и добрались до сложных фигур. Теперь придётся поднапрячься, склеить такие фигуры нелегко! Для начала обычный цилиндр, его развёртки на втором листе.
А это более сложная фигура по сравнению с цилиндром, т.к. в её основании не круг, а овал.
Развёртки этой фигуры на втором листе, для овального основания сделано две запасных детали.
Чтобы аккуратно собрать цилиндр его детали нужно клеить встык. С одной стороны дно можно приклеить без проблем, просто поставьте на стол заранее склеенную трубку, положите на дно кружок и залейте клеем изнутри. Следите, чтобы диаметр трубы и круглого дна плотно подходили друг к другу, без щелей, иначе клей протечёт и всё приклеится к столу. Второй кружок приклеить будет сложнее, поэтому приклейте внутри вспомогательные прямоугольники на расстоянии толщины бумаги от края трубы.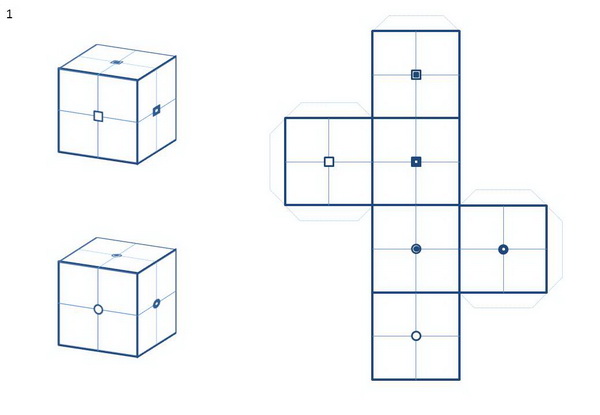 Эти прямоугольники не дадут упасть основанию внутрь, теперь вы без проблем приклеете кружок сверху.
Эти прямоугольники не дадут упасть основанию внутрь, теперь вы без проблем приклеете кружок сверху.
Цилиндр с овальным основанием можно клеить также как и обычный цилиндр, но он имеет меньшую высоту, поэтому тут проще вставить внутрь гармошку из бумаги, а наверх положить второе основание и по краю приклеить клеем.
Теперь очень сложная фигура — конус. Его детали на третьем листе, запасной кружок для днища на 4-ом листе. Вся сложность склеивания конуса в его острой вершине, а потом ещё будет очень сложно приклеить дно.
Сложная и одновременно простая фигура это шар. Шар состоит из 12-ти пятигранников, развёртки шара на 4-ом листе. Сначала клеится две половинки шара, а потом обе склеиваются вместе.
Довольно интересная фигура — ромб, её детали на третьем листе.
А теперь две очень похожие, но совершенно разные фигуры, их отличие только в основании.
Когда склеите эти обе фигуры, то не сразу поймёте, что это вообще такое, они получились какие-то совсем невосприимчивые.
Ещё одна интересная фигурка это тор, только он у нас очень упрощён, его детали на 5-ом листе.
И наконец, последняя фигура из равносторонних треугольников, даже не знаю, как это назвать, но фигура похожа на звезду. Развёртки этой фигуры на пятом листе.
На сегодня это всё! Я желаю вам успехов в этой нелёгкой работе!
Играя с ребенком различными геометрическими фигурками, вы помогаете ему развивать пространственное мышление и воображение. Он начинает понимать, что значит квадратный, круглый, кубический, шарообразный, прямоугольный и без труда сможет представить это в своей голове. Даже ученикам в школе на уроке геометрии преподаватели всегда показывают макеты различных фигур, что способствует лучшему усвоению геометрических теорем и аксиом. И, пожалуй, самое сложное и трудновыговариваемое слово для ребенка – «параллелепипед». Для того, чтобы освоить эту фигуру и понять её закономерности, предлагаем вам и вашему ребенку сделать параллелепипед из бумаги своими руками.
Для этого вам потребуется:
- плотная бумага (но не картон, иначе ребенку такая поделка доставит много трудностей), можно использовать лист из альбома;
- карандаш;
- линейка;
- ножницы;
- клей ПВА.
Чтобы понять, как делать параллелепипед из бумаги, необходимо вспомнить, как он выглядит и что из себя представляет. Эта фигура имеет 6 граней, каждая из которых является прямоугольником. Следовательно, развертка будет состоять из 6 соединенных между собой прямоугольников, находящихся в одной плоскости.
1. Как и любая объемная фигура, параллелепипед имеет длину, ширину и высоту. Именно от их значения будет зависеть размер полученной подделки. Определим желаемые величины и запишем их.
2. Приступим к начертанию схемы прямоугольного параллелепипеда на бумаге. Помните, что бумага не должна быть слишком тонкой, она легко намокнет от клея и покоробится, тогда фигурка не получится ровной, а излишне толстый картон будет плохо сгибаться и трескаться на изгибах.
3. Начертим горизонтальную линию, длина которой будет равна сумме ширины и высоты, умноженных на два. Затем из каждого конца линии опустим перпендикуляр, равный длине предполагаемого параллелограмма. Между ними проведем линию, параллельную первой.
4. Теперь от верхнего правого угла отложим высоту параллелограмма, после — ширину. Затем снова высоту, и снова ширину. От полученных точек проведем перпендикулярные линии к противоположной стороне, которые будут равны длине параллелограмма. Таким образом, мы получили 4 грани фигуры. Осталось еще 2 .
5. Над вторым прямоугольником справа дочертим ещё два снизу и сверху. В этом случае от второй отметки справа, которую мы делали в пункте 4, проведем перпендикуляр вверх равный высоте фигуры. Тоже самое повторим из второй отметки. Соединим перпендикуляры отрезком, равным ширине параллелограмма. Аналогичным методом построим нижний прямоугольник на противоположной стороне.
6. Для того, чтобы было легче склеивать параллелепипед из бумаги, добавим к чертежу дополнительные «крылышки», как указано на рисунке.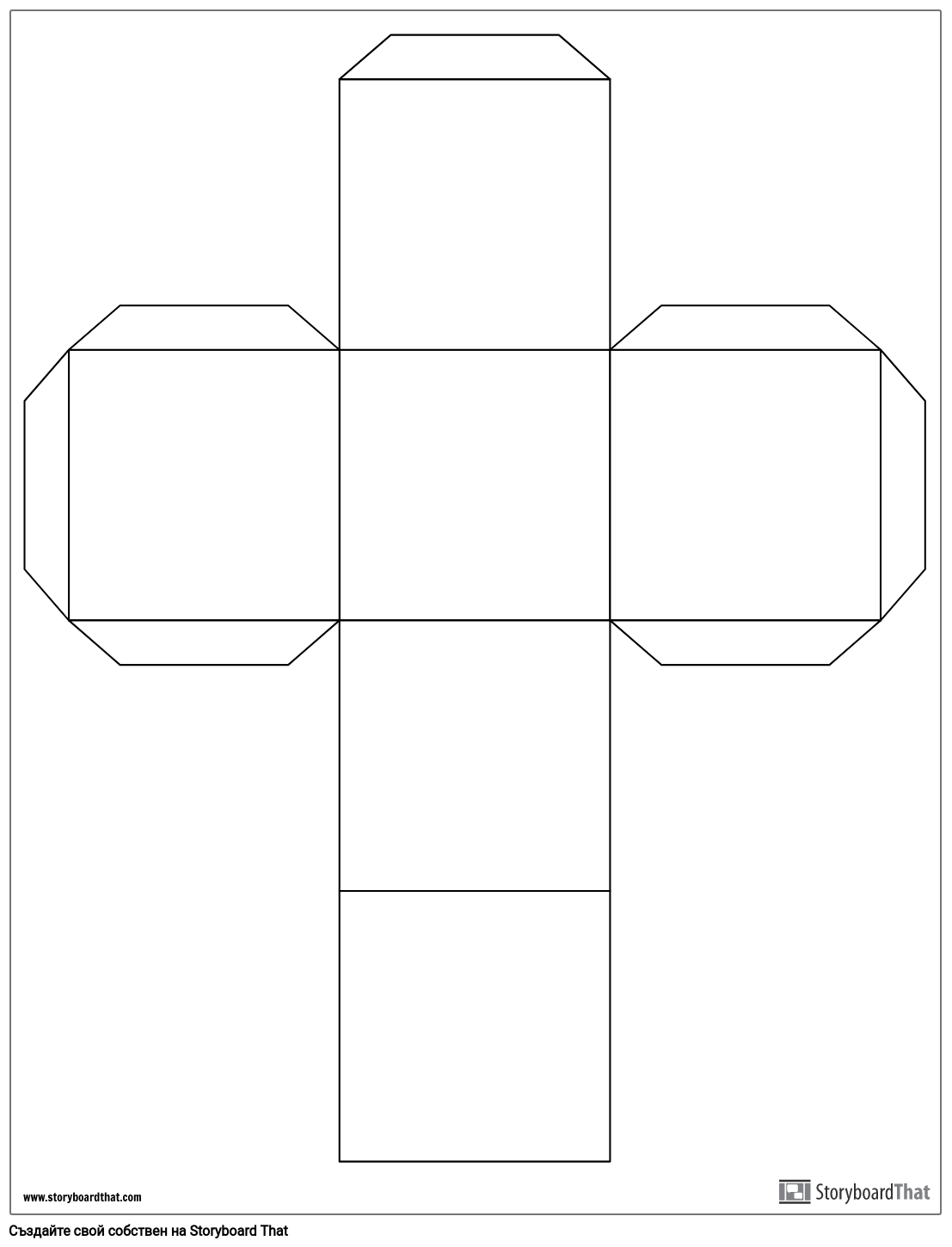 Их ширина должна быть около 1.5 см. Также необходимо сделать им скошенные углы (45 градусов), чтобы при склеивании они не выглядывали наружу.
Их ширина должна быть около 1.5 см. Также необходимо сделать им скошенные углы (45 градусов), чтобы при склеивании они не выглядывали наружу.
Итак, развертка параллелепипеда из бумаги готова. Важно, чтобы все детали чертежа были ровными и строго измеренными, иначе фигура не склеится ровно и будет кривой.
7. Вырежем заготовку и согнем её по всем линиям так, чтобы наши боковые грани соприкасались, а верхний и нижний прямоугольники стали «дном» и «крышкой» фигуры.
8. Смажем дополнительные «крылышки» клеем и соберем параллелепипед, заправив их внутрь. Подождем, пока клей высохнет.
Если вы освоили изготовление данной фигурки, можно приступить к собиранию наклонного параллелепипеда из бумаги, гранями которого являются остроугольные ромбы.
в интернете есть описание как сделать фигуру.Прилагаю схему,по черным и пунктирным линиям делают перегиб.
Собственно, ничего нового я тут не расскажу после такого огромного количества блестящих ответов. Поэтому я лучше покажу))
Ведь на пальцах такое не объяснишь :
Кстати, что особенно забавно, в детстве-то нас всех учили на уроках труда делать нечто подобное, но все как-то благополучно позабылось .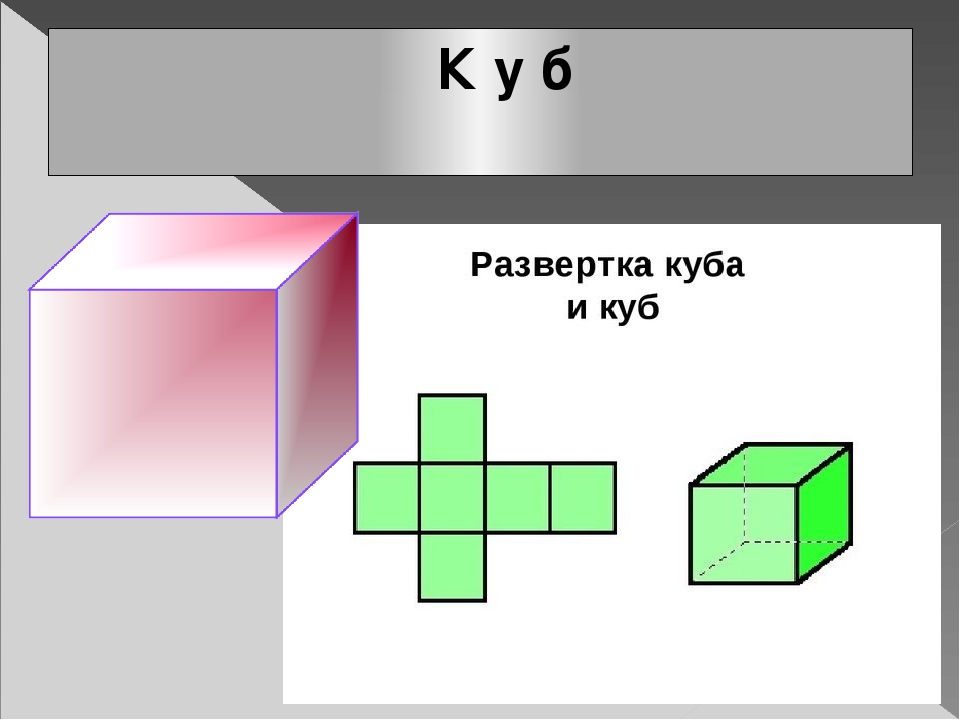 Хотя, вещи-то, по сути, элементарные.
Хотя, вещи-то, по сути, элементарные.
Я вот, например, совсем недавно не могла сообразить, как конверт из бумаги склеить, не прибегая к помощи Интернета)
На самом деле сделать параллелепипед и бумаги очень просто. Для это процедуры нужна бумага (что вполне понятное дело), ножницы, и обычный клей который сможет склеить бумагу. И все что нужно сделать, это посмотреть на схему ниже, и по ней вырезать похожую конструкцию и бумаги, после чего согнуть в нужных местах, и склеить ушки. Вот и все дела.
Для того чтобы сделать параллелепипед из бумаги своими руками вам потребуется следующее:
ножницы, линейка, карандаш, лист плотной бумаги и вот эта схема.
Вырезаем из бумаги вот такую деталь и при помощи клея ПВА и кисточки склеиваем, и получаем аккуратный и ровный параллелепипед.
Параллелепипед бывает прямоугольный и обычный. Рассмотрим, как можно научиться делать любые параллелепипеды, то есть с любым углом.
Сначала вычерчиваем на бумаге боковую сторону параллелепипеда, то есть ту, у которой может быть острый угол (на рисунке обозначено как a ). Вычерчиваем такую, какая нам нужна. Затем подкладываем под эту бумагу ещ один лист, то есть чтобы получилась двойная бумага. Легче даже сначала сложить лист бумаги пополам, а потом уже чертить. Затем вырезаем эту сторону. Так как у нас был двойной лист, то получилось сразу две одинаковых четыреугольных фигуры.
Вычерчиваем такую, какая нам нужна. Затем подкладываем под эту бумагу ещ один лист, то есть чтобы получилась двойная бумага. Легче даже сначала сложить лист бумаги пополам, а потом уже чертить. Затем вырезаем эту сторону. Так как у нас был двойной лист, то получилось сразу две одинаковых четыреугольных фигуры.
Затем на одинарной бумаге вычерчиваем выкройку b . Она должна быть с прямыми углами. Е стороны должны быть равны тем сторонам боковых поверхностей, как обозначено на рисунке. Одинаковые стороны обозначены одинаковыми линиями.
Затем обводим эту фигуру линией с отступом, чтобы начертить линию сгиба, которая будет промазываться клеем. Затем вырезаем эту фигуру, чтобы получилось как на рисунке b . Затем складываем две дальние стороны этой выкройки и склеиваем их чтобы фигура сомкнулась. Предварительно перед этим складываем все части сгибов, чтобы они стали угловатые. Затем промазываем части выкройки b , выделенные под клей. И прикладываем к обоим сторонам обе a части.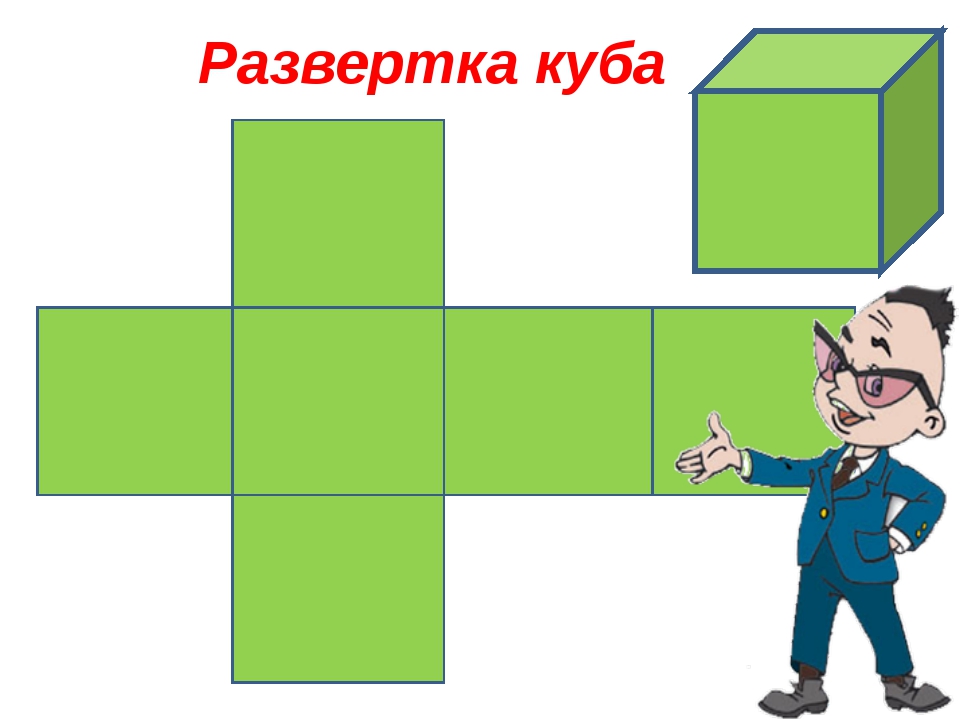
Параллелепипед готов.
Размеры на приведнном рисунке схематичны, вообщем их не нужно выводить на принтер и использовать в качестве выкройки, так как они рисовались в Пеинте, а не по размерам.
Для того, чтобы сделать параллелепипед из бумаги, нужно взять бумагу поплотнее, чтобы готовая уже склеенная модель хорошо держала форму. Изготовить ее очень просто по приведенным в интернете схемам, которых там великое множество. Нужно только правильно учесть все размеры сторон (длину, ширину, высоту) и выполнить ровно все сгибы, чтобы у готового параллелепипеда не было перекосов и прочих дефектов при сборке и склеивании.
Вот так выглядит схема:
Сделать такую коробочку из картонной бумаги очень легко.Для этого нам понадобится лист картона (любого цвета), ножницы и клей. Конечно проще всего сделать параллелепипед по схеме, чем читать долгие объяснения как именно сделать, поэтому ниже привожу схемку:
Параллелепипед из бумаги сделать очень просто. Главное, чтобы была схема, остальное будет уже делом техники.
Главное, чтобы была схема, остальное будет уже делом техники.
Итак вырезаем основу из листа бумаги, как указано на схеме. Далее складываем в тех местах, где прочерчены черные линии. После этого склеиваем наш параллелепипед при помощи канцелярского клея или клея ПВА.
Я не буду добавлять видео, как делать параллелепипед, так как для этого нужна только схема на рисунке. Ведь он делается очень просто. Даже первоклашка сможет его слепить из бумаги, если будет макет или пример.
Вот он, этот пример, внизу.
Сделать параллелепипед из бумаги не составит большого труда. Берем чистый лист бумаги, линейку, карандаш и чертим на бумаге таким вот образом:
Затем, сгибаем по пунктирным линиям, склеиваем канцелярским клеем и получаем вот такой параллелепипед:
Как сделать параллелепипед из бумаги? Схем достаточно много,даже с указанием места сгиба и прочих деталей.Вот, к примеру прямоугольный параллелепипед, который легко можно смастерить вот таким методом:
Склеивать удобно, да и практично!
Во время игры с ребенком разнообразными геометрическими фигурами, вы способствуете тому, чтобы у него развивалось пространственное мышление и воображение.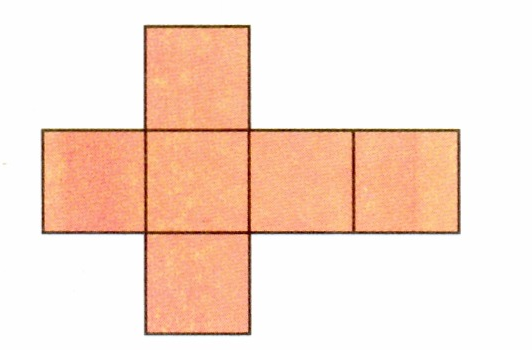 Малыш начинает понимать разнообразие форм различных поверхностей. Круглый или прямоугольный — это какой? Кубический или квадратный — это как? Отвечая своему чаду на различные вопросы, вы помогаете ему представлять и визуализировать разнообразие геометрических форм.
Малыш начинает понимать разнообразие форм различных поверхностей. Круглый или прямоугольный — это какой? Кубический или квадратный — это как? Отвечая своему чаду на различные вопросы, вы помогаете ему представлять и визуализировать разнообразие геометрических форм.
Благодаря этому, на уроках геометрии он сможет без труда усваивать учебный материал, решая задачи и доказывая теоремы. Одной из первых фигур, с которыми знакомят детей в школе, является параллелепипед. Для того, чтобы легче ее представлять и понять ее закономерности, предлагаем изготовить ее в качестве поделки.
Как сделать параллелепипед из бумаги вместе со своим ребенком.
Для этого нам понадобится:
- плотная бумага;
- линейка;
- ножницы;
- карандаш;
- клей ПВА.
Параллелепипед имеет в своем составе 6 граней, из которых каждая являет собой прямоугольник. В связи с этим, наша развертка будет иметь в своем составе 6 прямоугольников, которые будут находиться в одной плоскости.
Как сделать параллелепипед из бумаги поэтапно:
1. Сначала следует определить нужные величины фигуры: ширину, длину и высоту. От них напрямую будет зависеть ее размер.
2. Чертим схему параллелепипеда на бумаге. Которая должна быть достаточно плотной, чтобы не намокать от клея и хорошо держать форму.
3.Расчерчиваем прямую горизонтальную линию. Ее длина должна ровняться сумме ширины и высоты, умноженные на 2. После этого из каждого конца опускаем перпендикуляр, который по размерам равняется длине самой фигуры. Между ними проводим линию, параллельную той, что поводили в начале.
4. От верхнего угла справа откладываем высоту фигуры, потом — ширину. Повторяем эту процедуру еще раз. От точек, которые получили, поводим перпендикуляры к противоположным сторонам. В результате мы получаем 4 грани фигуры.
5.Над вторым прямоугольником, тем, что справа, дочерчиваем еще два — сверху и снизу. От отметки, которую мы делали в четвертом пункте, проведем перпендикуляр вверх по высоте. То же самое повторяем из второй отметки. Соединяем перпендикуляры прямым отрезком.
6.Чтобы чертеж было легче склеивать, добавляем к нему дополнительные элементы, как показывается на рисунке. Их можно сделать шириной 1,5 см. Так же нужно делаем у них скошенные углы, во избежание их выглядывания с внешних сторон. Развертка параллелепипеда готова!
Подробнее разобраться, как сделать параллелепипед из бумаги, помогут фото.
Следует отметить, чтобы параллелепипед получился ровным и правильным, нужно следить за тем, чтобы линии на макете были правильно проведены и строго измерены. В противном случае фигура получится геометрически не четкой.
Осталось только вырезать заготовку и согнуть по всем линиям, чтобы боковые грани соприкасались. Обработать специально предусмотренные выступающие элементы клеем и собрать параллелепипед.
Как сделать кормушки из пластиковых бутылок своими руками – фото, видео
Птица из пластиковой бутылки своими руками – фото, как сделать Пингвин из пластиковой бутылки своими руками – фото, видео как сделать
🛠 Развёртки геометрических фигур 👈
Большой выбор развёрток простых геометрических фигур.
Первое знакомство детей с бумажным моделированием всегда начинается с простых геометрических фигур, таких как кубик и пирамида. Не у многих получается склеить кубик с первого раза, иногда требуется несколько дней, чтобы сделать поистине ровный и безупречный куб. Более сложные фигуры цилиндр и конус требуют в несколько раз больше усилий нежели простой кубик. Если вы не умеете аккуратно клеить геометрические фигуры, значит и за сложные модели вам ещё рано браться. Займитесь сами и научите своих детей клеть эти «азы» моделирования по готовым развёрткам.
Для начала я, конечно же, предлагаю научиться клеить обычный кубик. Развёртки сделаны для двух кубиков, большого и маленького. Более сложной фигурой является маленький кубик потому, как клеить его сложнее, чем большой.
Итак, начнём! Скачайте развёртки всех фигур на пяти листах и распечатайте на плотной бумаге. Перед тем, как печатать и клеить геометрические фигуры обязательно ознакомьтесь со статьёй о том, как выбрать бумагу и как вообще правильно вырезать, сгибать и клеить бумагу.
Для более качественной печати советую использовать программу AutoCAD, и даю вам развёртки для этой программы, а также читайте, как распечатывать из автокада. Вырежьте развёртки кубиков с первого листа, по линиям сгиба обязательно проведите иголкой циркуля под железную линейку, чтобы бумага хорошо сгибалась. Теперь можно начинать клеить кубики.
Для экономии бумаги и на всякий пожарный я сделал несколько развёрток маленького кубика, мало ли вам захочется склеить не один кубик или что-то не получится с первого раза. Ещё одна несложная фигура это пирамида, её развёртки найдёте на втором листе. Подобные пирамиды стоили древние египтяне, правда не из бумаги и не таких маленьких размеров 🙂
А это тоже пирамида, только в отличие от предыдущей у неё не четыре, а три грани.
Развёртки трёхгранной пирамиды на первом листе для печати.
И ещё одна забавная пирамидка из пяти граней, её развёртки на 4-ом листе в виде звёздочки в двух экземплярах.
Далее шестигранник, склеить его будет ещё проще, чем пирамиды. Развёртки шестигранника на первом листе.
Более сложная фигура это пятигранник, хотя пятигранник сложнее начертить, нежели склеить.
Развёртки пятигранника на втором листе.
Вот мы и добрались до сложных фигур. Теперь придётся поднапрячься, склеить такие фигуры нелегко! Для начала обычный цилиндр, его развёртки на втором листе.
А это более сложная фигура по сравнению с цилиндром, т.к. в её основании не круг, а овал.
Развёртки этой фигуры на втором листе, для овального основания сделано две запасных детали.
Чтобы аккуратно собрать цилиндр его детали нужно клеить встык. С одной стороны дно можно приклеить без проблем, просто поставьте на стол заранее склеенную трубку, положите на дно кружок и залейте клеем изнутри. Следите, чтобы диаметр трубы и круглого дна плотно подходили друг к другу, без щелей, иначе клей протечёт и всё приклеится к столу. Второй кружок приклеить будет сложнее, поэтому приклейте внутри вспомогательные прямоугольники на расстоянии толщины бумаги от края трубы. Эти прямоугольники не дадут упасть основанию внутрь, теперь вы без проблем приклеете кружок сверху.
Цилиндр с овальным основанием можно клеить также как и обычный цилиндр, но он имеет меньшую высоту, поэтому тут проще вставить внутрь гармошку из бумаги, а наверх положить второе основание и по краю приклеить клеем.
Теперь очень сложная фигура – конус. Его детали на третьем листе, запасной кружок для днища на 4-ом листе. Вся сложность склеивания конуса в его острой вершине, а потом ещё будет очень сложно приклеить дно.
Сложная и одновременно простая фигура это шар. Шар состоит из 12-ти пятигранников, развёртки шара на 4-ом листе. Сначала клеится две половинки шара, а потом обе склеиваются вместе.
Довольно интересная фигура – ромб, её детали на третьем листе.
А теперь две очень похожие, но совершенно разные фигуры, их отличие только в основании.
Когда склеите эти обе фигуры, то не сразу поймёте, что это вообще такое, они получились какие-то совсем невосприимчивые.
Ещё одна интересная фигурка это тор, только он у нас очень упрощён, его детали на 5-ом листе.
И наконец, последняя фигура из равносторонних треугольников, даже не знаю, как это назвать, но фигура похожа на звезду. Развёртки этой фигуры на пятом листе.
На сегодня это всё! Я желаю вам успехов в этой нелёгкой работе!
Как в Word придать изображению форму любой фигуры
Как в Word придать изображению форму любой фигуры
Мы уже говорили о том, как нам обрезать изображение по контуру круга и другим контурам. Продолжим начатый разговор. И сегодня мы, как говорят, «копнём глубже».
Изображению, как правило, прямоугольной формы, мы можем придать абсолютно любую другую форму. Это могут быть формы не только геометрических фигур, таких как: круг, треугольник, ромб, многоугольник и многие другие. Мы можем придать изображению форму какого-то цветка, листа какого-то дерева, чайника, самолёта, автомобиля, женского силуэта, чернильной кляксы, какой-то птицы и т.д.
Пожалуй, самым трудным в этом процессе является создание самой этой сложной формы или фигуры, ну или контура.
Предположим, что мы решили придать изображению форму морской ракушки:
В данном случае, процесс создания контура облегчается тем, что ракушка находится на прозрачном фоне и очень контрастирует с листом Word залитым градиентом:
После того как мы поместили изображение ракушки на лист обратимся к верхнему меню, раскрыв вкладку «Вставка», в которой нас интересует функционал «Фигуры»:
Щелчком левой кнопки мыши раскроем содержание данного функционала и выберем инструмент «Кривая» (рисование кривой линии). Мы выбрали именно этот инструмент потому, что при создании сложного контура ракушки работать именно этим инструментом наиболее удобно:
Начав создавать контур ракушки (обводить) мы почувствуем, что линия, которую мы рисуем, словно магнитом притягивается к краям ракушки.
После того как мы выбрали инструмент «Кривая» курсор мыши принял вид крестика — можем приступать к созданию контура. Чтобы начать рисовать нужно один раз щёлкнуть левой кнопкой мыши. Начав обводить ракушку, и достигая изгибов, нам необходимо делать щелчки левой кнопкой мыши, устанавливая этими самыми щелчками невидимые нашим глазам опорные точки. Частые щелчки облегчат процесс рисования линии контура. Начать обводить ракушку можно с любого места. Я начну с этой точки:
Для удобства и точности лучшим будет увеличить масштаб видимости. Сделать это можно раскрыв вкладку «Вид» верхнего меню и выбрав опцию «Масштаб». Данная опция наделена возможностью делать индивидуальные настройки масштаба.
И вот что у нас должно получаться:
Обводя ракушку, мы должны соединить начальную и конечную точки линии контура, получив в результате, нужный нам замкнутый контур ракушки:
Как только мы замкнули контур, Word автоматически залил его цветом, создав, по сути, фигуру. Если заливка цветом нам не нужна, удалим её, а также приведём в соответствие масштаб видимости и поправим контур в том месте, где я специально допустил неточность обводки — на неё указывает стрелка на картинке выше.
Начнём с удаления заливки. Обратимся к верхнему меню и если появившаяся вкладка «Формат» не раскрыта, то раскроем её. Вкладка «Формат» функционала «Средства рисования» появляется в верхнем меню тогда, кода фигура выделена маркерами. Для выделения фигуры нужно сделать один щелчок левой кнопкой мыши, находясь курсором на теле фигуры.
Итак, вкладка «Формат» развёрнута, и мы обращаемся к опции «Заливка фигуры», где делаем выбор варианта «Нет заливки»:
Теперь поправим, созданный нами контур ракушки.
Если выделение контура маркерами сбросилось, то щелчком левой кнопки мыши восстановим его, наведя курсор на линию контура, а затем обратимся к инструменту «Изменить фигуру» опции «Начать изменение узлов», который расположен во вкладке «Формат» функционала «Средства рисования»:
После такого нашего выбора весь контур покрылся узловыми точками:
Для удобства вновь увеличим масштаб видимости и приступим к выравниванию контура, приводя его в полное соответствие с контуром оригинального изображения ракушки. Я увеличил масштаб видимости до 500%.
Наша работа по выравниванию контура заключается в том, что мы, хватая мышью (нажимаем и удерживаем левую кнопку) то одну то другую узловые точки контура, подтягиваем (перемещаем) их к краю оригинального изображения ракушки до полного их совмещения. Хватать и тянуть можно и красную линию, соединяющую узловые точки:
А также соединять друг с другом и сами узловые точки.
После того как мы привели в соответствие, созданный нами контур с контуром ракушки, изображение ракушки можно удалить. Это не составит большого труда, так как мы уже удалили заливку фигуры цветом, выбрав вариант «Нет заливки», то есть наша фигура прозрачна и имеет лишь видимый синего цвета контур.
Наведём курсор мыши на ракушку и щёлкнем левой кнопкой мыши. Ракушку захватили маркеры выделения (трансформирования):
Теперь нажмём клавишу «Delete» и изображение ракушки исчезнет:
Теперь переходим непосредственно к работе с самим изображением, которое и примет форму ракушки. Всё что нам нужно сделать, так это залить нашу прозрачную фигуру, имеющую только синий контур, изображением, ну или говоря иначе поместить в фигуру изображение. Когда мы это сделаем, изображение не выйдет за границы контура.
Приступим.
Наведём курсор мыши на линию синего контура в любом месте и сделаем один щелчок левой кнопкой мыши для выделения. Вместе с выделением уже нашей фигуры «Ракушка», в верхнем меню появится вкладка «Формат» функционала «Средства рисования». Щелчком левой кнопки мыши раскроем её содержание и обратимся к опции «Заливка фигуры»:
Где выберем вариант заливки «Рисунок»:
После выбора варианта заливки откроется окно операционной системы, и мы выберем нужное изображение из собственных папок или других библиотек. Выбранное изображение окажется внутри нашей фигуры «Ракушка», а в верхнем меню появится другая вкладка «Формат», относящаяся к функционалу «Работа с рисунками»:
Наличие в верхнем меню двух вкладок «Формат» различных функционалов, содержащих различные опции и инструменты, позволяет редактировать как саму фигуру, так и изображение внутри фигуры, применяя различные эффекты:
Помимо применения эффектов можно менять положение изображения внутри фигуры — перемещать изображение вправо, влево, вверх и вниз; расширить или сузить изображение. Всё это возможно делать с помощью двух инструментов: «Заливка» и «Обрезка».
Получить доступ к опциям этих инструментов мы можем, раскрыв одну из двух вкладок «Формат».
Давайте сначала раскроем вкладку «Формат» функционала «Средства рисования» и в нижнем правом углу раздела «Стили фигур» щёлкнем мышью по маленькой стрелочке:
Перед нами откроется диалоговое окно «Формат рисунка», в котором и находятся инструменты «Заливка» и «Обрезка». Обычным щелчком мыши выберем сначала инструмент «Заливка» и в правой части диалогового окна появятся опции данного инструмента, среди которых и нужные нам опции настройки перемещения изображения:
Щёлкая кнопками-стрелками, мы и воздействуем на изображение. Те изменения, которые будут происходить, отличаются от тех, которые произойдут при воздействии на изображение при выборе инструмента «Обрезка»:
Эти отличия нужно иметь в виду при редактировании изображения.
Если же мы развернём содержание вкладки «Формат» функционала «Работа с рисунками», то вызвать данное диалоговое окно «Формат рисунка» можно щелчком левой кнопки мыши по стрелочке в нижнем правом углу раздела «Стили рисунков»:
Вызвать данное диалоговое окно возможно и третьим способом.
Выделив нашу фигуру, залитую изображением и, находясь курсором внутри фигуры, мы делаем щелчок правой кнопкой мыши, и в появившемся перечне опций выбираем опцию «Формат фигуры»:
Конечно же, мы можем создавать свои собственные фигуры, выбрав удобный инструмент рисования в функционале «Фигуры», не прибегая к обводке каких-то объектов на сторонних изображениях:
Оставить комментарий
Гиперкуб
ГиперкубЕщё когда я был студентом-первокурсником у меня с одним моим одногруппником вышел горячий спор. Он говорил, что четырёхмерный куб представить нельзя ни в каком виде, а я уверял, что его можно представить достаточно отчётливо. Тогда я даже сделал из скрепок проекцию гиперкуба на наше трёхмерное пространство… Но давайте обо всём по-порядку.
Что такое гиперкуб и четырёхмерное пространство
В нашем привычном пространстве три измерения. С геометрической точки зрения это значит, что в нём можно указать три взаимно-перпендикулярных прямых. То есть для любой прямой можно найти вторую, перпендикулярную первой, а для пары можно найти третью прямую, перпендикулярную двум первым. Найти четвёртую прямую, перпендикулярную трём имеющимся, уже не удастся.
Четырёхмерное пространство отличается от нашего только тем, что в нём есть ещё одно дополнительное направление. Если у вас уже есть три взаимно перпендикулярные прямые, то вы можете найти четвёртую, такую, что она будет перпендикуляра всем трём.
Гиперкуб это просто куб в четырёхмерном пространстве.
Можно ли представить четырёхмерное пространство и гиперкуб?
Этот вопрос сродни вопросу: «можно ли представить Тайную Вечерю, посмотрев на одноимённую картину (1495-1498) Леонардо да Винчи (1452-1519)?»
С одной стороны, вы конечно не представите то, что видел Иисус (он сидит лицом к зрителю), тем более вы не почувствуете запаха сада за окном и вкуса еды на столе, не услышите пения птиц… Вы не получите полного представления о происходившем в тот вечер, но нельзя сказать, что вы не узнаете ничего нового и что картина не представляет никакого интереса.
Аналогичная ситуация и с вопросом о гиперкубе. Полностью представить его нельзя, но можно приблизиться к пониманию, каков он.
Построение гиперкуба
0-мерный куб
Начнём с начала — с 0-мерного куба. Этот куб содержит 0 взаимно перпендикулярных граней, то есть это просто точка.
1-мерный куб
В одномерном пространстве у нас есть только одно направление. Сдвигаем точку в этом направление и получаем отрезок.
Это одномерный куб.
2-мерный куб
У нас появляется второе измерение, сдвигаем наш одномерный куб (отрезок) в направлении второго измерения и получаем квадрат.
Это куб в двумерном пространстве.
3-мерный куб
С появлением третьего измерения поступаем аналогично: сдвигаем квадрат и получаем обычный трёхмерный куб.
4-мерный куб (гиперкуб)
Теперь у нас появилось четвёртое измерение. То есть в нашем распоряжении имеется направление, перпендикулярное всем трём предыдущим. Воспользуемся им точно так же. Четырёхмерный куб будет выглядеть вот так.
Естественно, трёхмерный и четырёхмерный кубы нельзя изобразить на двумерной плоскости экрана. То, что нарисовал я — это проекции. О проекциях мы поговорим чуть позже, а пока немного голых фактов и цифр.
Количество вершин, рёбер, граней
| Характеристики кубов различной размерности | |||
|---|---|---|---|
| размерность пространства | количество вершин | количество рёбер | количество граней |
| 0 (точка) | 1 | 0 | 0 |
| 1 (отрезок) | 2 | 1 | 2 (точки) |
| 2 (квадрат) | 4 | 4 | 4 (отрезки) |
| 3 (куб) | 8 | 12 | 6 (квадраты) |
| 4 (гиперкуб) | 16 | 32 | 8 (кубы) |
| N (общая формула) | 2N | N·2N-1 | 2·N |
Обратите внимание, что гранью гиперкуба является наш обычный трёхмерный куб. Если внимательно посмотреть на рисунок гиперкуба, то можно действительно найти восемь кубов.
Проекции и зрение жителя четырёхмерного пространства
Несколько слов о зрении
Мы живём в трёхмерном мире, но видим мы его двумерным. Это связано с тем, что сетчатка наших глаз расположена в плоскости, имеющей только два измерения. Именно поэтому мы способны воспринимать двумерные картины и находить их похожими на реальность. (Конечно, благодаря аккомодации, глаз может оценить расстояние до объекта, но это уже побочное явление, связанное с оптикой, встроенной в наш глаз.)
Глаза жителя четырёхмерного пространства должны иметь трёхмерную сетчатку. Такое существо может сразу увидеть трёхмерную фигуру полностью: все её грани и внутренности. (Точно так же мы можем увидеть двумерную фигуру, все её грани и внутренности.)
Таким образом, с помощью наших органов зрения, мы не способны воспринять четырёхмерный куб так, как его воспринимал бы житель четырёхмерного пространства. Увы. Остаётся только уповать на мысленный взор и фантазию, которые, к счастью, не имеют физических ограничений.
Тем не менее, изображая гиперкуб на плоскости, я просто вынужден делать его проекцию на двумерное пространство. Учитывайте это обстоятельство, при изучении рисунков.
Пересечения рёбер
Естественно, ребра гиперкуба не пересекаются. Пересечения появляются только на рисунках. Впрочем, это не должно вызывать удивления, ведь рёбра обычного куба на рисунках тоже пересекаются.
Длины рёбер
Стоит отметить, что все грани и рёбра четырёхмерного куба равны. На рисунке они получаются не равными только потому, что расположены под разными углами к направлению взгляда. Однако можно развернуть гиперкуб так, что все проекции будут иметь одинаковую длину.
Кстати, на этом рисунке отчётливо видны восемь кубов, являющихся гранями гиперкуба.
Гиперкуб внутри пустой
В это трудно поверить, но между кубами, ограничивающими гиперкуб, заключено некоторое пространство (фрагмент четырёхмерного пространства).
Чтобы это лучше понять, давайте рассмотрим двумерную проекцию обычного трёхмерного куба (я специально сделал её несколько схематичной).
Можно ли по ней догадаться, что внутри куба есть некоторое пространство? Да, но только применив воображение. Глаз этого пространства не видит. Это происходит потому, что рёбра, расположенные в третьем измерении (которое нельзя изобразить на плоском рисунке), теперь превратились в отрезки, лежащие в плоскости рисунка. Они больше не обеспечивают объём.
Квадраты, ограничивающие пространство куба, наложились друг на друга. Но можно представить, что в исходной фигуре (трёхмерном кубе) эти квадраты располагались в разных плоскостях, а не один поверх другого в одной плоскости, как это получилось на рисунке.
Точно так же дело обстоит и с гиперкубом. Кубы-грани гиперкуба на самом деле не накладываются, как это кажется нам на проекции, а располагаются в четырёхмерном пространстве.
Развёртки
Итак, житель четырёхмерного пространства может увидеть трёхмерный объект одновременно со всех сторон. Можем ли мы одновременно со всех сторон увидеть трёхмерный куб? Глазом — нет. Но люди придумали способ, как изобразить на плоском рисунке все грани трёхмерного куба одновременно. Такое изображение называется развёрткой.
Развёртка трёхмерного куба
Как образуется развёртка трёхмерного куба все наверно знают. Этот процесс показан на анимации.
Для наглядности края граней куба сделаны полупрозрачными.
Следует отметить, что мы способны воспринять эту двумерную картинку только благодаря воображению. Если рассмотреть фазы разворачивания с чисто двумерной точки зрения, то процесс будет казаться странным и совсем не наглядным.
Он выглядит, как постепенное появление сперва очертаний искажённых квадратов, а потом их расползание на свои места с одновременным принятием необходимой формы.
Если смотреть на разворачивающийся куб в направлении одной из его граней (с этой точки зрения куб выглядит как квадрат), то процесс образования развёртки ещё менее нагляден. Всё выглядит как выползание квадратов из начального квадрата (не развёрнутого куба).
Но не наглядна развёртка только для глаз. Как раз благодаря воображению из неё можно почерпнуть много информации.
Развёртка четырёхмерного куба
Сделать анимированный процесс разворачивания гиперкуба хоть сколько нибудь наглядным просто невозможно. Но этот процесс можно представить. (Для этого надо посмотреть на него глазами четырёхмерного существа.)
Развёртка выглядит так.
Здесь видны все восемь кубов, ограничивающих гиперкуб.
Одинаковыми цветами покрашены грани, которые должны совместиться при сворачивании. Серыми оставлены грани для которых парных не видно. После свёртки самая верхняя грань верхнего куба должна совместиться с нижней гранью нижнего куба. (Аналогично сворачивается развёртка трёхмерного куба.)
Обратите внимание, что после свёртки все грани восьми кубиков придут в соприкосновение, замкнув гиперкуб. И наконец, представляя процесс свёртывания, не забывайте, что при свёртывании происходит не наложение кубов, а оборачивание ими некой (гиперкубической) четырёхмерной области.
Сальвадор Дали (1904-1989) много раз изображал распятие, а кресты фигурируют в очень многих его картинах. На картине «Распятие» (1954) используется развёртка гиперкуба.
Пространство-время и евклидово четырёхмерное пространство
Надеюсь, что вам удалось представить гиперкуб. Но удалось ли вам приблизиться к пониманию, как устроено четырёхмерное пространство-время в котором мы живём? Увы, не совсем.
Здесь мы говорили об евклидовом четырёхмерном пространстве, но пространство-время обладает совсем другими свойствами. В частности, при любых поворотах отрезки остаются всегда наклонены к оси времени либо под углом меньше 45 градусов, либо под углом больше 45 градусов.
Свойствам пространства времени я посвятил серию заметок.
Отправить
Цилиндр, конус, шар, развёртка цилиндра и конуса
Цилиндр, конус и шар относятся к объемным (трехмерным) геометрическим фигурам вращения.
Объемные фигуры вращения (еще говорят — «тела», подразумевая объемность фигуры), как правило, образованы вращением плоской фигуры вокруг какой-то линии (прямой).
Так, цилиндр — это фигура, полученная от вращения прямоугольника вокруг одной из его сторон как оси; конус — вращением прямоугольного треугольника вокруг его катета как оси, шар — вращением полукруга вокруг его диаметра как оси.
Объемные фигуры бывают прямые (прямой цилиндр, прямой конус) и наклонные (наклонный цилиндр, наклонный конус), что зависит от вида той плоской геометрической фигуры, которая их образует.
В курсе математики для б класса рассматриваются только прямые цилиндры и конусы
.
Определение. Цилиндр — это тело (объемная геометрическая фигура), полученное вращением прямоугольника вокруг одной из его сторон как оси.
Определение. Конус (прямой) — это тело (объемная геометрическая фигура), полученное вращением прямоугольного треугольника вокруг его катета как оси.
Определение. Шар — это тело (объемная геометрическая фигура), полученное вращением полукруга вокруг его диаметра как оси.
Развертки цилиндра и конуса
Разверткой геометрической фигуры называется изображение плоскости, ограничивающей фигуру, в одной плоскости листа по размерам фигуры.
Развертка цилиндра приведена схематически.
Развертка конуса приведена схематически.
Площади боковой поверхности цилиндра и конуса
Правило. Площадь боковой поверхности цилиндра равна произведению длины окружности основания и высоты цилиндра.
где C — длина окружности, H — высота цилиндра, R — радиус окружности основания.
Правило. Площадь боковой поверхности конуса равна произведению половины длины окружности основания и образующей конуса.
где C — длина окружности основания, l — длина образующей конуса, R — радиус основания.
Площадь поверхности шара
Правило. Площадь поверхности шара равна учетверенной площади большого круга шара.
где R — радиус шара.
Объемы цилиндра, конуса и шара
Правило. Объем цилиндра равен произведению площади основания н высоты.
где R — радиус основания, H — высота цилиндра.
Правило. Объем конуса равен одной трети произведения площади основания и высоты конуса.
где R — радиус основания, H — высота конуса.
Правило. Объем шара равен четырем третям
произведения числа Пи на куб радиуса.
где R — радиус шара.
Атрибутов и сетей куба
Сводка
Учащиеся будут использовать свои знания об атрибутах кубиков, работать вместе в группах и находить как можно больше кубиков.
Материалы
| Важная книга Инструкции: | |
1.Сложите лист плотной бумаги размером 12 x 18 дюймов пополам по горизонтали, затем откройте его и снова положите горизонтально. | |
2. Далее снова сложите по вертикали 2 раза (сложите пополам и еще раз пополам) | |
3. Разложите один раз. Разрежьте сгиб до средней линии сгиба и раскройте бумагу. | |
4.Теперь сложите бумагу по горизонтали. | |
5. Сожмите концы к центру, загните и загните. | |
6. Буклет малый на 8 страниц.
| |
Способы использования книги: Самое важное о: 3-м классе, новом друге, с которым я познакомился, дробях, геометрических фигурах и т. Д.(Отличная идея при использовании атрибутов.) | |
Дополнительные ресурсы
Книги
- Важная книга Маргарет Уайз Браун ISBN: 0064432270
Фон для учителей
Куб состоит из шести квадратных граней, двенадцати ребер и восьми вершин. Когда квадратные грани куба разделены по краям и разложены плоско, они образуют двухмерную фигуру, называемую сеткой.Для куба существует одиннадцать различных сетей.
- Сетка — двухмерная фигура, которую можно сложить в трехмерную фигуру, является сеткой этой фигуры.
- Лицо — плоская фигура, служащая одной стороной твердой фигуры. Грани куба — квадраты.
- Вершина (вершины) — точка, в которой два отрезка, линии или лучи встречаются, образуя угол.
- Ребро — отрезок прямой, на котором встречаются две грани твердого тела.
Сегодня студенты будут использовать свои знания об атрибутах кубиков, работать вместе в группах и находить как можно больше способов сделать куб. Двумерный узор для трехмерной формы называется сеткой.
Студенты будут работать вместе в небольших группах, и каждая группа будет разного цвета. Они будут использовать ленту, чтобы соединить фигуры, которые складываются в куб.
Предполагаемые результаты обучения
1.Продемонстрировать положительное отношение к математике.
2. Научитесь решать математические задачи.
3. Рассуждайте математически.
Инструкционные процедуры
Приглашение к учебе
Выведите учащихся на площадку. Спросите: «Кто может сказать, что такое атрибут? Атрибут описывает что-то о предмете или человеке. Попросите ученика встать перед классом и назвать атрибут ребенка (цвет его волос, глаз, обуви, и т.п.). Сегодня мы узнаем об атрибутах куба.
Прочтите книгу « Важная книга » Маргарет Уайз Браун.
Скажите студентам, что, как детективы, они будут описывать атрибуты куба.
Инструкционные процедуры
- В качестве класса выберите в классе двух- или трехмерный объект (например, глобус или флаг). Попросите учащихся придумывать атрибуты, а учитель перечисляет атрибуты на доске.
- Поднимите куб и обсудите со студентами различные атрибуты куба, убедившись, что они называют «боковые» грани. Попросите учащихся записать атрибуты в своих математических журналах.
- Попросите учащихся осмотреть комнату и назвать предметы, имеющие форму куба. Проверьте заранее и убедитесь, что у вас есть хотя бы один или два кубических объекта в комнате! Если это не было затронуто, спросите учащихся, какие двухмерные формы составляют куб.
- Затем пройдитесь по атрибутам куба.Запишите их на доске. Попросите учащихся записать их в своих дневниках.
- Затем предложите учащимся объяснить, почему, по их мнению, форма куба важна. Попросите их придумать в реальной жизни предмет, имеющий форму куба, и перечислить его атрибуты. Попросите учащихся заполнить рабочий лист «Важная вещь». Заполнив лист, студенты могут составить буклет со своими атрибутами.
- Затем учащиеся работают в группах по четыре человека, используя двухдюймовые квадраты, чтобы создать как можно больше различных сеток для куба.Дайте каждой группе два набора по 6 штук, чтобы у каждого в группе была возможность опробовать свои идеи. Как только они подумают, что у них есть сеть, попросите их доказать, что она работает, скопировав сеть на 2-дюймовую сетку, вырезав ее и сложив в куб. Возможно, вы захотите показать всему классу несколько первых рабочих сетей, которые являются Вы можете принять участие в соревновании, чтобы не отвлекаться от учащихся. Группа с самыми разными сетками для куба становится победителем.
Закрытие
В математических журналах пусть ученики подходят к классу и записывают атрибуты сетей.
- Каждая сетка состоит из шести квадратов, которые при правильном сложении образуют шесть граней куба.
- Для каждой сети шесть граней соединены пятью ребрами Попросите учащихся поделиться и записать то, что они узнали о кубе.
- Кубики имеют двенадцать граней
- восемь вершин
- шесть граней
Оценка
- Ученики могут использовать миллиметровую бумагу, чтобы рисовать различные способы, которые они нашли для создания сети.
- Студент Важная книга о кубе.
- Записи в дневнике.
- Учащиеся создают буклет, демонстрирующий знание атрибутов куба.
Добавочные номера
Расширение учебной программы / адаптации / интеграция
- Отлично подходит для интеграции языковых навыков и письма в математику
Семейные связи
- Учащиеся отправляются на поиски «кубиков» у себя дома.
План оценки
Библиография
Основа исследования
Битти В., Коллинз Б. и Макиннес Б. (1997). Глубокое и поверхностное обучение: простая или упрощенная дихотомия? Бухгалтерское образование , 6 (1), 1-12.
Стихи глубокого обучения на поверхности или механическое заучивание имеют важное значение для учащихся, чтобы получить понимание для обучения.Процессы обучения студентов для глубокого обучения включают использование различных стилей обучения для улучшения личности студента.
Хартсхорн Р. и Борен С. (июнь 1990 г.). Практическое изучение математики: Использование манипуляторов. Вашингтон, округ Колумбия: Информационный центр ERIC по сельскому образованию и малым школам, ERIC Digest. (Номер услуги репродукции документов ERIC ED321967)
Активное участие в различных стилях обучения улучшит обучение студентов. Математика настолько абстрактна, что ученикам становится трудно ее понять.Следовательно, использование манипуляторов имеет важное значение для обучения.
Создано: 27.06.2006
Обновлено: 05.02.2018
109328
Коробок и эскизов | Формы | CBSE | Класс 5
Sweet Box
Рамя пошла за конфетами. Продавец взял вырез из бумаги и быстро сделал красивую розовую коробку для конфет!
- Посмотрите фото и сделайте коробку самостоятельно.Используйте вырез на стр. 201. Как быстро вы его сложите? Вернувшись домой, Рамя развернул коробку. Она убрала лишние откидные створки, чтобы вырез выглядел так
- Она сделала еще четыре формы. Каждую складываем по пунктирным линиям. Вы должны выяснить, из чего можно сделать коробку.
В этой главе основное внимание уделяется визуализации трехмерных форм и тому, как их можно представлен на бумаге (в 2-х измерениях).Используемое здесь представление — это сети (например, выше), планы планировки дома и перспективные чертежи.
Фигуры, складывающиеся в куб
Будда хочет сделать бумажный куб из прямоугольного листа. Он знает, что все грани куба — квадраты.
Он рисует две разные фигуры.
- Свернутся ли обе эти формы в куб ??
- Нарисуйте хотя бы еще одну фигуру, которая может складываться в куб.
- Какой будет площадь каждой грани куба?
- Нарисуйте одну фигуру, которая не складывается в куб.
- Посмотрите вокруг и обсудите, какие объекты вокруг вас выглядят как куб. Перечислите несколько.
Формы для открытого ящика
Помните головоломки с пятью квадратами в главе 3? Вы видели 12 различных форм, состоящих из пяти квадратов (стр. 46).
Если вырезать эти фигуры и сложить их, некоторые из них сложатся в открытую коробку (коробку без верха).
- Узнайте, какие из 8 других форм (на странице 46) можно сложить, чтобы получилась открытая коробка.
- Нарисуйте больше фигур, которые не складываются, чтобы получился открытый ящик.
Коробки и ящики
Все коробки не кубики. Вот несколько разных видов ящиков. Совместите фигуру слева с коробкой, в которую она складывается.
Создание мысленных образов форм — важная математическая способность. Детям понадобится много упражнений, чтобы визуализировать сетку ящика, думать как это выглядит в расплющенном состоянии, а также для проверки того, какие цепи (например, на стр. 126) не образуют короба.
Карты этажей
Для постройки дома сначала делается карта этажа. Вы когда-нибудь видели карту этажа? Вот карта этажа дома Вибхи. Он показывает, где в доме находятся окна и двери.
- Какая передняя сторона ее дома? Сколько окон на лицевой стороне?
По карте этажа мы не можем понять, как на самом деле выглядит ее дом и насколько высоко окна есть. Поэтому мы ищем особый способ нарисовать дом, который будет глубоким — показать длину, ширину и высоту.
Вот четыре глубоких чертежей домов —
- Какой из них является домом Вибхи?
- Почему три других глубоких рисунка не совпадают с картой этажа? Обсуждать.
Трехмерный перспективный рисунок был назван «глубоким рисунком», чтобы дети почувствовали необходимость изображать глубину. Они должны уметь видеть разницу между глубокими чертежами и планами компоновки.
Время практики- Посмотрите на эту карту этажа дома.Сделайте двери и окна по глубокому чертежу этого дома. Есть ли какие-нибудь окна, которые нельзя показать на глубоком чертеже? Обведите их на карте этажа.
- Попробуйте составить карту этажа собственного дома.
Глубокий рисунок куба
Сумитро и его друзья сделали глубокие рисунки куба. Это их рисунки.
- Какой из рисунков вам подходит? Обсуждать.
- Можете ли вы добавить несколько линий, чтобы сделать рисунок f) глубоким рисунком куба?
Головоломка
Простой способ нарисовать куб
Чанда хочет глубоко нарисовать этот куб.Вот так она рисует куб.
- Таким же образом сделайте глубокий рисунок коробки, которая выглядит следующим образом.
2D-представление 3D-объектов является условным и изучается детьми. через опыт. Здесь дается традиционный способ рисования куба.
Matchbox Play
Навин, Бхаскар и Пратигья построили этот мост из спичечных коробок.
Навин и Пратигья сделали чертежи моста.
- Если посмотреть на мост сверху, как он будет выглядеть? Выберите правильный рисунок ниже:
- Посмотрите на фото и попробуйте сделать глубокий рисунок этого моста.
- Сделайте чертежи, чтобы показать, как этот мост будет выглядеть
- Сверху
- Спереди
- сбоку
- Сделайте модель спичечного коробки, которая выглядит так. Также сделайте глубокий рисунок модели в блокноте.
- Сколько кубиков нужно, чтобы сделать эту интересную модель? Вот несколько рисунков модели. Отметьте правильный чертеж вида сверху буквой «T», а правильный чертеж вида сбоку — буквой «S».
Свалка геометрии: развернутые многогранники
Свалка геометрии: развернутые многогранникиРазвернутые многогранники
Обычный способ создания моделей многогранников — развернуть грани в виде плоский узор, вырежьте узор из бумаги и снова сложите.Всегда ли это возможно?- 85 складок латинского креста, E. Demaine et al.
- Примеры, Контрпримеры и результаты подсчета складок и развертываний между полигонами и многогранниками, Эрик Д. Демейн, Мартин Л. Демейн, Анна Любив, Джозеф О’Рурк, cs.CG/0007019.
- Найти все многогранники. Интернет-программное обеспечение Коичи Хираты для поиска всех способов склеивание ребер многоугольника так, чтобы он мог складываться в выпуклый многогранник.
- Флексагоны. Сложенные бумажные полиалмазы, которые можно «согнуть», чтобы показать различные наборы лица.Также Гарольд Документы Макинтоша о флексагоне, включая копии оригинальных документов Конрада-Хартлайна 1962 года, также отражено на сайте Эрика Демейна.
- Программа HyperGami для разворачивания многогранников, также описанная в это статья американского ученого.
- Кнотология. Как сложить правильные многогранники из сложенных полосок бумаги?
- MatHSoliD Java-анимация плоских разверток платоновых и архимедовых многогранников.
- Модели платоновых тел и родственные симметричные многогранники.
- Новое перспективные системы Дика Термеса, художник, рисующий вывернутые наизнанку сцены на сферах, создают иллюзию взгляда в отдельные маленькие миры. На его сайте также есть пример развернутого додекаэдра. вы можете распечатать, вырезать и сложить самостоятельно.
- Оригамический тетраэдр. На изображении ниже изображен способ создания пяти складок в виде 2-3-4 треугольника. так что он складывается в тетраэдр. Тоши Като спрашивает, можете ли вы сбросить карты треугольник в тетраэдр всего с тремя складками. Оказывается, есть уникальное решение, хотя многие тетраэдры могут иметь большее количество складок.
- Бумага модели многогранников.
- Пентамино проект месяца от Форума по геометрии. Составьте список пентамино; сложите их, чтобы получился куб; сыграйте в игру с пентамино. См. Также развёртывание полимино-куба протеона и Ливио Покрытый полимино куб Зукки.
- Плексагоны. Рон Эванс предлагает использовать поверхности из гофрированных шестиугольников в качестве модульные конструкции. Пол Бурк объясняет.
- Poly, условно-бесплатное ПО для Windows / Mac для изучения различных классов многогранников, включая Платоновы тела, Архимедовы твердые тела, твердые тела Джонсона и т. Д.Включает перспективные виды, Схемы Шлегеля и развернутые сети.
- Обычный Раскладки 4d многогранников. Анимация Java от Эндрю Веймхолта. Также включает несколько нестандартных политопов.
- Твердый объект, создающий аномальное изображение. Кокичи Сугихара делает модели иллюзий Эшера из сложенной бумаги. У него есть еще много чего, откуда этот, но, может быть, другие не в сети.
- Звездная пыль Пазлы-многогранники. Эта британская компания продает развернутые многогранные пазлы и космические фигуры (включая красивую модель Пена, заполняющая пространство Weaire-Phelan) на картоне, вырезать и построить самому.
- Стелла и Stella4d, Программное обеспечение Windows для визуализации правильных и полурегулярных многогранников и их звёздчатые формы в трёх и четырёх измерениях, трансформируя их друг в друга, рисуя развернутые сети для изготовление бумажных моделей и экспорт многогранников в различные пакеты 3D-дизайна.
- Странные развертывания выпуклых многогранников, Комей Фукуда, ETH Zurich.
- Пособие для учителя по построению икосаэдра в качестве классного проекта.
- мозаичный многогранники. Цветные развертывания Платоновых тел, готовые к напечатанная, вырезанная и сложенная Джилл Бриттон.
- Tobi Игрушки продать Vector Flexor, гибкий кубооктаэдрический каркас, и Сложить форму, визитную карточку оригами, которая складывается в тетраэдр, который можно используется как строительный блок для более сложных многогранников.
- Touch-3d, коммерческий программное обеспечение для разворачивания 3д моделей в плоские распечатки, которые нужно сложить обратно снова вверх для быстрого создания прототипов и макетов.
- Разворачивающиеся выпуклые многогранники. Со страниц геометрии Джеффа Эриксона.
- Анимация развертывания додекаэдра, Рик Мабри.
- Раскладывающиеся выпуклые многогранники. Екатерина Шевон обсуждает, всегда ли это возможно разрезать ребра выпуклого многогранника так, чтобы его граница развернулась в простой плоский многоугольник. Известные математические страницы Дэйва Русина включают еще одна статья Дж. О’Рурка по той же проблеме.
- Раскладывание некоторые классы ортогональных многогранников, Бидл, Демейн, Демейн, Любив, Овермарс, О’Рурк, Роббинс и Уайтсайдс, CCCG 1998.
- Раскладывание тессеракт. Питер Терни перечисляет 261 поликуб, которые могут быть сложенный в четырех измерениях, чтобы сформировать поверхность гиперкуба, и обеспечивает анимацию разворачивающегося процесса.
- Развертка морщинистые формы. Новости науки обсуждают недавний результат Демейна, Коннелли и Роута, что любой невыпуклый плоский многоугольник можно непрерывно развернуть в выпуклое положение.
- Когда может ли многоугольник складываться в многогранник? А. Любив и Дж. О’Рурк описывают алгоритмы нахождения складок, которые превращают развернутую бумажную модель многогранник в сам многогранник. Оказывается, знакомый узор крест-гексомино для складывания кубиков также можно использовать для складывания трех других многогранники с четырьмя, пятью и восемью сторонами.
Со свалки Геометрии,
вычислительный
указатели рекреационной геометрии.
Отправьте электронное письмо, если вы
знать о соответствующей странице, не указанной здесь.
Дэвид Эппштейн,
Теоретическая группа,
ICS,
Калифорнийский университет в Ирвине.
Полуавтоматический
фильтрованный
из общего исходного файла.
3D-фигуры и сети | SkillsYouNeed
На нашей странице, посвященной трехмерным формам, мы ввели трехмерные формы, называемые многогранниками , которые имеют несколько плоских поверхностей ( граней ), состоящих из двухмерных многоугольников , соединенных прямыми ребрами и острыми углами ( вершины ). ).
Полезным свойством этих твердых форм является то, что они могут быть описаны визуально в двух измерениях с помощью формы сетки .
Сеть в этом контексте не что иное, как рыболовная сеть или баскетбольная сетка! Это просто двухмерное изображение того, как выглядела бы трехмерная фигура, если бы все ее стороны были плоско сложены. Представьте, например, открытую картонную коробку.
2D-сетку можно сложить, чтобы получить 3D-форму.
Сетки кубиков и кубоидов
На диаграмме ниже вы можете видеть знакомые обозначения игральных костей, но это не трехмерный куб, как вы ожидали, а плоское двухмерное представление игральных костей.Вы можете вырезать его и склеить, чтобы получился куб:
Шесть отдельных квадратов с знакомыми точками игральных костей представляют собой сетку формы куба . Маленькие язычки по краям позволяют склеивать кубики.
Сетки для кубиков — нет одного ответа
Кубические сети — одни из самых простых для визуализации, и это забавный тест ваших пространственных навыков, чтобы увидеть, сколько вы можете создать.Фактически, существует 11-образных сеток, которые составляют куба.
На диаграмме ниже показано 16 различных вариантов расположения 6 квадратов, которые все выглядят так, как будто они могут быть кубическими сетками, но 6 из них — нет. Можете ли вы определить, какие сети куба являются действительными?
Ответ состоит в том, что 1, 4, 6, 7, 8, 9, 12, 13, 14 и 15 — все допустимые сети куба.
2, 3, 5, 10, 11 и 16 не могут образовать куб, и они не-сети . Отсутствует одна действительная сеть…. ты можешь это решить?
Это довольно сложно…
Теперь, когда вы начали упражняться в пространственных способностях с обычными кубами, сетку формы кубоида должно быть легче понять.
Кубоид похож на куб, но некоторые или все его стороны могут быть прямоугольными. Таким образом, сети имеют те же характеристики, что и у куба, но выглядят совершенно иначе.
Вот сетка из прямоугольного кубоида с длинами сторон 10см, 20см и 40см.
Найдите вершину (угол) кубовидной сети, отмеченную красной точкой.Снова используя свои пространственные навыки, можете ли вы определить, какие другие вершины, помеченные 1–6, будут соединяться с красной точкой, когда кубоид находится в своей трехмерной форме?
Nets может рассказать нам больше….
Теперь, когда мы знаем размеры сети, мы можем узнать другие свойства этого твердого тела, такие как его объем и площадь поверхности .
Объем кубоида рассчитывается как произведение его длины, ширины и высоты:
Длина × Ширина × Высота = 40 × 20 × 10 = 192
Таким образом, объем кубовидной формы равен 8000 см 3 или 8 литров.
Площадь поверхности — это общая площадь всех шести сторон, сложенных вместе.
У нас есть две стороны размером 20 × 40 см, 10 × 20 см и 10 × 40 см.
2 × 20 × 40 = 1600
2 × 10 × 20 = 200
и 2 × 10 × 40 = 800
16 + 200 + 800 = 2,800
Таким образом, кубовид имеет площадь поверхности 2800 см 2 или 0,28 м 2
Сети призм, пирамид и других многоугольников
Как и в примере с кубом выше, любая трехмерная фигура может иметь несколько цепей, а не одну, но вот несколько трехмерных фигур с примерами только одной из их цепей.Посмотри, сможешь ли ты еще немного потренироваться.
Сети изогнутых тел
Все приведенные выше примеры сконцентрированы на плоских многоугольниках. Изогнутые формы тоже могут иметь сетки. Их проще визуализировать и построить, если твердое тело имеет хотя бы одну плоскую поверхность. Вот несколько примеров.
Сфера или глобус
У сферы нет плоских поверхностей, это непрерывная кривая.
Создание плоской двумерной сети земного шара веками было проблемой для картографов (картографов).Когда мы смотрим на сетку сферы, мы можем понять, почему картографам было трудно ее использовать. Тем не менее, карты мира были произведены таким образом:
Представьте, что у вас есть апельсин, и вы разрезаете его на дольки. Когда вы съедите мясо, у вас останутся кусочки кожи. Если бы вы выстроили их в линию, то они были бы похожи на сеть из сферы.
Однако у этого подхода есть недостаток. Независимо от того, сколько сегментов, каждый из них будет иметь плоскую поверхность.
Еще раз посмотрев на ваши кусочки апельсиновой кожицы, они не только изгибаются сверху вниз, но также изгибаются из стороны в сторону, в отличие от страницы, которая может изгибаться только в одном направлении. Это называется двойной кривизной . Поэтому невозможно создать полностью точную 2D-сетку 3D-формы с двойной кривизной. Даже если бы в приведенной выше сети было 100 сегментов, это все равно было бы приблизительным значением.
Картографы в конце концов решили эту проблему, создав карты на основе цилиндра, получившего название проекции .Это тоже приближение, но оно включает искаженный вид поверхности земного шара, что позволяет точно измерять расстояния на плоской карте. Для получения дополнительной информации см. Нашу страницу о полярных, цилиндрических и сферических системах координат .
Заключение: Зачем вообще нужны сети?
Умение понимать, как трехмерная форма состоит из двухмерных компонентов, — это не только полезный навык, если вам нужно построить коробку, но также жизненно важно в любом аспекте трехмерного дизайна.
Инженеры и дизайнеры используют сложные и мощные пакеты автоматизированного проектирования (САПР), чтобы спроектировать все, от плоской мебели до крупнейших круизных лайнеров в мире.
Важные пространственные навыки, которые вы приобретаете из базового понимания фигурных сетей, могут поэтому развиваться в других, более сложных конструкторских приложениях.
Дополнительные материалы по навыкам, которые вам нужны
Понимание геометрии
Часть необходимых навыков Руководство по счету
Эта электронная книга охватывает основы геометрии и рассматривает свойства форм, линий и твердых тел.Эти концепции выстроены в книге с отработанными примерами и возможностями, позволяющими вам практиковать свои новые навыки.
Если вы хотите освежить в памяти основы или помочь своим детям в обучении, эта книга для вас.
Как сделать модульную коробку-кубик оригами
Как сделать модульную коробку-куб для оригами
Никто не знает, кто первым создал блок Sonobe, поэтому теперь он считается «традиционным оригами».
Есть много разных форм, которые вы можете сделать с помощью устройств Sonobe.На этот раз вы узнаете, как сделать элементы, а затем собрать из них простой куб.
Вам понадобится шесть листов квадратной бумаги. Полезно использовать два или более листов разного цвета.
Начало складок
Ель / Крисси ПкНачните с бумаги белой стороной вверх, если она есть.
- Сложите лист пополам слева направо и разверните. Теперь у вас есть центральная складка.
- Загните левый и правый края к центральной складке и разверните.
- Загните верхний левый угол и нижний правый угол внутрь, совмещая с двумя предыдущими складками.
- Загните левый и правый края обратно к центральной складке.
Сделайте диагональные складки, поверните и повторите
Ель / Крисси Пк- Согните нижнюю левую часть по диагонали вверх вправо вдоль диагонального клапана, который находится в правой части.
- Заправьте только что созданный лоскут под правую часть.
- Поверните бумагу и согните левый нижний угол вверх так же, как и раньше.
Подключите свои устройства Sonobe
Ель / Крисси Пк- Вставьте заслонку под нижнюю правую часть.
- Переверните модель на другую сторону слева направо.
- Загните нижний левый угол до нижней точки правого края.
- Загните самую верхнюю точку вниз и влево.
- Теперь у вас должно быть шесть таких аппаратов «Sonobe».
- Начните с того, что возьмите одну единицу так, чтобы ее крышка была сверху и снизу.Затем возьмите еще два, поместите их слева и справа от первого. Двое с обеих сторон имеют свои откидные створки вправо и влево.
Левый : Вставьте нижнюю правую точку в нижний карман центрального блока.
Правый : Вставьте верхнюю левую точку в верхний карман на центральном блоке.
Завершение матча
Ель / Крисси Пк- Теперь возьмите еще два блока Sonobe, поместите их выше и ниже центрального блока.
- Вставьте верхнюю заслонку центрального блока в правый карман вышеприведенного.
- Вставьте нижнюю заслонку центрального блока в левый карман нижнего.
- Теперь пришло время подобрать блоки, но будьте осторожны, они не все разваливаются. Сформируйте блоки в коробку, вставив откидные створки, как показано.
- Теперь, когда у вас есть коробка, вы можете достать последнюю часть и закончить кубик оригами.
Сделайте изометрический чертеж кубической конструкции, представленной ниже.
Презентация на тему: «Сделайте изометрический чертеж кубической конструкции, представленной ниже» — стенограмма презентации:
ins [data-ad-slot = «4502451947»] {display: none! important;}} @media (max-width: 800px) {# place_14> ins: not ([data-ad-slot = «4502451947»]) {display: none! important;}} @media (max-width: 800px) {# place_14 {width: 250px;}} @media (max-width: 500 пикселей) {# place_14 {width: 120px;}} ]]> 1 Сделайте изометрический чертеж кубической конструкции, представленной ниже.
Чертежи, сети и другие модели УРОК 1-2 Дополнительные примеры Быстрая проверка Сделайте изометрический чертеж кубической структуры, представленной ниже. Вы нарисуете все края фигуры, которые видите. Начните с рисования лицевой стороны фигуры. Далее прорисовываем задние края фигурки. Наконец, заполните правую грань, верхнюю грань и левый край. Шаг 1: Нарисуйте перед. Шаг 2: Отведите спинку. Шаг 3: Завершите.
2 Сделайте орфографический чертеж изометрического чертежа, представленного ниже.
Чертежи, сети и другие модели УРОК 1-2 Дополнительные примеры Сделайте орфографический чертеж изометрического чертежа, представленного ниже. Ортографические рисунки сглаживают глубину фигуры. Орфографический чертеж показывает три вида. Поскольку ни один край изометрического чертежа не скрыт на виде сверху, спереди и справа, все линии сплошные. Быстрая проверка
3 Чертежи, сети и другие модели
УРОК 1-2 Дополнительные примеры Чтобы сделать чертеж фундамента, используйте вид сверху ортогонального чертежа.Быстрая проверка
4 Чертежи, сети и другие модели
УРОК 1-2 Дополнительные примеры (продолжение) Поскольку вид сверху состоит из 3 квадратов, покажите 3 квадрата на чертеже фундамента. Найдите квадрат, который представляет самую высокую часть. Напишите цифру 2 в заднем квадрате, чтобы обозначить, что задняя часть имеет высоту 2 куба. Напишите цифру 1 в каждом из двух передних квадратов, чтобы обозначить, что каждая передняя часть имеет высоту 1 куб.Быстрая проверка
5 A и C — это задняя и передняя грани.
Рисунки, сети и другие модели УРОК 1-2 Дополнительные примеры Является ли узор сеткой для куба? Если да, назовите две буквы, которые будут на противоположных гранях. Выкройка представляет собой сетку, потому что вы можете сложить ее в виде куба. Сложите квадраты A и C вверх, чтобы сформировать переднюю и заднюю части куба. Сложите букву D вверх, чтобы получилась сторона. Сложите E, чтобы сформировать верх.Сложите букву F вниз, чтобы получилась другая сторона. После того, как сетка сложена в куб, на противоположных гранях появляются следующие пары букв: A и C — это задняя и передняя грани. B и E — нижняя и верхняя грани. D и F — правая и левая боковые грани. Быстрая проверка
6 Думайте о сторонах квадратного основания как о
Рисунках, сетях и других моделях УРОК 1-2 Дополнительные примеры Нарисуйте сетку для фигуры с квадратным основанием и четырьмя гранями равнобедренного треугольника.Обозначьте сетку ее размерами. Думайте о сторонах квадратного основания как о петлях и «разверните» фигуру по этим краям, чтобы сформировать сетку. Основание каждой из четырех граней равнобедренного треугольника является стороной квадрата. Быстрая проверка
Уроборитм доминирующего развернутого куба | Художественные галереи
В дизайне этого лоскутного одеяла использованы две концепции, которые я посещал много раз за последние тридцать лет. Я не изобретал предметы, а скорее исследовал их. Я часто противопоставлял их друг другу, используя разные средства массовой информации, чтобы лучше понять их.Хронологически первая из моего опуса «Развернутый куб»; другой — от «Уроборос». Их сочетание расширяет мой интерес к «наклонному» геометрическому анализу композиций, присущих мозаике и плетению.
«Развернутый куб»:
Кажется, есть одиннадцать форм, которые складываются в куб (не считая зеркальных отражений). Все они вписываются в соотношение трех на четыре, за исключением одного, который я называю Superior shape . Он вписывается в соотношение два на пять, и его два сегмента могут быть заключены в скобки с помощью доминирующей формы .Форма Доминант уникальна для остальных девяти форм рациона три на четыре. это непрерывная линия, начинающаяся с одной стороны куба и закручивающаяся вокруг его экватора к противоположной стороне. Две другие формы, правильная и неправильная кардинальные формы, непрерывны и связаны. Их меньшие версии были помещены в две большие формы.
«Уроборос»:
Уроборос — гностический дракон второго века, вечно кусающий себя за хвост. Иногда, как (возможно) в этом случае, он появляется как петух со змеиным хвостом, что символизирует невидимый дух, якобы пронизывающий все.С одной стороны, она самодостаточна, с другой — распущена. От самопознания к самоукрашиванию, затем от самообмана к самоуничтожению. Оба конца соединяются.
Гностики были христианскими еретиками, выступавшими против материализма католической церкви. Они считали, что Иисус был больше эпохой, чем телом. Считая довольно противоречивым для них изображать Уроборос как единое целое, я изобразил его, изобразив его части, стремящиеся к объединению. Не присваивая их часто встречаемый символ, а скорее абстрагируя его современным способом, я попытался улучшить передачу их идеи.Я сделал один рисунок более эмбриональным, чем другой, предполагая, что он существует до рождения или зачатия, во сне или стремлениях. Другой более развит, материализован или реален. Эти двое смешиваются друг с другом в ритме, пытаясь объединиться. Я наложил их, чтобы сформировать четыре переплетенных повторяющихся узора, или «гильоши», используемых для выстегивания узора развернутого куба. При удалении границы открывается целая плитка, которую можно соединить сверху и снизу или из стороны в сторону, что указывает на потенциально бесконечное поле.
Уроборитм развернутого куба предполагает случайное нарушение некоего идеала, пробуждающего жизнь.Стремление к слиянию двух рисунков Уроборос подразумевает, что наши мечты стремятся материализоваться так же, как мы стремимся осуществить свои мечты. Обсуждение этой концепции открыло во мне осознание времени / пространства взаимного влияния между прошлым, настоящим и будущим. Я подозреваю, что то, что мы делаем в настоящем, влияет на наше прошлое; и мы действуем в ответ на подсознательное знание нашей судьбы.
Эндрю Джеймс Смит, 16 мая 2003 г.
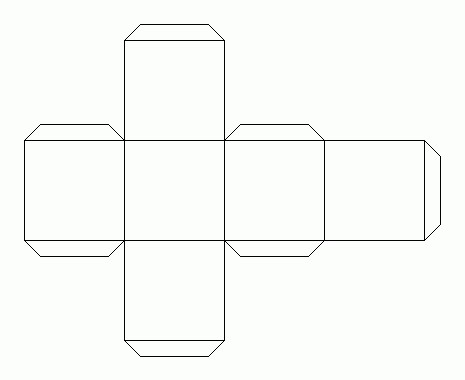
 Таких элементов у куба
8. Что это? (Вершина)
Таких элементов у куба
8. Что это? (Вершина)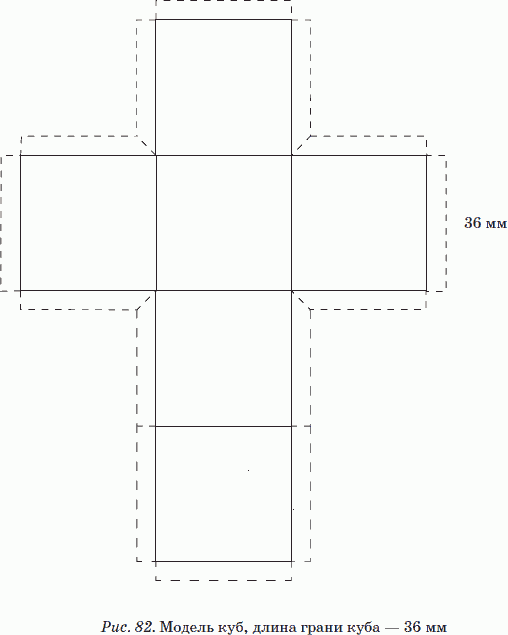 А пока, надо из подручных средств соорудить наклонную плоскость и прикрепить к ней лист бумаги.
А пока, надо из подручных средств соорудить наклонную плоскость и прикрепить к ней лист бумаги.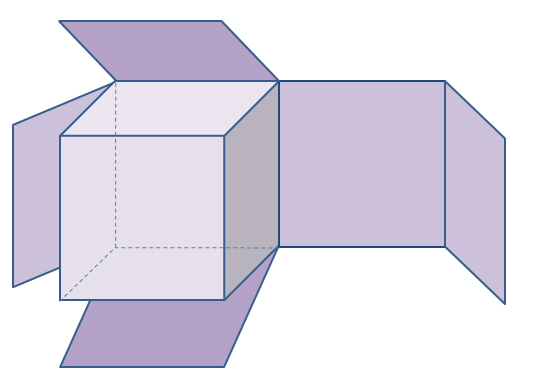 Удобно расположились на расстоянии вытянутой руки. Взяли и держим правильно карандаш, большой палец сверху, остальные под карандашом. Точка, в которой мы держим карандаш, находится, примерно, в трёх сантиметрах от острия. Отлично.
Удобно расположились на расстоянии вытянутой руки. Взяли и держим правильно карандаш, большой палец сверху, остальные под карандашом. Точка, в которой мы держим карандаш, находится, примерно, в трёх сантиметрах от острия. Отлично.
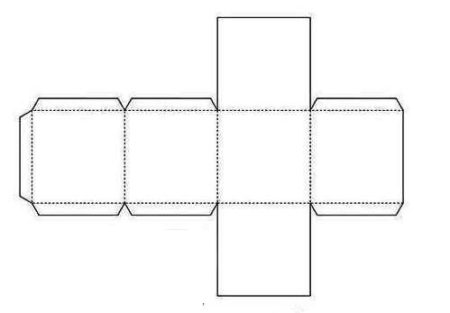 Из этой точки проведём линии – радиусы вверх, вниз, вправо, влево. Таким образом, мы разделим круг на четыре части. Не спеша, заполним такими же линиями – радиусами все четыре сектора круга. Там, где линии, покажутся вам редко расположенными, добавьте, проведя дополнительные линии от окружности к центру. Заполняйте линиями круг до тех пор, пока все линии не сольются в одно сплошное пятно. Отлично, мой друг, я поздравляю тебя с положенным началом творческого периода.
Из этой точки проведём линии – радиусы вверх, вниз, вправо, влево. Таким образом, мы разделим круг на четыре части. Не спеша, заполним такими же линиями – радиусами все четыре сектора круга. Там, где линии, покажутся вам редко расположенными, добавьте, проведя дополнительные линии от окружности к центру. Заполняйте линиями круг до тех пор, пока все линии не сольются в одно сплошное пятно. Отлично, мой друг, я поздравляю тебя с положенным началом творческого периода.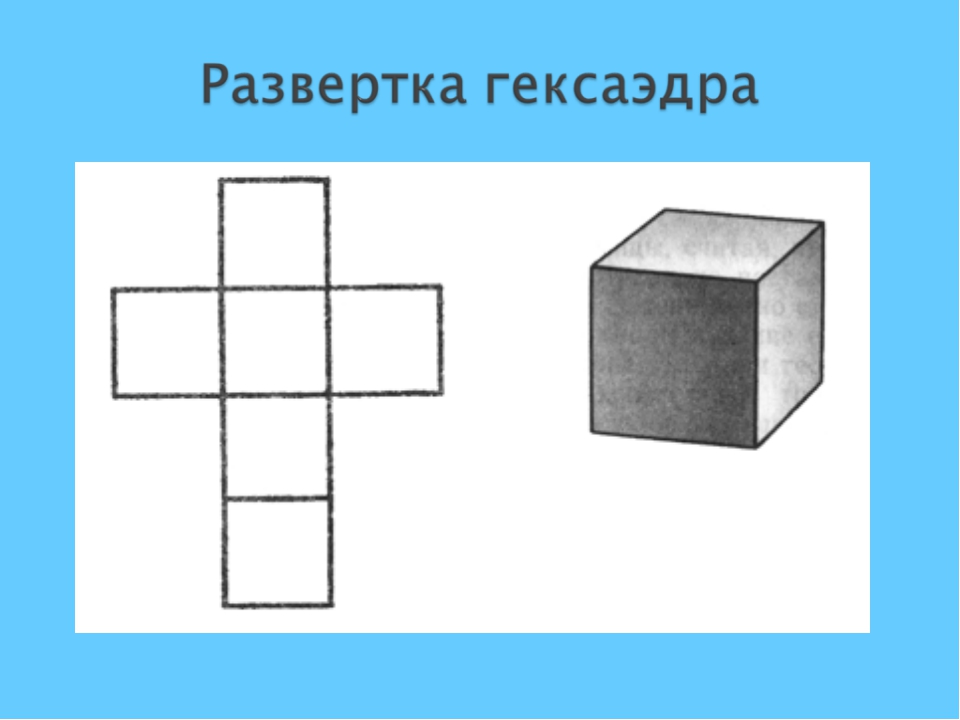
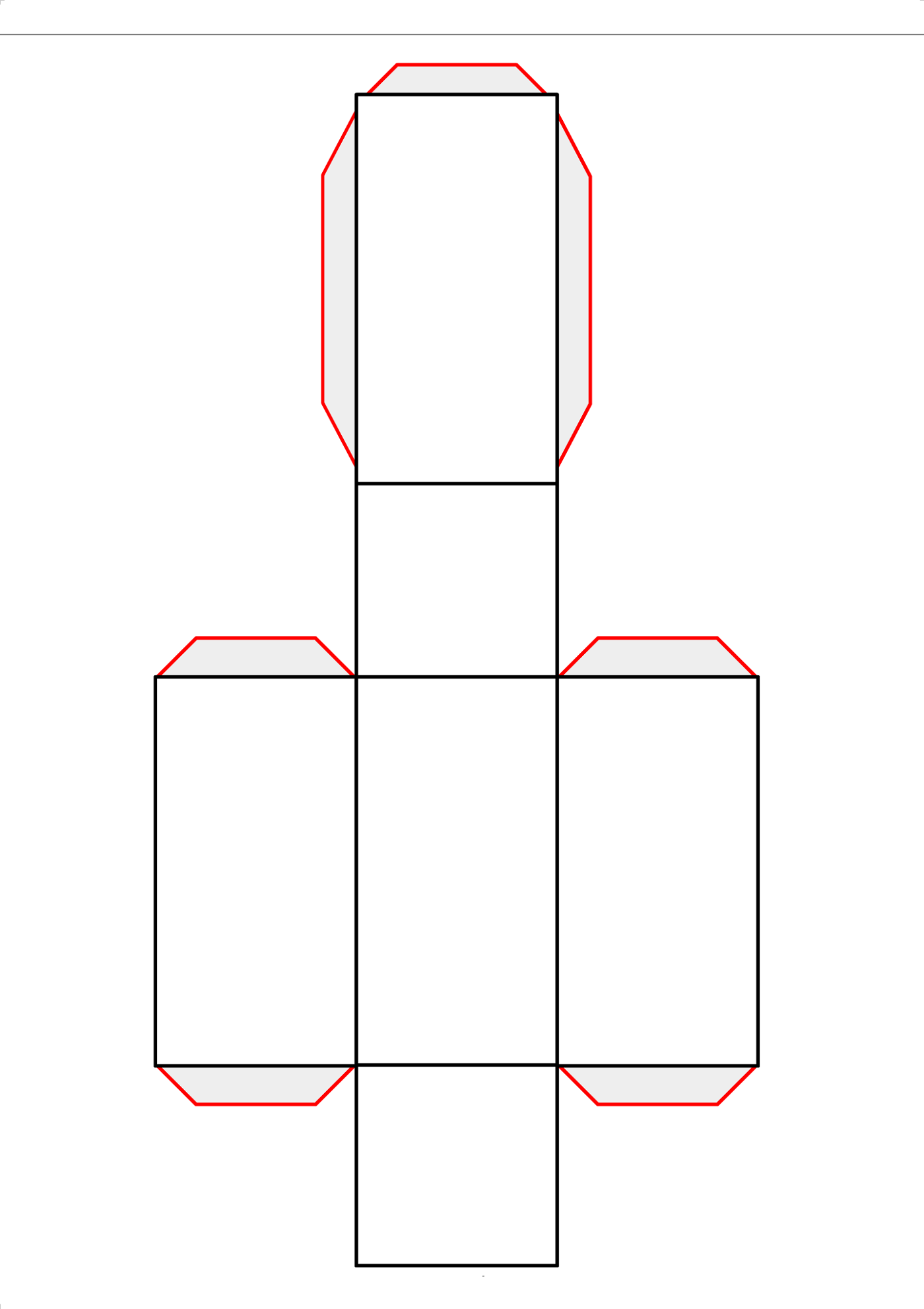 Рисуем их строго на одной линии, вплотную друг к другу.
Рисуем их строго на одной линии, вплотную друг к другу.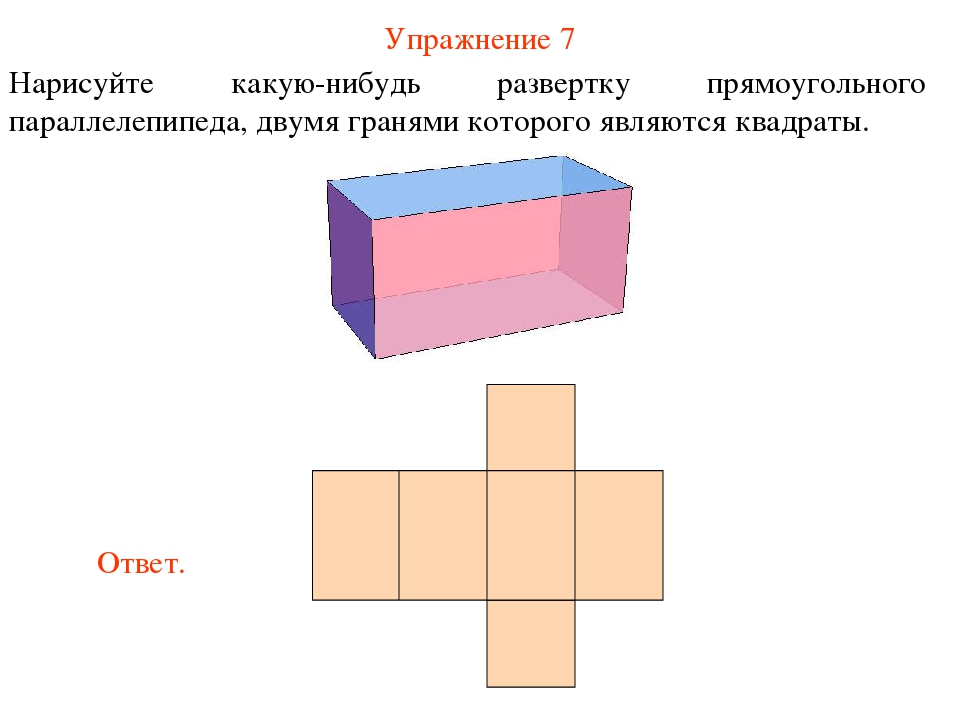 Подставив в формулу требуемый диаметр, найдем длину прямоугольника, который будем рисовать на бумаге. Дорисовываем небольшие дополнительные треугольнички, которые необходимы для склеивания деталей.
Подставив в формулу требуемый диаметр, найдем длину прямоугольника, который будем рисовать на бумаге. Дорисовываем небольшие дополнительные треугольнички, которые необходимы для склеивания деталей. Если параллелепипед не прямоугольный, то создать развертку немного сложнее. Для каждого параллелограмма нужно выдержать требуемые углы.
Если параллелепипед не прямоугольный, то создать развертку немного сложнее. Для каждого параллелограмма нужно выдержать требуемые углы.