|
Главная » Книжки-игрушки, раскраски, наклейки » Копируем фигуры по клеточкам
| ||||||||||||||||||||||||||
Как рассчитать площадь фигуры по клеточкам
Площади фигур (плоских и объемных)
Слышал ты что-нибудь про формулу Пика? Когда ее можно применять, а когда нельзя?
Сколько ты знаешь способов нахождения площади фигур на клетчатой бумаге? А их на самом деле три! И хотя задачу по нахождению площади фигур на клетчатой бумаге убрали из ЕГЭ, сам навык очень полезен для понимания планиметрии!
Во второй части мы рассмотрим как находить площади объемных фигур (призмы и пирамиды)
ПЛОЩАДИ ПЛОСКИХ ФИГУР
Способы нахождения площади фигур на клетчатой бумаге:
Способ 1.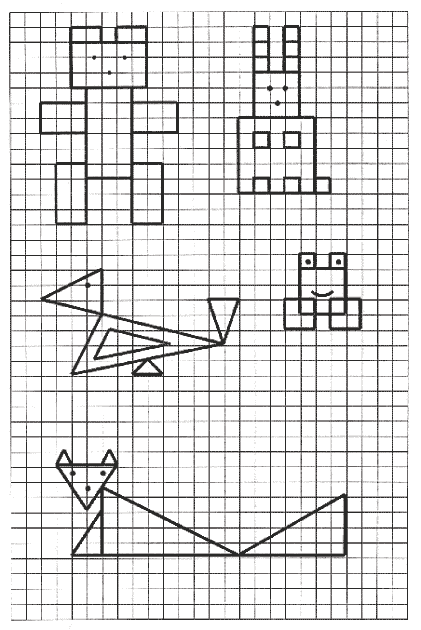 Считай клетки и применяй формулы
Считай клетки и применяй формулы
Удобен для стандартных фигур: треугольника, трапеции и т.д.
- Подсчитывая клеточки и применяя простые теоремы, найти те стороны, высоту, диагонали, которые требуются для применения формулы площади;
- Подставить найденные значения в уравнение площади.
Способ 2. Дострой до прямоугольника и вычти лишнее
Очень удобен для сложных фигур, но и для простых неплох
- Достроить искомую фигуру до прямоугольника;
- Найти площадь всех получившихся дополнительных фигур и площадь самого прямоугольника;
- Из площади прямоугольника вычесть сумму площадей всех лишних фигур.
Способ 3. Формула Пика
Работает только для многоугольников без дырок, все вершины которых попадают в узлы сетки.
- Назовём «узлами» точки пересечения линий сетки нашей клетчатой бумаги.
Подсчитаем, сколько узлов попадает в нашу фигуру. Причём, отдельно посчитаем те узлы, которые попадают внутрь нашей фигуры, и отдельно – те, которые лежат на границе.
В примере на рисунке получилось \( Г = 22\) на границе и \( В = 32\) внутри.
Формула Пика. Делим границу пополам, прибавляем внутренности и вычитаем 1:\( S = Г/2 + В – 1 \)
В примере на рисунке:
\( S = Г/2 + В – 1 = 22/2 + 32 — 1 = 42.\)
Способ 1. Считай клетки и применяй формулыУдобен для стандартных фигур: треугольника, трапеции и т.д.
- Подсчитывая клеточки и применяя простые теоремы, найти те стороны, высоту, диагонали, которые требуются для применения формулы площади;
- Подставить найденные значения в уравнение площади.
Пусть нужно найти площадь трапеции, построенной на листе в клетку.
Просто считаем клеточки и видим, что в нашем случае \( \displaystyle a=17\), \( \displaystyle b=6\) и \( \displaystyle h=6\). Подставляем в формулу:
\( \displaystyle S=\frac\cdot h=\frac\cdot 6=69\)
Но бывает, что не так-то просто рассчитать, сколько клеток в нужном отрезке. Вот смотри, треугольник:
Вот смотри, треугольник:
Вроде бы даже прямоугольный и \( \displaystyle S=\frac\cdot ab\), но чему тут равно \( \displaystyle a\), и чему равно \( \displaystyle b\)?
Найдем \( \displaystyle a\) по теореме Пифагора из \( \displaystyle \Delta ADC\), а \( \displaystyle b\) по теореме Пифагора из \( \displaystyle \Delta BCE\).
Благо на листе в клетку легко посчитать длину катетов.
Значит, \( \displaystyle a=\sqrt=2\sqrt\)
Подставляем в формулу:
\( \displaystyle S=\frac\cdot ab=\frac\cdot 2\sqrt\cdot \sqrt=13\).
Способ 2. Дострой до прямоугольника и вычти лишнееОчень удобен для сложных фигур, но и для простых неплох
- Достроить искомую фигуру до прямоугольника;
- Найти площадь всех получившихся дополнительных фигур и площадь самого прямоугольника;
- Из площади прямоугольника вычесть сумму площадей всех лишних фигур.
Давай посчитаем площадь того же треугольника вторым способом.
Нужно окружить нашу фигуру прямоугольником. Вот так:
Получился один (нужный) треугольник внутри и целых три ненужных треугольника снаружи. Но зато площади этих ненужных треугольников легко считаются на листе в клетку!
Вот мы их посчитаем, а потом просто вычтем из целого прямоугольника:
\( \displaystyle _>=\frac\cdot 6\cdot 4=12\)
\( \displaystyle _>=\frac\cdot 7\cdot 4=14\)
\( \displaystyle _>=\frac\cdot 3\cdot 2=3\)
\( \displaystyle \Rightarrow S=42-12-14-3=13\)
Почему бы просто не считать клеточки?
Возможно, вы читаете всё это и думаете: зачем все эти сложности? Формулы запоминать. Дорисовывать. Тут ведь сразу видно, сколько клеточек в фигуре.
Вот, например, трапеция:
Посчитаем клеточки: их всего 46, верно?
Но стоп, там же некоторые из них только наполовину внутри фигуры. Отметим их – всего таких 10. Итого, 36 полных (красные точки) и 10 половинчатых, вместе \( 36+\frac = 41\)
Вроде бы всё верно. Но, если присмотреться, можно заметить ещё маленькие треугольнички, которые попали внутрь. А также, что «синие» клеточки слева на самом деле разрезаны не ровно пополам – какие-то чуть больше, какие-то меньше…
Но, если присмотреться, можно заметить ещё маленькие треугольнички, которые попали внутрь. А также, что «синие» клеточки слева на самом деле разрезаны не ровно пополам – какие-то чуть больше, какие-то меньше…
Как всё это учитывать?
Попробуем рассуждать так: заметно, что тот маленький розовый треугольник дополняет серый кусок клетки.
А жёлтые сколько занимают? Постарайтесь ответить сами.
Если всё сделать правильно, то увидите, что жёлтые кусочки можно сложить вместе в одну целую клетку.
Итак, 2 жёлтых куска = 1 клетка.
Розовый треугольник + серый кусок = 1 клетка. Всего у нас две таких пары (розовый+серый) – это 2 полных клетки.
Всё остальное как было: 36 полных клеток и 6 половинок у правой стороны – это \( 36+\frac=39\) клетки.
Итого клеток: \( 1 + 2 + 39 = 42\).
Проверим результат по формуле площади трапеции: нижнее основание 11, верхнее основание 3, высота 6. Полусумма оснований равна 7, умножаем на высоту – получилось 42. Всё совпало.
Всё совпало.
Но! Настолько ли проще был наш способ подсчёта клеточек? Не сказал бы. А если там будет несколько косых линий, то вообще можно замучиться собирать этот паззл (искать, какие кусочки друг друга дополняют).
Способ 3. Формула ПикаСуществует довольно удобная формула, которая использует клеточки для вычисления площади. А то, что мы только что проделали, – очень полезное упражнение, которое поможет эту формулу понять.
Назовём «узлами» точки пересечения линий сетки нашей клетчатой бумаги.
Теперь вместо клеточек или их частей подсчитаем, сколько узлов попадает в нашу фигуру. Причём, отдельно посчитаем те узлы, которые попадают внутрь нашей фигуры, и отдельно – те, которые лежат на границе.
У меня получилось \( Г = 22\) на границе и \( В = 32\) внутри.
Ну а теперь сама формула:
Делим границу пополам, прибавляем внутренности и вычитаем 1:
Называется она формулой Пика, поскольку доказал её математик Георг Пик 120 лет назад (да, она не специально для ЕГЭ была придумана, но очень нам помогает)
Как запомнить формулу Пика
Всё, что внутри, берём целиком (клетки внутри фигуры целые).
Граница режет клетки надвое, поэтому берём половину узлов границы.
Минус 1 – это надо просто запомнить. Очень легко себя проверить на квадрате 1×1. Его площадь равна 1. Сколько там точек на границе? \( Г = 4.\) А сколько внутри? \( В = 0\) (нисколько)
Границу делим пополам, получаем 2. Прибавляем внутренности (+0) – ничего не поменялось.
Очевидно, что осталось вычесть 1, чтобы получить 1.
Проверьте эту формулу на других простых фигурах, чтобы убедиться и закрепить.
Вычислите площадь простых фигур тремя способами
Стороны клеток равны 1. Вычислите самостоятельно площадь фигуры всеми тремя способами. Сравните результаты.
Вычислите площадь произвольных фигур по формуле Пика
Вычислите самостоятельно площади фигур с помощью формулы Пика:
Посчитайте площадь корабля и котика по формуле Пика
Посчитайте самостоятельно для тренировки и чтобы запомнить формулу Пика!
Фигуры с отверстиями — посчитайте площади двумя способами
Ну и напоследок фигуры с «дырками».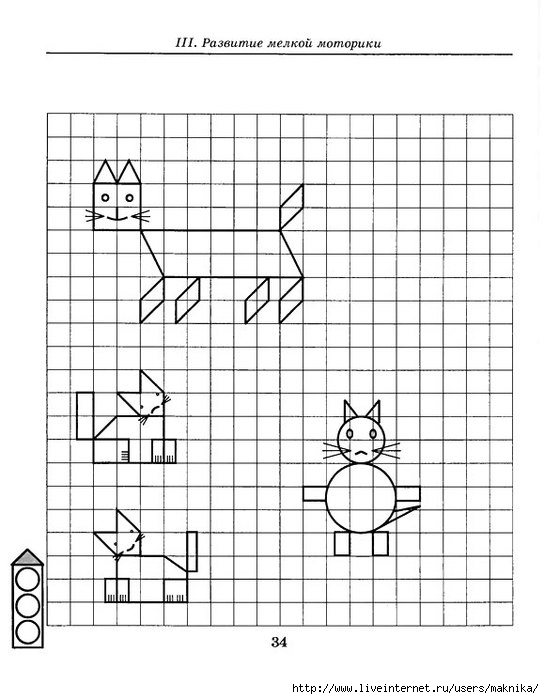 Как думаешь, здесь придётся вычислять сначала площадь целой фигуры, а потом площадь дырки?
Как думаешь, здесь придётся вычислять сначала площадь целой фигуры, а потом площадь дырки?
Или достаточно просто посчитать точки внутри закрашенной области и на её границах (в том числе, на границе с дыркой)?
Проверим на простом примере: это квадрат \( 4\times 4\), и в нём вырезан прямоугольник \( 1\times 2\), значит, его площадь \( 16-2=14\).
А теперь по точкам. На границах (включая внутренние) \( Г = 22\). Внутри \( В = 3\). Тогда площадь по формуле Пика
Хм, близко, но не совпало. Может, я где-то ошибся? Давай ещё одну фигуру, для верности.
Сосчитай сам и проверь.
У меня снова на 1 меньше.
Так может быть просто формулу немного «подкрутить»? Нет!
Очень и очень не рекомендую вам запоминать несколько похожих формул для похожих случаев, потому что придёт время, и вы обязательно перепутаете формулу.
Даже если вы уверены, что не перепутаете, оно всё равно того не стоит. В общем, наилучший вариант – это запомнить одну формулу. А если попалась фигура с дыркой, вычислить всю фигуру, а потом дырку. И вычесть.
А если попалась фигура с дыркой, вычислить всю фигуру, а потом дырку. И вычесть.
Когда формулу Пика применять нельзя?
Естественно, эта формула не работает для окружностей и любых других фигур с «кривыми» границами.
Также она не сработает, если хотя бы одна из вершин не попадает на узел, например, вот для такой, как на рисунке.
Почему я уверен, что не сработает? Ведь можно взять и не учитывать эту вершину, раз она не в узле. То есть
\( Г = 10, В = 2, S = \frac + 2 – 1 = 6.\)
А очень просто: я возьму и «отрежу» эту вершину. Тогда будет не треугольник, а трапеция, и площадь, очевидно, станет меньше на тот отрезанный кусочек.
Но по формуле она останется такой же, ведь количество узлов не изменилось ни на границе, ни внутри. То есть мы получим, что площадь уменьшенного треугольника равна площади целого, чего, конечно же, не может быть.
Итак, формула Пика работает только для многоугольников без дырок, все вершины которых попадают в узлы сетки.
Какой способ лучше?
Второй и третий способы универсальные. Они помогут посчитать площадь даже самых замысловатых фигур. Вернемся еще раз ко второму способу.
Вот смотри, нужно посчитать площадь такой фигуры:
Окружаем ее прямоугольником и снова получаем одну нужную, но сложную площадь и много ненужных, но простых.
А теперь чтобы найти площадь \( \displaystyle S\) просто находим площадь прямоугольника и вычитаем из него оставшуюся площадь фигур на клетчатой бумаге \( \displaystyle _>+_>+_>+_>\).
\( \displaystyle _>=\frac\cdot 6\cdot 4=12\)
\( \displaystyle _>=\frac\cdot a\cdot h=\frac\cdot 5\cdot 4=10\) (обрати внимание, \( \displaystyle _>\) площадь НЕ прямоугольного треугольника, но все равно легко считается по основной формуле).
\( \displaystyle _>=\frac\cdot 5\cdot 2=5\)
\( \displaystyle _>=\frac\cdot 1\cdot 11=5,5\).
Вот и ответ: \( \displaystyle S=33,5\).Ну как тебе этот способ?
Вот смотри. С одной стороны, когда фигура занимает много клеточек, их замучаешься считать и можно ошибиться.
С одной стороны, когда фигура занимает много клеточек, их замучаешься считать и можно ошибиться.
С другой стороны, когда мы дорисуем до прямоугольника, нужно считать много площадей.
Поэтому использование того или иного способа зависит лишь от конкретной задачи.
ПЛОЩАДИ ОБЪЕМНЫХ ФИГУР
Площадь поверхности призмы
Есть ли общая формула? Нет, в общем случае нет. Просто нужно искать площади боковых граней и суммировать их.
Площадь полной поверхности призмы – это сумма площадей всех граней.
Формулу можно написать для прямой призмы:
\( \displaystyle >_>=\text\cdot \text
\), где \( \displaystyle P\) — периметр основания.
Но всё-таки гораздо проще в каждом конкретном случае сложить все площади, чем запоминать дополнительные формулы. Для примера посчитаем полную поверхность правильной шестиугольной призмы.
Пусть сторона основания равна \( \displaystyle a\), а боковое ребро равно \( \displaystyle b\).
Все боковые грани – прямоугольники. Значит \( \displaystyle >_>>=6\cdot \text\).
Площадь поверхности пирамиды
Для пирамиды тоже действует общее правило:
Площадь полной поверхности пирамиды – это сумма площадей всех граней.\( \displaystyle _>=_>+_>\)
Теперь давай посчитаем площадь поверхности самых популярных пирамид.
Площадь поверхности правильной треугольной пирамиды
Пусть сторона основания равна \( \displaystyle a\), а боковое ребро равно \( \displaystyle b\). Нужно найти \( \displaystyle _>\) и \( \displaystyle _>\).
Вспомним теперь, что
\( \displaystyle _>\) — это площадь правильного треугольника \( \displaystyle ABC\).
И еще вспомним, как искать эту площадь.
Используем формулу площади:
\( \displaystyle S=\fracab\cdot \sin \gamma \).
У нас «\( \displaystyle a\)» — это \( \displaystyle a\), а «\( \displaystyle b\)» — это тоже \( \displaystyle a\), а \( \displaystyle \sin \gamma =\sin 60^\circ =\frac>\).
Теперь найдем \( \displaystyle _>\).
Пользуясь основной формулой площади и теоремой Пифагора, находим
Внимание: если у тебя правильный тетраэдр (т.е. \( \displaystyle b=a\)), то формула получается такой:
Площадь поверхности правильной четырехугольной пирамиды
Пусть сторона основания равна \( \displaystyle a\), а боковое ребро равно \( \displaystyle b\).
В основании – квадрат, и поэтому \( \displaystyle _>=>\).
Осталось найти площадь боковой грани
Площадь поверхности правильной шестиугольной пирамиды
Пусть сторона основания равна \( \displaystyle a\), а боковое ребро \( \displaystyle b\).
Как найти \( \displaystyle _>\)?
Шестиугольник \( \displaystyle ABCDEF\) состоит ровно из шести одинаковых правильных треугольников. Площадь правильного треугольника мы уже искали при подсчете площади поверхности правильной треугольной пирамиды, здесь используем найденную формулу.
Ну, и площадь боковой грани мы уже искали аж два раза
Бонус: Вебинар из нашего курса по подготовке к ЕГЭ по математике
Этот вебинар посвящен заданию №3 из ЕГЭ на нахождение площади фигур, длин отрезков и т.д на клетчатой бумаге.
И хотя эту задачу убрали из ЕГЭ в 2021 году, сам навык очень полезен для того, чтобы начать учить геометрию, для понимания планиметрии!
Ну и просто этот вебинар легкий и классный! Послушайте его и получите удовольствие!
Теорема Пика или формула для ленивых
Каждому из нас нередко приходилось считать площадь решётчатого многоугольника (изображённого, например, на клетчатой бумаге). В основном, это делают ещё по известным со школы формулам. Но в этом случае для каждой фигуры приходится помнить выражение её площади.
Не легче ли использовать одну формулу для всех многоугольников?
— Сказка? — Нет, теорема Пика!
• Названа она в честь Георга Пика (нет, не оружия или покемона), доказавшего её в 1899 году.
Формулировка звучит так:
S = В + Г / 2 − 1, где S — площадь многоугольника, В — количество целочисленных точек внутри многоугольника, а Г — количество целочисленных точек на границе многоугольника.
• Важное замечание: формула справедлива только для многоугольников, у которых вершины расположены в узлах решетки.
Например, для многоугольника на рисунке, В=7 (красные точки), Г=8 (зелёные точки), поэтому S = 7 + 8/2 — 1 = 10 квадратных единиц.
Докажем теорему Пика:
• Рассмотрим прямоугольник со сторонами, лежащими на линиях решетки. Пусть длины его сторон равны a и b. Имеем в этом случае В = (a-1)(b-1), Г = 2a+2b и, по формуле Пика, S = (a-1)(b-1)+a+b-1 = ab .
• Рассмотрим теперь прямоугольный треугольник с катетами, лежащими на осях координат. Такой треугольник получается из прямоугольника со сторонами a и b, рассмотренного в предыдущем случае, разрезанием его по диагонали. Пусть на диагонали лежат c целочисленных точек. Тогда для этого случая В = ((a-1)(b-1)-c+2)/2, Г = (2a+2b)/2+c-1 и получаем, что S = ab/2.
Такой треугольник получается из прямоугольника со сторонами a и b, рассмотренного в предыдущем случае, разрезанием его по диагонали. Пусть на диагонали лежат c целочисленных точек. Тогда для этого случая В = ((a-1)(b-1)-c+2)/2, Г = (2a+2b)/2+c-1 и получаем, что S = ab/2.
• Теперь рассмотрим произвольный треугольник. Его можно получить, отрезав от прямоугольника несколько прямоугольных треугольников (см. рисунок). Поскольку и для прямоугольника, и для прямоугольного треугольника формула Пика верна, мы получаем, что она будет справедлива и для произвольного треугольника.
• Остается сделать последний шаг: перейти от треугольников к многоугольникам. Любой многоугольник можно триангулировать, т.е. разбить на треугольники (например, диагоналями). Отсюда по индукции следует, что формула Пика верна для любого многоугольника.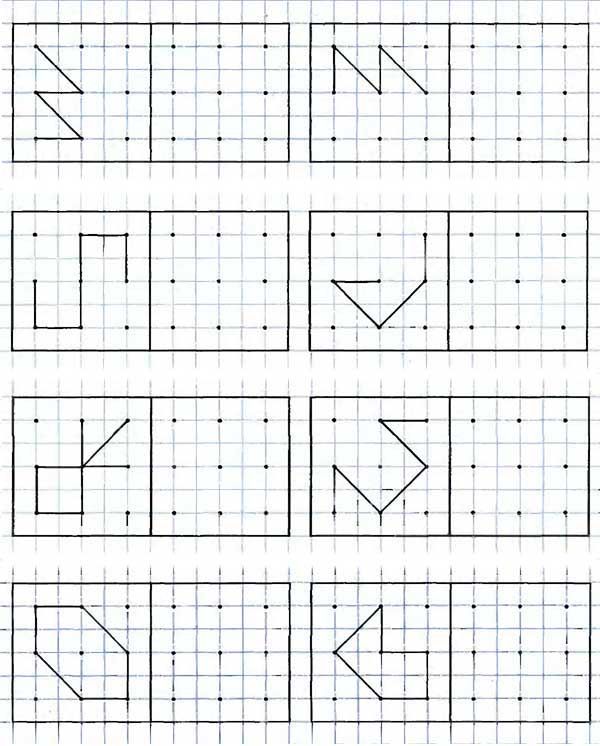 чтд
чтд
К сожалению, эта столь простая и красивая формула плохо обобщается на высшие размерности.
Наглядно показал это Рив, предложив в 1957 г. рассмотреть тетраэдр (называемый теперь тетраэдром Рива) со следующими вершинами:
A(0,0,0), B(1,0,0), C(0,1,0), D(1,1,k)
Тогда этот тетраэдр ABCD при любых k не содержит внутри ни одной точки с целочисленными координатами, а на его границе — лежат только четыре точки A, B, C, D. Таким образом, объём и площадь поверхности этого тетраэдра могут быть разными, в то время как число точек внутри и на границе — неизменны; следовательно, формула Пика не допускает обобщений даже на трёхмерный случай.
Тем не менее, некоторое подобное обобщение на пространства большей размерности всё же имеется, — это многочлены Эрхарта, но они весьма сложны, и зависят не только от числа точек внутри и на границе фигуры.
Площади многоугольников и тающий лёд
Как найти площадь многоугольника на клетчатой бумаге? Можно подсчитать число клеток, которые полностью накрыты фигурой, и ещё как-то учесть клетки, накрытые фигурой частично, — скажем, прибавить половину от числа этих клеток. И сказать, что площадь фигуры (в клеточках) приблизительно равна полученной сумме.
А можно вместо клеток, полностью или частично накрытых многоугольником, считать узлы сетки (вершины клеток) строго внутри многоугольника или на его границе.
Действительно, вокруг каждого узла сетки можно нарисовать по единичному квадратику. И если узел лежит на границе многоугольника, то этот квадратик накрыт многоугольником только частично. А если узел лежит внутри, то обычно и квадратик накрыт многоугольником полностью. впрочем, иногда всё же не полностью — но мы и считаем площадь только приближённо.
Но чудесным образом последний рецепт всегда даёт почти правильный ответ! А именно, верна Формула Пика.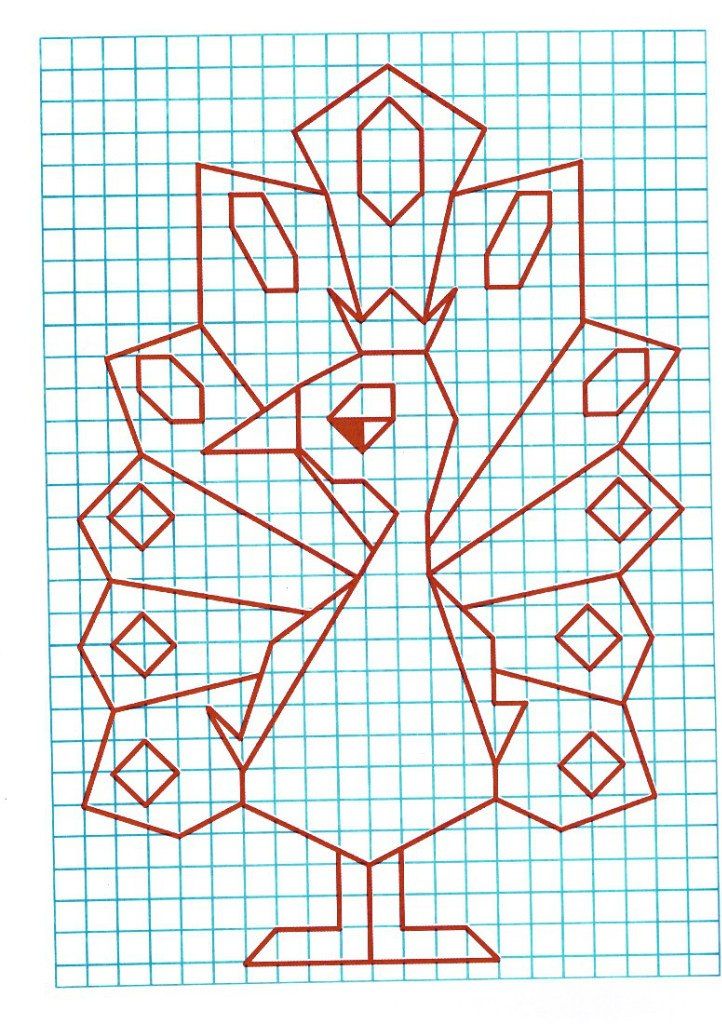 Площадь S многоугольника с вершинами в узлах сетки можно найти по формуле
Площадь S многоугольника с вершинами в узлах сетки можно найти по формуле
где i — число узлов сетки строго внутри многоугольника, b — число узлов сетки на его границе.
Подчеркнём, что это уже не приближённая, а точная формула!
Интересно, что хотя длины сторон у многоугольников обычно совершенно не целые, формула Пика гарантирует, что площадь всегда получится целой или полуцелой.
Тающий лёд
Формула Пика известна с XIX века, и с тех пор у неё появилось много доказательств, но большинство из них не такие уж простые. Мы обсудим предложенный в 1997 году швейцарским математиком Кристианом Блаттером мысленный эксперимент с тающим льдом, который сразу объясняет формулу Пика.
Поставим на каждый узел сетки по одинаковому цилиндрическому столбику изо льда. Каждый столбик очень тонкий (пересекается только с теми сторонами многоугольника, которые проходят через центр столбика) и весит 1 грамм.
Построим вокруг каждого столбика забор в виде единичного квадратика, после чего растопим весь лёд (во всех квадратиках вода растекается одинаково и симметрично относительно центра своего квадратика). Вся клетчатая плоскость будет равномерно залита водой, и в каждой ячейке площади 1 будет по 1 грамму воды. То есть количество воды в нашем многоугольнике (в граммах) будет равно его площади (в клетках).
Вся клетчатая плоскость будет равномерно залита водой, и в каждой ячейке площади 1 будет по 1 грамму воды. То есть количество воды в нашем многоугольнике (в граммах) будет равно его площади (в клетках).
С другой стороны, задумаемся, откуда эта вода попала в наш многоугольник. Посмотрим на какую-нибудь конкретную сторону многоугольника. Если через неё внутрь многоугольника втекла вода из какого-то столбика, то точно столько же воды из симметричного столбика (симметричного относительно середины этой стороны) через неё из многоугольника вытекло.
То есть внутри многоугольника ровно столько воды, сколько в нём было льда! А сколько в нём было льда? Каждый из узлов сетки внутри многоугольника даёт вклад 1 грамм, общий вес получается i граммов. Узлы на сторонах обычно дают по 1 2 грамма, но только если это не вершина, для вершины этот вес меньше — так что и общий вес узлов на границе получается не b 2 граммов, а меньше.
Насколько меньше? Продлим немного каждую сторону, обходя многоугольник вдоль сторон по часовой стрелке. На рисунке ниже красная часть дополняет каждую из синих частей до половины круга. Но красные части в сумме дают ровно один круг! Ведь, обходя многоугольник по контуру, мы в каждой вершине поворачиваемся на угол, соответствующий красной части, пока не вернёмся в исходную точку, сделав как раз полный оборот.
На рисунке ниже красная часть дополняет каждую из синих частей до половины круга. Но красные части в сумме дают ровно один круг! Ведь, обходя многоугольник по контуру, мы в каждой вершине поворачиваемся на угол, соответствующий красной части, пока не вернёмся в исходную точку, сделав как раз полный оборот.
То есть суммарный вес льда внутри многоугольника равен i + b 2 − 1 , и мы получили формулу Пика!
Упражнение
В рассуждении выше мы рисовали выпуклый многоугольник. А изменится ли что-то, если многоугольник станет невыпуклым? А если рассматривать «многоугольники с дырками»?
Геометрия. Задачи на клетчатой бумаге и площади фигур
Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы.
Это формулы площадей фигур — треугольника (5 формул), параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга. Формулы для длины окружности, длины дуги и площади сектора. Для средней линии треугольника и средней линии трапеции.
Для средней линии треугольника и средней линии трапеции.
Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения. В общем, учите основы планиметрии.
Больше полезных формул — в нашем ЕГЭ-Справочнике.
Смотри также материал: Как быстро выучить формулы
В этой статье — основные типы заданий №1 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.
Вычисление длин отрезков, величин углов и площадей фигур по формулам
1. На клетчатой бумаге с размером клетки изображена трапеция. Найдите длину средней линии этой трапеции.
Средняя линия трапеции равна полусумме её оснований:
Ответ: 3.
2. Найдите величину угла ABC. Ответ дайте в градусах.
Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна Тогда
Ответ: 45.
3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на
Решение:
Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:
Осталось умножить найденное значение синуса на
Ответ: 1.
4. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.
Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:
, где и — диагонали.
Получим:
Ответ: 12.
5. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.
Площадь трапеции равна произведению полусуммы оснований на высоту:
Основания нашей трапеции равны 4 и 8, а высота равна боковой стороне (поскольку трапеция прямоугольная), то есть 3 см. Площадь трапеции
Ответ: 18.
Нахождение площадей многоугольников сложной формы
А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ и на авторских задачах.
6. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .
Ответ: .
7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .
Видите их на рисунке? Получаем: .
Ответ: .
Многие репетиторы рекомендуют в таких задачах пользоваться формулой Пика. В ней нет необходимости, однако эта формула довольно интересна.
Согласно формуле Пика, площадь многоугольника равна В+Г/2-1
где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.
Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.
Посмотрим, как решается задача 7 с помощью формулы Пика:
Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.
Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 — 1 = 10,5.
Выбирайте — какой способ вам больше нравится.
8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки
Такой четырехугольник получится, если от квадрата размером отрезать 2 прямоугольника и 4 треугольника. Найдите их на рисунке.
Найдите их на рисунке.
Площадь каждого из больших треугольников равна
Площадь каждого из маленьких треугольников равна
Тогда площадь четырехугольника
9. Авторская задача. Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки
Решение:
На рисунке изображен ромб с вырезанным из него квадратом.
Площадь ромба равна половине произведения его диагоналей.
Площадь вырезанного квадрата равна 4.
Площадь фигуры равна 36 — 4 = 32.
Ответ: 32.
Площадь круга, длина окружности, площадь части круга
Длина дуги во столько раз меньше длины окружности, во сколько раз ее градусная мера меньше, чем полный круг, то есть 360 градусов.
Площадь сектора во столько раз меньше площади всего круга, во сколько раз его градусная мера меньше, чем полный круг, то есть 360 градусов.
10. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .
Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .
На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
Ответ: .
11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.
На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще круга, то есть круга.
Значит, нам надо умножить площадь круга на . Получим:
Ответ: 1,05.
12. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь закрашенной фигуры.
Найдите площадь закрашенной фигуры.
Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 — 9 = 7.
Ответ: 7.
Задачи на координатной плоскости
13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).
Заметим, что этот четырехугольник — квадрат. Сторона квадрата a является гипотенузой прямоугольного треугольника с катетами, равными 2 и 4. Тогда
Ответ: 20
14. Найдите площадь четырехугольника, вершины которого имеют координаты
На рисунке изображен параллелограмм (четырехугольник, имеющий две пары параллельных сторон). Площадь параллелограмма равна произведению основания на высоту. Основание равно 2, высота 8, площадь равна 16.
Основание равно 2, высота 8, площадь равна 16.
Ответ: 16.
ДИАГНОСТИЧЕСКОЕ ЗНАЧЕНИЕ ПОКАЗАТЕЛЕЙ МИТОТИКА В КЛЕТКАХ СЕРОЗНОГО ЭКСУДАТА | JAMA Internal Medicine
ДИАГНОСТИЧЕСКОЕ ЗНАЧЕНИЕ ПОКАЗАТЕЛЕЙ МИТОТИКА В КЛЕТКАХ СЕРОЗНОГО ЭКСУДАТА | JAMA Внутренняя медицина | Сеть ДЖАМА [Перейти к навигации]- Скачать PDF
- Полный текст
Поделиться
Твиттер Фейсбук Эл. адрес LinkedIn
- Процитировать это
- Разрешения
Артикул
Ноябрь 1911 г.
Л. Ф. УОРРЕН, MD
Принадлежности авторов
ANN ARBOR, MICH.
Отделение внутренних болезней Мичиганского университета.
Arch Intern Med (Шик). 1911; VIII(5):648-658. doi:10.1001/archinte.1911.00060110094009
Полный текст
Абстрактный
После сообщения Quincke 1 в 1882 г. были предприняты неоднократные попытки установить диагноз злокачественного заболевания по характеру клеток, присутствующих в плевритном или перитонеальном экссудате. Если с помощью исследовательской иглы извлекаются кусочки ткани, такой диагноз иногда может быть поставлен с достаточной степенью уверенности, как это было сделано в случае ткани, полученной в промывных водах желудка, моче, фекалиях и т. д. изолированных раковых клеток, с другой стороны, крайне неопределенно; и в 1900 Widal and Rivaut,  В одном из описанных случаев наличие многих митотических фигур делало диагноз злокачественного новообразования почти верным, во втором случае их появление в небольшом количестве
В одном из описанных случаев наличие многих митотических фигур делало диагноз злокачественного новообразования почти верным, во втором случае их появление в небольшом количестве
Полный текст
Добавить или изменить учреждение
- Кислотная основа, электролиты, жидкости
- Лекарство от зависимости
- Аллергия и клиническая иммунология
- Анестезиология
- Антикоагулянты
- Искусство и изображения в психиатрии
- Кровотечение и переливание
- Кардиология
- Уход за тяжелобольным пациентом
- Проблемы клинической электрокардиографии
- Клиническая задача
- Поддержка принятия клинических решений
- Клинические последствия базовой нейронауки
- Клиническая фармация и фармакология
- Дополнительная и альтернативная медицина
- Заявления о консенсусе
- Коронавирус (COVID-19)
- Медицина интенсивной терапии
- Культурная компетентность
- Стоматология
- Дерматология
- Диабет и эндокринология
- Интерпретация диагностических тестов
- Разнообразие, равенство и инклюзивность
- Разработка лекарств
- Электронные медицинские карты
- Скорая помощь
- Конец жизни
- Гигиена окружающей среды
- Этика
- Пластическая хирургия лица
- Гастроэнтерология и гепатология
- Генетика и геномика
- Геномика и точное здоровье
- Гериатрия
- Глобальное здравоохранение
- Справочник по статистике и медицине
- Рекомендации
- Заболевания волос
- Модели медицинского обслуживания
- Экономика здравоохранения, страхование, оплата
- Качество медицинской помощи
- Реформа здравоохранения
- Медицинская безопасность
- Медицинские работники
- Различия в состоянии здоровья
- Несправедливость в отношении здоровья
- Информатика здравоохранения
- Политика здравоохранения
- Гематология
- История медицины
- Гуманитарные науки
- Гипертония
- Изображения в неврологии
- Наука внедрения
- Инфекционные болезни
- Инновации в оказании медицинской помощи
- JAMA Инфографика
- Право и медицина
- Ведущее изменение
- Меньше значит больше
- ЛГБТК
- Образ жизни
- Медицинский код
- Медицинские приборы и оборудование
- Медицинское образование
- Медицинское образование и обучение
- Медицинские журналы и публикации
- Меланома
- Мобильное здравоохранение и телемедицина
- Нарративная медицина
- Нефрология
- Неврология
- Неврология и психиатрия
- Примечательные примечания
- Сестринское дело
- Питание
- Питание, Ожирение, Упражнения
- Ожирение
- Акушерство и гинекология
- Гигиена труда
- Онкология
- Офтальмологические изображения
- Офтальмология
- Ортопедия
- Отоларингология
- Лекарство от боли
- Патология и лабораторная медицина
- Уход за пациентами
- Информация для пациентов
- Педиатрия
- Повышение производительности
- Показатели эффективности
- Периоперационный уход и консультации
- Фармакоэкономика
- Фармакоэпидемиология
- Фармакогенетика
- Фармация и клиническая фармакология
- Физическая медицина и реабилитация
- Физиотерапия
- Руководство врача
- Поэзия
- Здоровье населения
- Профилактическая медицина
- Профессиональное благополучие
- Профессионализм
- Психиатрия и поведенческое здоровье
- Общественное здравоохранение
- Легочная медицина
- Радиология
- Регулирующие органы
- Исследования, методы, статистика
- Реанимация
- Ревматология
- Управление рисками
- Научные открытия и будущее медицины
- Совместное принятие решений и общение
- Медицина сна
- Спортивная медицина
- Трансплантация стволовых клеток
- Хирургия
- Хирургические инновации
- Хирургический жемчуг
- Обучаемый момент
- Технологии и финансы
- Искусство JAMA
- Искусство и медицина
- Рациональное клиническое обследование
- Табак и электронные сигареты
- Токсикология
- Травмы и травмы
- Приверженность лечению
- УЗИ
- Урология
- Руководство пользователя по медицинской литературе
- Вакцинация
- Венозная тромбоэмболия
- Здоровье ветеранов
- Насилие
- Женское здоровье
- Рабочий процесс и процесс
- Уход за ранами, инфекция, лечение
Сохранить настройки
Политика конфиденциальности | Условия использования
Организация типов клеток (раздел 1, глава 8) Neuroscience Online: электронный учебник по нейронаукам | Кафедра нейробиологии и анатомии
8. 1 Введение в нейроны и глиальные клетки
1 Введение в нейроны и глиальные клетки
По оценкам, нервная система человека состоит примерно из 360 миллиардов ненейронных глиальных клеток и 90 миллиардов нервных клеток. Кроме того, существуют сотни различных типов нейронов, основанных только на морфологии. Часто нейроны, которые выглядят одинаково, имеют совершенно разные свойства. Например, они используют разные нейротрансмиттеры и реагируют на них. В этом разделе рассматриваются клеточные компоненты нервной ткани. Учащиеся должны уметь описывать нейроны и глию, их морфологические компоненты, видимые в световом и электронном микроскопе, а также некоторые фундаментальные функциональные роли, которые эти типы клеток играют в нервной системе.
8.2 Модель Нейрон
Рисунок 8.1 |
После просмотра модели нейрона выше, узнайте больше о функции каждой структуры, нажав в списке ниже.
- Клеточная сома
- Дендрит
- Начальный сегмент и холмик аксона
- Аксон
- Нервные окончания
- Нервно-мышечное соединение
8.3 Cell Soma
Щелкните идентифицированные структуры на модельном нейроне, чтобы перейти к соответствующему разделу. |
Область нейрона, содержащая ядро, известна как тело клетки , сома или перикарион (рис. 8.2). Тело клетки является метаболическим центром нейрона.
Внутренняя часть сомы состоит из цитоплазмы, геля внутри микротрабекулярной решетки, образованной микротрубочками и ассоциированными белками, которые составляют цитоскелет .
Энергопроизводящий метаболизм и синтез макромолекул, используемых клеткой для поддержания своей структуры и выполнения своих функций, являются основными видами деятельности сомы нейронов. Как описано в главе 6, он также действует как восприимчивая область для синаптических входов от других клеток. В цитоплазму нейронов встроены органеллы, общие для других клеток, nucleus , nucleolus , endoplasmic reticulum , Golgi apparatus , mitochondria , ribosomes , lysosomes , endosomes , and peroxisomes . Многие из этих клеточных включений отвечают за экспрессию генетической информации, контролирующей синтез клеточных белков, участвующих в выработке энергии, росте и замещении материалов, утраченных в результате истощения.
Как описано в главе 6, он также действует как восприимчивая область для синаптических входов от других клеток. В цитоплазму нейронов встроены органеллы, общие для других клеток, nucleus , nucleolus , endoplasmic reticulum , Golgi apparatus , mitochondria , ribosomes , lysosomes , endosomes , and peroxisomes . Многие из этих клеточных включений отвечают за экспрессию генетической информации, контролирующей синтез клеточных белков, участвующих в выработке энергии, росте и замещении материалов, утраченных в результате истощения.
Рисунок 8.2 (см. увеличенный вид) |
8.4 Дендриты
Щелкните идентифицированные структуры на модельном нейроне, чтобы перейти к соответствующему разделу. |
Мембрана нейрона функционирует как рецептивная поверхность на всем своем протяжении; однако специфические входы (называемые афферентами) от других клеток поступают в основном на поверхность тела клетки и на поверхность специализированных отростков, известных как дендриты. Дендритные отростки могут сильно разветвляться и часто покрыты выростами, известными как дендритные шипы . Шипы обеспечивают огромное увеличение площади поверхности, доступной для синаптических контактов. Дендритные отростки и отростки нейронов по существу представляют собой расширения цитоплазмы, содержащие большинство органелл, обнаруженных в теле клетки. Дендриты содержат многочисленные упорядоченные массивы микротрубочек и меньше нейрофиламентов (см. ниже). Белки, ассоциированные с микротрубочками (MAP) в дендрите, имеют более высокую молекулярную массу, чем белки, обнаруженные в аксоне. Например, МАР2. Кроме того, положительные концы микротрубочек в дендритах обращены к соме клетки. Митохондрии часто располагаются продольно. Шероховатый эндоплазматический ретикулум и рибосомы присутствуют в крупных, но не в мелких дендритах. Форма и протяженность «дендритного дерева» отдельного нейрона свидетельствует о количестве и разнообразии информации, полученной и обработанной этим нейроном. Дендритные шипы часто содержат микрофиламентов , которые являются цитоскелетными элементами , ответственными за изменения формы шипов, наблюдаемые в некоторых примерах синаптической пластичности.
ниже). Белки, ассоциированные с микротрубочками (MAP) в дендрите, имеют более высокую молекулярную массу, чем белки, обнаруженные в аксоне. Например, МАР2. Кроме того, положительные концы микротрубочек в дендритах обращены к соме клетки. Митохондрии часто располагаются продольно. Шероховатый эндоплазматический ретикулум и рибосомы присутствуют в крупных, но не в мелких дендритах. Форма и протяженность «дендритного дерева» отдельного нейрона свидетельствует о количестве и разнообразии информации, полученной и обработанной этим нейроном. Дендритные шипы часто содержат микрофиламентов , которые являются цитоскелетными элементами , ответственными за изменения формы шипов, наблюдаемые в некоторых примерах синаптической пластичности.
Рисунок 8.3 (см. увеличенное изображение) |
- Просмотр препарата дендрита с шипиками под световым микроскопом
- Просмотр слайда ЭМ дендрита и позвоночника
Информация поступает в дендрит через множество рецепторов на поверхности дендрита, которые реагируют на медиаторы, высвобождаемые из окончаний аксонов других нейронов. Дендриты могут состоять из одного похожего на веточку отростка сомы или разветвленной сети, способной получать входные данные от тысяч других клеток. Например, средний спинальный мотонейрон с дендритным деревом среднего размера получает 10 000 контактов, из них 2 000 на соме и 8 000 на дендритах.
8.5 Начальный сегмент и холмик аксона
Щелкните идентифицированные структуры на модельном нейроне, чтобы перейти к соответствующему разделу. |
Конусообразная область тела клетки, где берет начало аксон, называется аксоном холмиком . Эта область свободна от рибосом и большинства других клеточных органелл, за исключением элементов цитоскелета и органелл, которые транспортируются вниз по аксону. нейрофиламенты в аксонном бугорке собираются вместе в пучки. Область между аксонным холмиком и началом миелиновой оболочки известна как начальный сегмент . Во многих случаях эта область является анатомическим местом возникновения потенциала действия. Область под аксолеммой в этой области имеет материал, который темнеет при просмотре с помощью ЭМ. Эта область показана на рисунке 8.4. На самом дистальном конце аксона и его коллатералях находятся небольшие ответвления, кончики которых представляют собой цитоплазматические расширения в форме пуговиц, называемые 9.0395 концевые бутоны или нервные окончания .
Эта область свободна от рибосом и большинства других клеточных органелл, за исключением элементов цитоскелета и органелл, которые транспортируются вниз по аксону. нейрофиламенты в аксонном бугорке собираются вместе в пучки. Область между аксонным холмиком и началом миелиновой оболочки известна как начальный сегмент . Во многих случаях эта область является анатомическим местом возникновения потенциала действия. Область под аксолеммой в этой области имеет материал, который темнеет при просмотре с помощью ЭМ. Эта область показана на рисунке 8.4. На самом дистальном конце аксона и его коллатералях находятся небольшие ответвления, кончики которых представляют собой цитоплазматические расширения в форме пуговиц, называемые 9.0395 концевые бутоны или нервные окончания .
Рисунок 8.4 (см. увеличенное изображение) |
- Вид светомикроскопического препарата аксонного бугорка сенсорного нейрона
- Просмотр слайда ЭМ аксонного холмика
8.6 Аксон
Щелкните идентифицированные структуры на модельном нейроне, чтобы перейти к соответствующему разделу. |
Другой тип процесса в идеализированном нейроне — это аксон. Каждый нейрон имеет только один аксон, и он обычно более прямой и гладкий, чем профили дендритов. Аксоны также содержат пучки микротрубочек и нейрофиламентов и разбросанных митохондрий . Большинство MAP в аксоне имеют меньшую молекулярную массу, чем в дендрите. Преобладающим MAP в аксонах является тау . Микрофиламенты внутри аксона обычно связаны с областью, прилегающей к плазмалемме, и часто являются наиболее плотными в узлах Ранвье . За пределами начальных сегментов в аксоплазме отсутствуют шероховатый эндоплазматический ретикулум и свободные рибосомы. Ветви аксонов известны как коллатеральных аксонов . Сам аксон часто окружен мембранным материалом, называемым миелиновой оболочкой, образованной клетками глии. Миелиновая оболочка изолирует плазмалемму аксона таким образом, что необходимо более быстрое распространение деполяризации плазмалемма и увеличивает скорость проведения нервного импульса (см. главу 3).
За пределами начальных сегментов в аксоплазме отсутствуют шероховатый эндоплазматический ретикулум и свободные рибосомы. Ветви аксонов известны как коллатеральных аксонов . Сам аксон часто окружен мембранным материалом, называемым миелиновой оболочкой, образованной клетками глии. Миелиновая оболочка изолирует плазмалемму аксона таким образом, что необходимо более быстрое распространение деполяризации плазмалемма и увеличивает скорость проведения нервного импульса (см. главу 3).
Рисунок 8.5 (см. увеличенное изображение) |
8.7 Нервное окончание
Щелкните идентифицированные структуры на модельном нейроне, чтобы перейти к соответствующему разделу. |
Часть плазматической мембраны нервного окончания, специализированная для образования функциональных контактов с другими клетками, представляет собой синапс .
Рисунок 8.6 Просмотреть ЭМ окончания нерва со сферическими везикулами. |
Когда нейроны взаимодействуют с мышечными волокнами, область функционального контакта называется нервно-мышечным соединением или моторным концевой пластинкой (глава 4). Согласно классическому определению синапса, когда нерв , оканчивающийся синапсами на дендрите или соме второго нейрона, называется либо аксодендритом , либо аксосоматическим синапсом соответственно (глава 7). Однако в центральной нервной системе обнаружены почти все возможные сочетания пре- и постсинаптических элементов. Эти различные типы синапсов обозначаются сочетанием названия структуры пресинаптического элемента с названием постсинаптической структуры. Например, когда передача информации происходит от аксона к аксону или от одного терминала к другому, задействованный синапс называется 9.0395 аксоаксонный синапс .
Например, когда передача информации происходит от аксона к аксону или от одного терминала к другому, задействованный синапс называется 9.0395 аксоаксонный синапс .
8.8 Клеточные элементы типичного нервного окончания
Области функциональных контактов между нейронами (синапсы) имеют отчетливые морфологические характеристики. Несмотря на то, что размер и форма бутона отдельных нейронов сильно различаются, синапсы можно идентифицировать по наличию следующего:
Рисунок 8.7 Просмотреть ЭМ окончания нерва с плоскими пузырьками. |
- Существует пресинаптический комплемент мембраносвязанных синаптических пузырьков. Это сферические везикулы в окончаниях возбудительных нервов, показанные на рис.
 8.6. В тормозных нейронах синаптические пузырьки часто уплощены, как показано на рис. 8.7.
8.6. В тормозных нейронах синаптические пузырьки часто уплощены, как показано на рис. 8.7. - Нервное окончание часто имеет скопления плотного материала в цитоплазме, непосредственно прилегающей к мембране на пре- и постсинаптической стороне соединения (они известны как пресинаптическая плотность или постсинаптическая плотность, соответственно). Этот плотный материал на пресинаптической стороне считается местом прикрепления везикул. Плотный материал на постсинаптической стороне представляет собой участок, где преобладают рецепторные белки и каналы.
- Присутствует много митохондрий , особенно в нервных окончаниях; и
- Имеется отчетливая синаптическая щель или межклеточное пространство примерно 20-40 нм.
- Присутствует эндоплазматический ретикулум , который регулирует уровень Ca 2+ .
- Эндосомальная мембрана , которая участвует в рециркуляции синаптических пузырьков.

8.9 Варианты конструкции
Существует множество вариаций «модельного» нейрона, описанного выше. Важная модификация, которая происходит особенно в рецепторных нейронах, включает обозначение нейронного отростка как дендрита или как аксона. Классически аксон был идентифицирован как миелинизированный или немиелинизированный отросток, передающий сигналы от тела клетки. Классический взгляд на дендрит — это немиелинизированная трубка цитоплазмы, которая несет информацию к телу клетки. Однако это различие справедливо не для ВСЕХ нейронов. Некоторые клетки имеют миелиновый отросток, который передает сигналы к телу клетки. Таким образом, морфологически «дендрит» и «аксон» могут быть неразличимы. Ни положение тела клетки, ни наличие или отсутствие миелина не всегда являются полезным критерием для понимания ориентации нейрона. область инициации импульса является более надежным ориентиром для понимания функционального фокуса клетки. Эта область аналогична начальному сегменту модельного нейрона, рассмотренному выше. Обычно волокно или отросток, который содержит начальный сегмент или триггерную зону, называют аксоном. Обратите внимание, как показано на рис. 8.8, триггерная зона не обязательно должна быть непосредственно примыкающей к телу ячейки.
Эта область аналогична начальному сегменту модельного нейрона, рассмотренному выше. Обычно волокно или отросток, который содержит начальный сегмент или триггерную зону, называют аксоном. Обратите внимание, как показано на рис. 8.8, триггерная зона не обязательно должна быть непосредственно примыкающей к телу ячейки.
Рисунок 8.8 |
8.10 Именование нейронов
Для классификации и именования нейронов возник ряд соглашений. Один из старейших, разработанный Гольджи в конце 1800-х годов, основан на сложности дендритного дерева нейрона. С помощью этого подхода клетки классифицируются как униполярные, биполярные и мультиполярные нейроны, как показано на рис. 8.8. Монополярные клетки имеют только один клеточный отросток и в основном встречаются у беспозвоночных. Однако сенсорные нейроны позвоночных представляют собой другую форму клеток этого типа. Поскольку эти клетки начинаются в процессе развития как биполярные нейроны, а затем по мере созревания становятся униполярными, их называют псевдоуниполярными клетками . Биполярные клетки присутствуют в сетчатке и обонятельной луковице . Мультиполярные клетки составляют остальные типы нейронов и, следовательно, являются наиболее многочисленным типом. Они были далее подразделены на клетки Гольджи II типа , которые представляют собой небольшие нейроны, обычно интернейроны, и клетки Гольджи I типа , которые представляют собой крупные мультиполярные нейроны.
Поскольку эти клетки начинаются в процессе развития как биполярные нейроны, а затем по мере созревания становятся униполярными, их называют псевдоуниполярными клетками . Биполярные клетки присутствуют в сетчатке и обонятельной луковице . Мультиполярные клетки составляют остальные типы нейронов и, следовательно, являются наиболее многочисленным типом. Они были далее подразделены на клетки Гольджи II типа , которые представляют собой небольшие нейроны, обычно интернейроны, и клетки Гольджи I типа , которые представляют собой крупные мультиполярные нейроны.
Клетки также названы по их форме (например, пирамидальные клетки , показанные на рис. 8.9) или по имени человека, впервые описавшего их (например, клетки Пуркинье , показанные на рис. 8.10). Совсем недавно клетки были названы в честь их функции или нейротрансмиттера, который они содержат (например, группы норадреналиновых клеток ЦНС, описанные в главе 12). Это описание возможно из-за развития гистохимический и иммуноцитохимический методы для специфической идентификации нейротрансмиттера типа , используемого нейронами.
Это описание возможно из-за развития гистохимический и иммуноцитохимический методы для специфической идентификации нейротрансмиттера типа , используемого нейронами.
Рисунок 8.9 | Рисунок 8.10 | |
Два варианта клеточной морфологии. Слева находится пирамидальная клетка, названная в честь ее характерной формы пирамиды. Эта клетка занимает видное место в коре головного мозга. Справа — сома клетки и дендриты клетки Пуркинье, обнаруженные в мозжечке и названные в честь ученого Пуркинье. | ||
- Рассмотрите окрашенную форму пирамидальной клетки, чтобы показать ее особенности
- Посмотреть форму окрашенной клетки Пуркинье, чтобы показать ее особенности
8. 11 Органеллы
11 Органеллы
Многие термины, используемые в этом разделе, имеют определения ниже.
Аксолемма представляет собой плазмалемму аксона.
Эндоплазматический ретикулум представляет собой лабиринтный, ограниченный мембраной компартмент в цитоплазме, где синтезируются липиды и образуются связанные с мембраной белки. В некоторых участках нейрона ЭПР лишен рибосом и называется гладким ЭПР. Гладкий ЭР участвует в Ca 2+ буферизация и биосинтез и рециркуляция синаптических везикул, как будет обсуждаться в главе 10.
Эндосома представляет собой ограниченную мембраной органеллу, которая переносит материалы, поглощенные эндоцитозом, и передает их лизосомам и пероксисомам для деградации. Он также функционирует в нервных окончаниях, рециркулируя синаптические пузырьки.
Аппарат Гольджи представляет собой совокупность уложенных друг на друга органелл с гладкой поверхностью, связанных мембраной, где белки и липиды, образующиеся в эндоплазматическом ретикулуме, модифицируются и сортируются.
Лизосомы содержат ферменты, расщепляющие соединения, образующиеся внутри или вне клеток. Они участвуют в преобразовании белков в аминокислоты и гликогена в глюкозу, основное питательное вещество нейронов. Их ферменты действуют при кислом рН. Как будет описано позже, они также служат везикулами для обратного транспорта от окончаний аксонов к соме. Многие лизосомы деградируют до гранул липофусцина, которые накапливаются по мере старения организма и считаются отходами нейронов. Лизосомы образуются в результате отпочкования аппарата Гольджи. Они имеют различные формы и размеры, связанные с мембраной, от 250 до 700 нм в диаметре.
Микрофиламенты представляют собой нити диаметром 7 нм, расположенные в виде парной спирали из двух нитей глобулярного актина. Микрофиламенты особенно заметны в синаптических окончаниях, дендритных шипиках и в ассоциации с аксолеммой.
Микротрубочки представляют собой трубчатые структуры диаметром от 20 до 25 нм, которые располагаются рыхлыми пучками вокруг ядра и направляются в основание аксональных и дендритных отростков, где они образуют параллельные массивы, распределенные в продольном направлении. Они состоят из димеров субъединиц α и β тубулина и содержат ассоциированные белки, известные как белки, ассоциированные с микротрубочками (MAPS). MAPS регулирует полимеризацию субъединиц тубулина с образованием микротрубочек. Димеры α- и β-субъединиц тубулина полимеризуются с образованием протофиламентов, расположенных в виде а-спирали, так что 13 димерных субъединиц составляют каждый полный виток а-спирали. Кроме того, микротрубочки не являются непрерывными, и каждая микротрубочка состоит из множества единиц размером 100 нм. Микротрубочки участвуют в аксоплазматическом транспорте (см. ниже).
Они состоят из димеров субъединиц α и β тубулина и содержат ассоциированные белки, известные как белки, ассоциированные с микротрубочками (MAPS). MAPS регулирует полимеризацию субъединиц тубулина с образованием микротрубочек. Димеры α- и β-субъединиц тубулина полимеризуются с образованием протофиламентов, расположенных в виде а-спирали, так что 13 димерных субъединиц составляют каждый полный виток а-спирали. Кроме того, микротрубочки не являются непрерывными, и каждая микротрубочка состоит из множества единиц размером 100 нм. Микротрубочки участвуют в аксоплазматическом транспорте (см. ниже).
Митохондрии распространены повсеместно в цитоплазме всей нервной клетки и особенно многочисленны в пресинаптических специализациях.
Нейрофиламенты представляют собой разновидность промежуточных филаментов, встречающихся в нервных клетках. Нейрофиламенты участвуют в поддержании формы нейрона и механической прочности. Хотя нейрональные нейрофиламенты классифицируются как промежуточные филаменты, их состав в нейронах отличается от состава других клеток. Они состоят из трех субъединиц, образующих трубочку диаметром 10 нм. Это нейрофиламент, который окрашивается тяжелым металлом, что позволяет визуализировать форму нейронов. Нейрофиламенты располагаются рыхлыми пучками вокруг клеточного ядра и других органелл и направляются к основанию аксональных и дендритных отростков, где образуют параллельные массивы, распределенные в продольном направлении. Нейрофиламенты более многочисленны, чем микротрубочки в аксонах, тогда как микротрубочки более многочисленны, чем нейрофиламенты в дендритах. Именно нейрофиламенты претерпевают изменения при болезни Альцгеймера, образуя нейрофибриллярные клубки.
Они состоят из трех субъединиц, образующих трубочку диаметром 10 нм. Это нейрофиламент, который окрашивается тяжелым металлом, что позволяет визуализировать форму нейронов. Нейрофиламенты располагаются рыхлыми пучками вокруг клеточного ядра и других органелл и направляются к основанию аксональных и дендритных отростков, где образуют параллельные массивы, распределенные в продольном направлении. Нейрофиламенты более многочисленны, чем микротрубочки в аксонах, тогда как микротрубочки более многочисленны, чем нейрофиламенты в дендритах. Именно нейрофиламенты претерпевают изменения при болезни Альцгеймера, образуя нейрофибриллярные клубки.
Ядрышко находится в центре ядер всех нейронов. Это заметное, глубоко окрашенное сферическое включение размером примерно в одну треть ядра. Ядрышко синтезирует рибосомную РНК, играющую главную роль в синтезе белка.
Ядро нейрона большое и круглое, обычно расположено в центре. В некоторых клетках в ядре видны массы глубоко окрашивающегося хроматина. Ядерная оболочка нейронов, как и у других клеток, представляет собой двойную мембрану, усеянную порами (ядерными порами), участвующими в ядерно-цитоплазматических взаимодействиях. Ядро в нейронах имеет сферическую форму и колеблется в диаметре от 3 до 18 микрометров в зависимости от размера нейрона. Нейроны с длинными аксонами имеют более крупное тело клетки и ядро. Как и в других клетках, основным компонентом ядра является дезоксирибонуклеиновая кислота (ДНК), вещество хромосом и генов.
Ядерная оболочка нейронов, как и у других клеток, представляет собой двойную мембрану, усеянную порами (ядерными порами), участвующими в ядерно-цитоплазматических взаимодействиях. Ядро в нейронах имеет сферическую форму и колеблется в диаметре от 3 до 18 микрометров в зависимости от размера нейрона. Нейроны с длинными аксонами имеют более крупное тело клетки и ядро. Как и в других клетках, основным компонентом ядра является дезоксирибонуклеиновая кислота (ДНК), вещество хромосом и генов.
Пероксисомы представляют собой небольшие ограниченные мембраной органеллы, которые используют молекулярный кислород для окисления органических молекул. Они содержат некоторые ферменты, которые либо производят, либо разлагают перекись водорода.
Плазмалемма нейрона выглядит в электронном микроскопе как типичная двухслойная клеточная мембрана толщиной примерно 10 нм.
Постсинаптическая плотность представляет собой окрашенное в темный цвет вещество постсинаптической клетки, прилегающей к синапсу.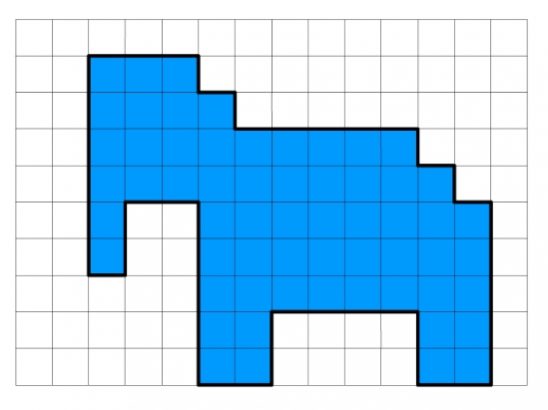 Рецепторы, ионные каналы и другие сигнальные молекулы, вероятно, связаны с этим материалом.
Рецепторы, ионные каналы и другие сигнальные молекулы, вероятно, связаны с этим материалом.
Пресинаптическая плотность представляет собой область темноокрашенного материала пресинаптической мембраны, где, как предполагается, синаптические пузырьки стыкуются перед слиянием с пресинаптической мембраной.
Рибосомы представляют собой частицы, состоящие из рибосомной РНК и рибосомного белка, которые связываются с мРНК и катализируют синтез белков. Когда рибосомы прикреплены к наружным мембранам ЭР, органелла называется шероховатым ЭР. Шероховатый ЭР в пластинках с вкраплениями рибосом виден в световой микроскоп как вещество Ниссля. В световых микроскопических препаратах вид вещества Ниссля различается в разных типах нейронов. Он может проявляться в виде густо окрашенных овоидов, мелкодисперсных частиц или скоплений гранул.
Синапс — это соединение, которое позволяет сигналам проходить от нервной клетки к другой клетке или от одной нервной клетки к мышечной клетке. Синаптическая щель представляет собой щель между мембраной пре- и постсинаптической клетки.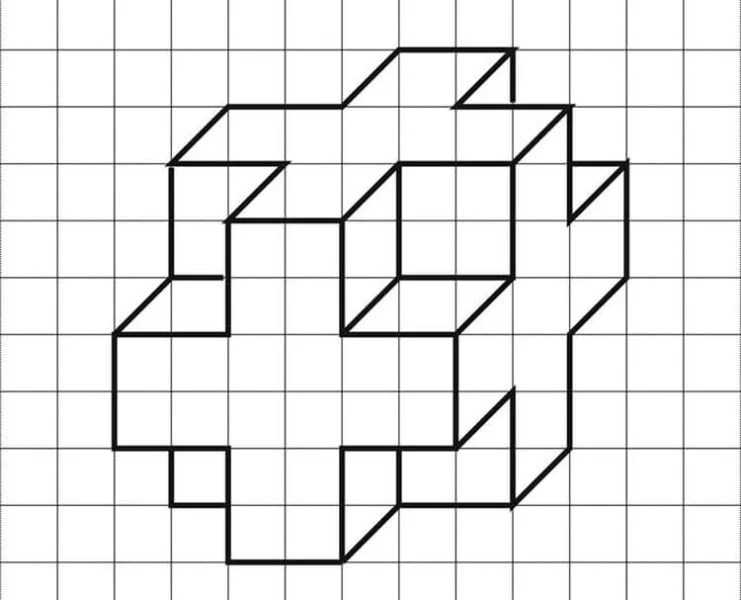 В химическом синапсе сигнал переносится диффундирующим нейротрансмиттером. Щель между пресинаптической клеткой и постсинаптической клеткой имеет ширину от 20 до 40 нм и может быть четкой или исчерченной. Недавние исследования показали, что расщелина сама по себе не является пустым пространством, а заполнена углеводсодержащим материалом.
В химическом синапсе сигнал переносится диффундирующим нейротрансмиттером. Щель между пресинаптической клеткой и постсинаптической клеткой имеет ширину от 20 до 40 нм и может быть четкой или исчерченной. Недавние исследования показали, что расщелина сама по себе не является пустым пространством, а заполнена углеводсодержащим материалом.
Синаптические везикулы представляют собой небольшие сферические органеллы в цитоплазме нейронов, содержащие нейротрансмиттер и различные белки, необходимые для секреции нейромедиатора. Везикулы, содержащие тормозной нейротрансмиттер, часто имеют плоскую или эллиптическую форму, тогда как везикулы, содержащие возбуждающий нейромедиатор, обычно имеют более сферическую форму.
8.12 Глиальные клетки и их функция
Рисунок 8.11 |
Наиболее многочисленными клеточными составляющими центральной нервной системы являются ненейрональные нейроглиальные («нервный клей») клетки, занимающие пространство между нейронами. Было подсчитано, что существует примерно 360 миллиардов глиальных клеток, которые составляют 80-90% клеток ЦНС. В этом разделе будут рассмотрены общие классификации нейроглиальных клеток и описаны некоторые общие свойства, отличающие нейроглию от нейронов.
Было подсчитано, что существует примерно 360 миллиардов глиальных клеток, которые составляют 80-90% клеток ЦНС. В этом разделе будут рассмотрены общие классификации нейроглиальных клеток и описаны некоторые общие свойства, отличающие нейроглию от нейронов.
Нейроглия отличается от нейронов несколькими общими чертами тем, что они
- не образуют синапсов,
- имеют по существу только один тип процесса,
- сохраняют способность делиться, а
- менее электрически возбудимы, чем нейроны.
Нейроглия классифицируется по размеру и форме ядра и отличается от нейронов на световом микроскопическом уровне. Щелочные (основные) красители используются для демонстрации ядерной морфологии. Кроме того, несколько металлических пятен показывают форму клетки и цитоплазматическую архитектуру. Характеристики ядер, включая размер, форму, интенсивность окрашивания и распределение хроматина, используются для различения типов клеток в патологическом материале. Также используются характеристики клеточного тела, включая размер, форму, расположение, характер ветвления и плотность отростков.
Также используются характеристики клеточного тела, включая размер, форму, расположение, характер ветвления и плотность отростков.
Нейроглия делится на две основные категории в зависимости от размера: макроглия и микроглия. Макроглия имеет эктодермальное происхождение и состоит из астроцитов , олигодендроцитов и эпендимальных клеток . Клетки микроглии , вероятно, имеют мезодермальное происхождение. Сравнение различных типов нейроглии показано на рис. 8.11.
8.13 Макроглия
Нажмите на глиальную клетку, чтобы перейти к соответствующему разделу. |
Существует три типа макроглии: олигодендроглия, эпендима и астроциты. В этом разделе обсуждаются два типа астроцитов: протоплазматические и фиброзные.
8.14 Протоплазматические астроциты
Рис. 8.12
Протоплазматический астроцит.
Протоплазматические астроциты обнаруживаются преимущественно в сером веществе. При серебряном или глиальном окрашивании их клеточные тела и отростки очень нерегулярны. Отростки могут быть большими или очень мелкими, иногда образуя листы, которые проходят между аксонами и дендритами и могут даже окружать синапсы. Эти тонкие пластинчатые отростки придают телу протоплазматической клетки астроцита «нечеткий» или мутный вид под световым микроскопом. В цитоплазме можно увидеть пучки тонких фибрилл. 9Ядро 0395 протоплазматического астроцита имеет эллипсоидную или бобовидную форму с характерными вкраплениями хроматина. Между отростками протоплазматических астроцитов отмечены специфические типы межклеточных контактов. Вероятно, они опосредуют ионный обмен между клетками.
8.15 Волокнистые астроциты
Рис. 8.13 |
Волокнистые астроциты обнаруживаются в основном в белом веществе, имеют более гладкий контур клеточного тела, чем протоплазматические астроциты, что видно с помощью глиально-специфических пятен, и имеют отростки, которые имеют тенденцию выходить из клеточного тела радиально. Эти отростки более узкие и разветвляются, образуя концевые ножки на кровеносных сосудах, эпендиме и мягкой мозговой оболочке. Следовательно, отростки волокнистых астроцитов не образуют пластов и не стремятся соответствовать форме окружающих нейронов или сосудистых элементов. Основной отличительной чертой волокнистых астроцитов, как следует из названия, является обилие глиальных фибрилл, расположенных параллельными рядами в цитоплазме и простирающихся в отростки.
При окрашивании по Нисслю волокнистых астроцитов имеют ядро по существу такое же, как и у протоплазматического типа, с пятнистым внешним видом. Между волокнистыми астроцитами также наблюдались межклеточные сращения.
Между волокнистыми астроцитами также наблюдались межклеточные сращения.
Рисунок 8.14 |
Оба типа астроцитов поддерживают нейроны в непосредственной близости от них. Они обеспечивают физический барьер между клетками, поддерживают ионное и рН-равновесие внеклеточного пространства вокруг нейронов и постоянно изменяют химическую среду соседних клеток. Как показано на рис. 8.14, астроциты образуют полную выстилку вокруг внешней поверхности ЦНС ( глиальных пределов ) и вокруг кровеносных сосудов ( периваскулярных ножек 9).0396). Во время развития они образуют каркас, по которому мигрируют нервные клетки, чтобы достичь своей зрелой структуры. Во время повреждения астроциты пролиферируют и фагоцитируют мертвых клеток. Это часто приводит к образованию глиального рубца .
Это часто приводит к образованию глиального рубца .
В дополнение к этим общим функциям астроциты также действуют более специализированными способами, облегчая работу нейронов. Они метаболизируют нейротрансмиттеры, удаляя их из синаптической щели. Например, глутамат аминокислоты поглощается астроцитами и инактивируется путем превращения в глутамин. Затем глютамин транспортируется к нейрону для повторного синтеза в глутамат (см. главу 13). Более свежие данные указывают на то, что астроциты могут резко изменять размер как часть их физиологической регуляции нейронной среды. Эти функции будут обсуждаться в следующих разделах.
8.16 Олигодендроглия
Нажмите на глиальную клетку, чтобы перейти к соответствующему разделу. |
Олигодендроциты также расположены как в сером, так и в белом веществе. Они являются преобладающим типом клеток в белом веществе, где они часто располагаются в виде рядов клеток между группами нейронных отростков. Их называют межпучковая олигодендроглия и участвуют в формировании и поддержании миелина, окружающего близлежащие отростки нейронов. В сером веществе олигодендроглии обычно располагаются вблизи нейронов и поэтому известны как перинейрональные сателлитные клетки . Тела клеток олигодендроглии часто располагаются вблизи капилляров, но у них отсутствуют определенные периваскулярные концевые ножки, характерные для астроцитов.
Их называют межпучковая олигодендроглия и участвуют в формировании и поддержании миелина, окружающего близлежащие отростки нейронов. В сером веществе олигодендроглии обычно располагаются вблизи нейронов и поэтому известны как перинейрональные сателлитные клетки . Тела клеток олигодендроглии часто располагаются вблизи капилляров, но у них отсутствуют определенные периваскулярные концевые ножки, характерные для астроцитов.
Отростки олигодендроцитов меньше и более тонкие, чем у астроцитов, а форма клеточного тела от многоугольной до сферической. Олигодендроцит 9Ядро 0395 меньше ядра астроцита, расположено эксцентрично в теле клетки, содержит глыбки хроматина и может окрашиваться щелочными красителями. Цитоплазма олигодендроцитов, как правило, темнее, чем у астроцитов с серебристыми пятнами, и не содержит глиальных фибрилл (хотя они содержат микротрубочек ).
Рисунок 8.15 Посмотреть ЭМ олигодендроцитов. |
Роль олигодендроглии в центральной нервной системе, особенно межпучковых олигодендроцитов , заключается в формировании и поддержании миелина. Миелин представляет собой оболочку из мембранного материала, описанную доктором Бирном, которая обертывает аксон нейрона, как показано на рис. 8.15, для облегчения проведения потенциала действия посредством скачкообразной проводимости. Миелин состоит из концентрических слоев мембран, уплотненных друг против друга, с внутренним (т.е. против нервного волокна) и наружным воротником цитоплазмы. Как показано на рис. 8.15, один олигодендроцит способствует миелинизации нескольких соседних нервных отростков. Более того, в миелинизацию одного междоузлия аксона вносят вклад более одного олигодендроцита. Пластинки миелиновых оболочек возникают в результате спирального оборачивания аксона цитоплазматическими отростками межпучковой олигодендроглии. Кроме того, олигодендроцит, образующий особый миелин междоузлие (т. е. миелин между двумя перехватами) редко можно увидеть непосредственно рядом с покрытым миелином отростком. Это связано с тем, что тонкие цитоплазматические мостики соединяют область тела клетки олигодендроцита с внешней оболочкой миелина. Важно отметить, что область аксона, выставленная в узле Ранвье , не оголена. Это может быть место ветвления аксона, место синаптических контактов или оно может быть покрыто различными глиальными отростками. Аксон в узловой области обычно содержит скопления органелл, особенно митохондрии .
Более того, в миелинизацию одного междоузлия аксона вносят вклад более одного олигодендроцита. Пластинки миелиновых оболочек возникают в результате спирального оборачивания аксона цитоплазматическими отростками межпучковой олигодендроглии. Кроме того, олигодендроцит, образующий особый миелин междоузлие (т. е. миелин между двумя перехватами) редко можно увидеть непосредственно рядом с покрытым миелином отростком. Это связано с тем, что тонкие цитоплазматические мостики соединяют область тела клетки олигодендроцита с внешней оболочкой миелина. Важно отметить, что область аксона, выставленная в узле Ранвье , не оголена. Это может быть место ветвления аксона, место синаптических контактов или оно может быть покрыто различными глиальными отростками. Аксон в узловой области обычно содержит скопления органелл, особенно митохондрии .
В периферической нервной системе (ПНС) шванновских клеток отвечают за образование миелина. Эти клетки миелинизируют аксоны иначе, чем межпучковая олигодендроглия. Как показано на рис. 8.16, они мигрируют вокруг аксона, откладывая мембрану, покрывающую аксон, выдавливая цитоплазму шванновской клетки. Кроме того, каждое междоузлие аксона ПНС представляет собой одну шванновскую клетку. Кроме того, немиелинизированные аксоны ПНС также окружены мембранами, образованными шванновскими клетками.
Эти клетки миелинизируют аксоны иначе, чем межпучковая олигодендроглия. Как показано на рис. 8.16, они мигрируют вокруг аксона, откладывая мембрану, покрывающую аксон, выдавливая цитоплазму шванновской клетки. Кроме того, каждое междоузлие аксона ПНС представляет собой одну шванновскую клетку. Кроме того, немиелинизированные аксоны ПНС также окружены мембранами, образованными шванновскими клетками.
Рисунок 8.16 Просмотр Шванновской ячейки ЭМ. |
8.17 Эпендима
Нажмите на глиальную клетку, чтобы перейти к соответствующему разделу. |
Эпендимальные клетки происходят из раннего зародышевого эпителия , выстилающего просвет нервной трубки , и, таким образом, также являются производными эктодермы (наряду с нейронами, астроцитами и олигодендроцитами). Эпендимальные клетки выстилают желудочков головного мозга и центрального канала спинного спинного мозга . Они расположены в виде однослойного столбчатого эпителия и имеют многие гистологические характеристики простого эпителия, которые варьируются от плоского до кубического в зависимости от их расположения. Эпендима, образующая выстилку желудочка, не соединяется с базальная пластинка , но опираются непосредственно на подлежащую нервную ткань. Как показано на рис. 8.17, поверхность, обращенная к желудочку, содержит множество микроворсинок и ресничек . Эти реснички перемещают спинномозговую жидкость (ликвор ) в желудочки . Боковые границы эпендимальных клеток относительно прямые и образуют соединения с соседними клетками.
Эпендимальные клетки выстилают желудочков головного мозга и центрального канала спинного спинного мозга . Они расположены в виде однослойного столбчатого эпителия и имеют многие гистологические характеристики простого эпителия, которые варьируются от плоского до кубического в зависимости от их расположения. Эпендима, образующая выстилку желудочка, не соединяется с базальная пластинка , но опираются непосредственно на подлежащую нервную ткань. Как показано на рис. 8.17, поверхность, обращенная к желудочку, содержит множество микроворсинок и ресничек . Эти реснички перемещают спинномозговую жидкость (ликвор ) в желудочки . Боковые границы эпендимальных клеток относительно прямые и образуют соединения с соседними клетками.
Эпендимальные клетки видоизменены в различных областях желудочков в слои кубического эпителия, которые лежат на базальной мембране (образованной выростом мягкой мозговой оболочки) над богатым руслом сосудистой и соединительной ткани. это сосудистая оболочка сплетение изучалось в лаборатории, отвечающей за секрецию, поглощение и транспорт веществ в спинномозговую жидкость и из нее.
это сосудистая оболочка сплетение изучалось в лаборатории, отвечающей за секрецию, поглощение и транспорт веществ в спинномозговую жидкость и из нее.
Рисунок 8.17 Просмотр эпендимального слоя. |
8.18 Микроглия
Рис. 8.18 |
Нажмите на глиальную клетку, чтобы перейти к соответствующему разделу. |
Микроглия, в отличие от других типов глиальных клеток, происходит из эмбриональной мезодермы . Они присутствуют во всей центральной нервной системе, но, как правило, незаметны в зрелых нормальных тканях и их трудно идентифицировать с помощью светового или электронного микроскопа. Их больше в сером веществе, и они могут поражать до 5-10% нейроглии в коре головного мозга.
Их больше в сером веществе, и они могут поражать до 5-10% нейроглии в коре головного мозга.
Общий вид микроглии похож на олигодендроциты, хотя они меньше по размеру и имеют волнообразные отростки с шиповидными выступами. Ядра микроглии имеют удлиненную или треугольную форму и глубоко окрашиваются щелочными красителями.
После повреждения нервной ткани микроглия размножается и мигрирует к месту повреждения, где очищается от клеточного дебриса путем фагоцитоза . Реагирующая микроглия имеет набухшую форму с укороченными отростками и ее трудно отличить от фагоцитов с периферии или мигрирующих периваскулярные клетки . Подсчитано, что по крайней мере одна треть фагоцитов, появляющихся в области поражения, имеет происхождение из ЦНС.
Проверьте свои знания
- Вопрос 1
- А
- Б
- С
- Д
- Е
Какие из следующих типов клеток пролиферируют в ЦНС в ответ на повреждение? (Примечание: существует более одного правильного ответа. )
)
А. Нейроны
Б. Микроглия
C. Волокнистые астроциты
D. Протоплазматические астроциты
E. Макрофаги
Какие из следующих типов клеток пролиферируют в ЦНС в ответ на повреждение? (Примечание. Правильных ответов несколько.)
A. Нейроны Это НЕВЕРНЫЙ ответ.
Хотя в настоящее время это вызывает споры, большинство доказательств указывает на то, что нейроны не подвергаются клеточному делению после того, как они созрели в процессе развития организма.
Б. Микроглия
C. Волокнистые астроциты
D. Протоплазматические астроциты
E. Макрофаги
Какие из следующих типов клеток пролиферируют в ЦНС в ответ на повреждение? (Примечание. Правильных ответов несколько.)
А.
Нейроны
B. Микроглия Это ПРАВИЛЬНЫЙ ответ!
Микроглия как делится, так и мигрирует в области клеточного повреждения в центральной нервной системе в ответ на повреждение.
C. Волокнистые астроциты
D. Протоплазматические астроциты
E. Макрофаги
Какие из следующих типов клеток пролиферируют в ЦНС в ответ на повреждение? (Примечание. Правильных ответов несколько.)
А. Нейроны
Б. Микроглия
C. Волокнистые астроциты Это ПРАВИЛЬНЫЙ ответ!
Как фиброзные, так и протоплазматические астроциты подвергаются клеточному делению в ответ на повреждение.
D. Протоплазматические астроциты
E. Макрофаги
Какие из следующих типов клеток пролиферируют в ЦНС в ответ на повреждение? (Примечание. Правильных ответов несколько. )
)
А. Нейроны
Б. Микроглия
C. Волокнистые астроциты
D. Протоплазматические астроциты Это ПРАВИЛЬНЫЙ ответ!
Как фиброзные, так и протоплазматические астроциты подвергаются клеточному делению в ответ на повреждение.
E. Макрофаги
Какие из следующих типов клеток пролиферируют в ЦНС в ответ на повреждение? (Примечание. Правильных ответов несколько.)
А. Нейроны
Б. Микроглия
C. Волокнистые астроциты
D. Протоплазматические астроциты
E. Макрофаги Это ПРАВИЛЬНЫЙ ответ!
Макрофаги появляются в ЦНС после травмы и работают вместе с глиальными клетками ЦНС, фагоцитируя остатки ЦНС.
- Вопрос 2
- А
- Б
- С
- Д
- Е
Какой из перечисленных типов клеток отвечает за поддержание рН внеклеточного пространства ЦНС? (Примечание: существует более одного правильного ответа. )
)
А. Микроглия
B. Волокнистые астроциты
C. Протоплазматические астроциты
D. Эпендимальные клетки
E. Макрофаги
Какой из перечисленных типов клеток отвечает за поддержание рН внеклеточного пространства ЦНС? (Примечание. Правильных ответов несколько.)
A. Микроглия Это НЕВЕРНЫЙ ответ.
B. Волокнистые астроциты
C. Протоплазматические астроциты
D. Эпендимальные клетки
E. Макрофаги
Какой из перечисленных типов клеток отвечает за поддержание рН внеклеточного пространства ЦНС? (Примечание. Правильных ответов несколько.)
А. Микроглия
B. Волокнистые астроциты Это ПРАВИЛЬНЫЙ ответ!
C. Протоплазматические астроциты
D.
Эпендимальные клетки
E. Макрофаги
Какой из перечисленных типов клеток отвечает за поддержание рН внеклеточного пространства ЦНС? (Примечание. Правильных ответов несколько.)
А. Микроглия
B. Волокнистые астроциты
C. Протоплазматические астроциты Это ПРАВИЛЬНЫЙ ответ!
D. Эпендимальные клетки
E. Макрофаги
Какой из перечисленных типов клеток отвечает за поддержание рН внеклеточного пространства ЦНС? (Примечание. Правильных ответов несколько.)
А. Микроглия
B. Волокнистые астроциты
C. Протоплазматические астроциты
D. Эпендимальные клетки Это НЕВЕРНЫЙ ответ.
E. Макрофаги
Какой из перечисленных типов клеток отвечает за поддержание рН внеклеточного пространства ЦНС? (Примечание. Правильных ответов несколько.)
Правильных ответов несколько.)
А. Микроглия
B. Волокнистые астроциты
C. Протоплазматические астроциты
D. Эпендимальные клетки
E. Макрофаги Это НЕВЕРНЫЙ ответ.
Солнечная ячейка Рисунок € 8 | Летающий тигр Копенгаген
- Информация о продукте
Информация о продукте
Веселая солнечная лампа со светящимися глазами. Можно использовать на открытом воздухе. Меры 20 см в высоту.
- Размеры упаковки: Ш: 95 мм Д: 130 мм Д: 200 мм
- Домашняя страница
- Солнечная батарея
{{еще пятьдесят_процент_офф == правда}}
-50%
{{else product_of_the_week == true}}
Товар недели
{{еще последний_шанс == правда}}
Последний шанс
{{else limited_edition == true}}
Ограниченная серия
{{/если}}
{{если тегECO}}
Экологичные продукты
Мы классифицируем экологически чистые продукты как: изготовленные из FSC-сертифицированного древесно-бумажного материала (мин. 95%) и/или из переработанного материала (мин. 80%) и/или из возобновляемого материала (мин. 95%) и/или из легко перерабатываемых материалов (изделия из стекла, алюминия, стали или железа с содержанием > = 95%). Каждый продукт индивидуально оценивается отделом устойчивого развития. Подробнее
95%) и/или из переработанного материала (мин. 80%) и/или из возобновляемого материала (мин. 95%) и/или из легко перерабатываемых материалов (изделия из стекла, алюминия, стали или железа с содержанием > = 95%). Каждый продукт индивидуально оценивается отделом устойчивого развития. Подробнее
{{/если}} {{если изображения[1] }} {{еще}} {{/если}}
${название}
{{if compare_at_price_min > price_min}}
{{html Shopify.formatMoney(compare_at_price_min, theme.moneyFormat). replace(«,00», «»).replace(«.00», «»).replace(«zl», «zł»).replace(» кр», «кр.»»)}}
{{if price_varies}}
из
{{/если}}
{{html Shopify.formatMoney(price_min, theme.moneyFormat)}}
{{еще}}
{{если !zero_price}}
{{if price_varies}}
из
{{/если}}
{{html Shopify.
replace(«,00», «»).replace(«.00», «»).replace(«zl», «zł»).replace(» кр», «кр.»»)}}
{{if price_varies}}
из
{{/если}}
{{html Shopify.formatMoney(price_min, theme.moneyFormat)}}
{{еще}}
{{если !zero_price}}
{{if price_varies}}
из
{{/если}}
{{html Shopify. formatMoney(price_min, theme.moneyFormat).replace(«,00», «»).replace(«.00», «»).replace(«zl», «zł»).replace(» кр», «кр.»»)}}
{{/если}}
{{/если}}
formatMoney(price_min, theme.moneyFormat).replace(«,00», «»).replace(«.00», «»).replace(«zl», «zł»).replace(» кр», «кр.»»)}}
{{/если}}
{{/если}}
{{каждый вариант}}
${(downcased_option = name.toLowerCase()),»}
${( option_color_swatch = window.swatch_recently), »}
{{if option_color_swatch.indexOf(downcased_option) > -1}}
${(список цветов = »),»}
${(optionCount = 0),»}
${(количество = 0),»}
{{каждое значение}}
${(цвет = 0),»}
{{каждый вариант}}
{{если позиция == 1}}
${(цвет = варианты[($index)]. option1),»}
{{/если}}
{{если позиция == 2}}
${(цвет = варианты[($index)].option2),»}
{{/если}}
{{если позиция == 3}}
${(цвет = варианты[($index)].option3),»}
{{/если}} ${(color_2 = color.toLowerCase().replace(» «, «»)),»}
{{if colorlist.indexOf(цвет)
${цвет}
option1),»}
{{/если}}
{{если позиция == 2}}
${(цвет = варианты[($index)].option2),»}
{{/если}}
{{если позиция == 3}}
${(цвет = варианты[($index)].option3),»}
{{/если}} ${(color_2 = color.toLowerCase().replace(» «, «»)),»}
{{if colorlist.indexOf(цвет)
${цвет}
{{/если}}
${(optionCount++),»}
${(количество = optionCount / 4),»}
{{/если}} ${(colorlist = colorlist. concat(» «,color) ),»}
{{/каждый}}
{{/каждый}}
{{если количество > 4}}
concat(» «,color) ),»}
{{/каждый}}
{{/каждый}}
{{если количество > 4}}
+ ${количество — 4}
{{/если}} {{/если}} {{/каждый}}
{{каждый вариант}} ${(downcased_option = name.toLowerCase()),»} ${( option_size_swatch = ‘размер’), »} {{if option_size_swatch.indexOf(downcased_option) > -1}}
Доступны другие размеры
{{/если}} {{/каждый}}
Быстрый просмотр
{{если будет_скоро }} Вскоре {{еще}}{{если notify_me && !доступно }}
Сообщите мне, когда будет доступно
{{еще}} {{если !zero_price}}
{{если доступно}} {{другие варианты.
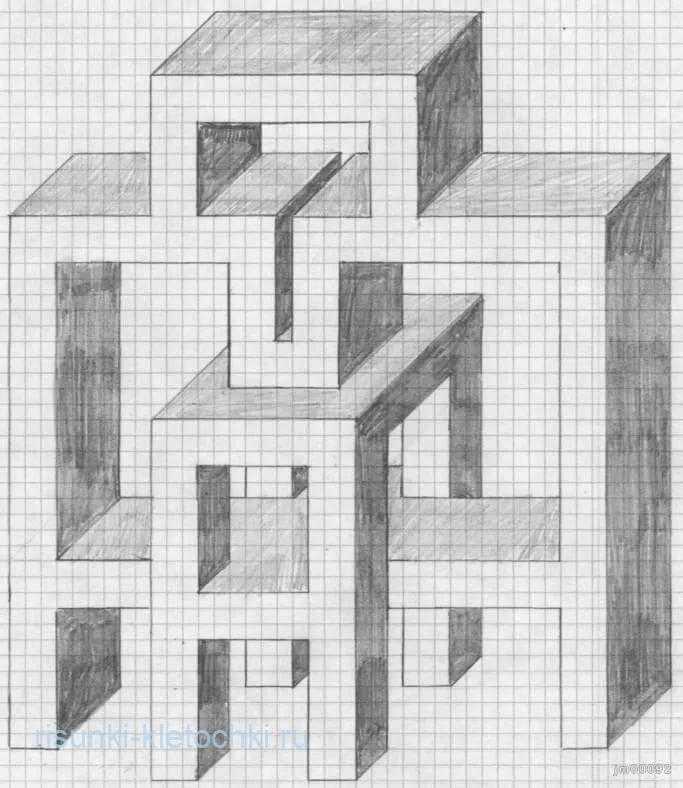
 Цель таких занятий — развитие произвольного внимания, зрительного восприятия, мелкой моторики и координации движений руки. Перед началом занятий объясните ребенку, что требуется сделать, сразу ответьте на все его вопросы, и тогда в дальнейшем малыш сможет заниматься без вашей помощи. На каждой страничке нужно сначала нарисовать картинки по клеткам в соответствии с образцом, а затем дорисовать вторую половинку фигуры по клеткам в зеркальном отражении.
Цель таких занятий — развитие произвольного внимания, зрительного восприятия, мелкой моторики и координации движений руки. Перед началом занятий объясните ребенку, что требуется сделать, сразу ответьте на все его вопросы, и тогда в дальнейшем малыш сможет заниматься без вашей помощи. На каждой страничке нужно сначала нарисовать картинки по клеткам в соответствии с образцом, а затем дорисовать вторую половинку фигуры по клеткам в зеркальном отражении.
 Наведите курсор на изображение, чтобы идентифицировать органеллы.
Наведите курсор на изображение, чтобы идентифицировать органеллы.

 8.6. В тормозных нейронах синаптические пузырьки часто уплощены, как показано на рис. 8.7.
8.6. В тормозных нейронах синаптические пузырьки часто уплощены, как показано на рис. 8.7.
 Нейроны
Нейроны Эпендимальные клетки
Эпендимальные клетки