10 Угольник вписанный в окружность – 4apple – взгляд на Apple глазами Гика
Десятиугольник, вписанный в окружность
Проводим два взаимно перпендикулярных диаметра АВ и CD. Делим пополам радиус АО в точке Е. Из Е радиусом ЕС проводим дугу CF, пересекая ею диаметр АВ в точке F. OF есть сторона искомой фигуры. С помощью циркуля, сделаем на окружности десять последовательных засечек. Получим вершины искомой фигуры. Подобно построению пятиугольника, вписанного в окружность.
Десятиугольник, описанный около окружности
Имеем исходную окружность с центром в точке O. Так как сумма углов, составляющих центральный угол окружности, равна 360°. Делим данный угол на 10 частей (т.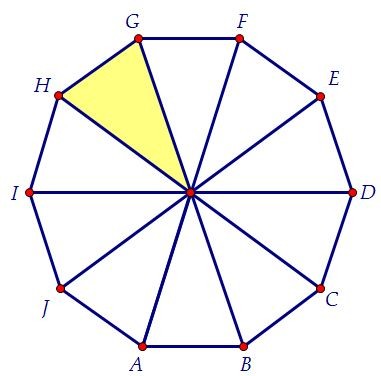 к. строим десятиугольник) с помощью транспортира, т.е. 360°:10=36°. Получаем 10 вершин: A, B, C, D, E, F, G, H, K, L. Соединяем эти вершины, получаем правильный десятиугольник.
к. строим десятиугольник) с помощью транспортира, т.е. 360°:10=36°. Получаем 10 вершин: A, B, C, D, E, F, G, H, K, L. Соединяем эти вершины, получаем правильный десятиугольник.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Сдача сессии и защита диплома – страшная бессонница, которая потом кажется страшным сном. 8924 –
| 7231 – или читать все.91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
- Как начертить десятиугольник
- Как начертить угол без транспортира
- Как построить правильный восьмиугольник
- – циркуль;
- – линейка.
2 способ: Опять же, с помощью циркуля начертите окружность. Центр получившейся окружности обозначьте буквой О. Проведите два перпендикулярных диаметра данной окружности СD и АВ. Разделите один из 4-х радиусов на две равные части. Из рисунка видно, что радиус СО = СМ+МО, где СМ=МО.
Центр получившейся окружности обозначьте буквой О. Проведите два перпендикулярных диаметра данной окружности СD и АВ. Разделите один из 4-х радиусов на две равные части. Из рисунка видно, что радиус СО = СМ+МО, где СМ=МО.
Дальше поставьте ножку циркуля в точку М и начертите окружность радиусом, равным половине радиуса первоначальной окружности. С помощью линейки соедините центр маленькой окружности М с любой из 2-х точек (А или В) на перпендикулярном диаметре. На рисунке центр маленькой окружности соединен сточкой А. Длина, получившегося отрезка АМ будет равна длине стороны десятиугольника. Осталось только сделать раствор циркуля, равный длине отрезка АМ, поставить ножку циркуля в точку А и отметить следующую точку на окружности. Далее переместите ножку циркуля в новую точку и отметьте следующую. И так до тех пор, пока на окружности не появится 10 равноудаленных друг от друга точек.
| Правильный десятиугольник | |||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Сторон и вершин | 10 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| Символ Шлефли | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| Внутренний угол | 144° | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| Симметрия | Диэдрическая ( D 10 <displaystyle D_<10>> ), порядок 20.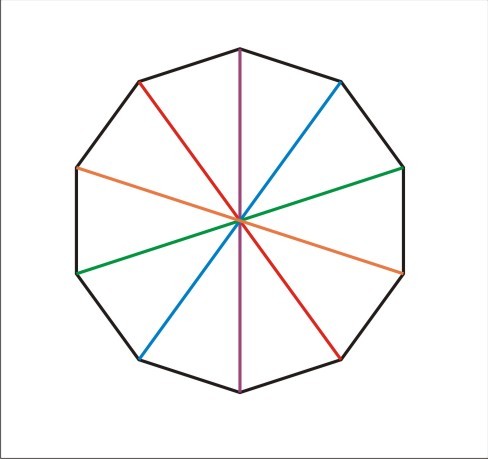 <2>.> <2>.>Альтернативная формула A = 2.5 d t <displaystyle A=2.5dt> , где d – расстояние между параллельными сторонами или диаметр вписанной окружности. В тригонометрических функциях он выражается так:d = 2 t ( cos 3 π 10 + cos π 10 ) , <displaystyle d=2tleft(cos < frac <3pi ><10>>+cos < frac <pi ><10>> и может быть представлен в радикалах как d = t 5 + 2 5 . <displaystyle d=t<sqrt <5+2<sqrt <5>>>>.> Сторона правильного десятиугольника, вписанного в единичную окружность, равна 5 − 1 2 = 1 φ <displaystyle < frac <<sqrt <5>>-1><2>>=< frac <1><varphi >>> , где φ – золотое сечение.Радиус описанной окружности десятиугольника равен R = 5 + 1 2 t , <displaystyle R=<frac <<sqrt <5>>+1><2>>t,> а радиус вписанной окружности r = 5 + 2 5 2 t . <displaystyle r=<frac <sqrt <5+2<sqrt <5>>>><2>>t. Построение [ править | править код ]По теореме Гаусса — Ванцеля правильный десятиугольник возможно построить, используя лишь циркуль и линейку. Иначе его можно построить следующим образом:
Разбиение правильного десятиугольника [ править | править код ]Гарольдом Коксетером было доказано, что правильный 2 m <displaystyle 2m> -угольник можно разбить на m ( m − 1 ) 2 >> ромбов. Для декагона m = 5 , так что он может быть разбит на 10 ромбов.
Пространственный десятиугольник [ править | править код ]
Пентаграммная антипризма с перекрёстом Пространственный десятиугольник — это пространственный многоугольник с десятью рёбрами и вершинами, но не лежащими в одной плоскости. У правильного пространственного десятиугольника все рёбра равны. В трёхмерном пространстве это зиг-заг пространственный декагон, он может быть обнаружен среди рёбер и вершин пентагональной антипризмы, пентаграммной антипризмы, пентаграммной перекрещивающейся антипризмы с той же D5d [2 + ,10] симметрией порядка 20. Его также можно найти в некоторых выпуклых многогранниках с икосаэдрической симметрией. Многоугольники по периметру этих проекций (см. ниже) это пространственные десятиугольники. Многоугольники Петри [ править | править код ]Правильный пространственный десятиугольник — это многоугольник Петри для многих многогранников высших размерностей, как показано на этих ортогональных проекциях на различных плоскостях Коксетера. Оцените статью: Поделитесь с друзьями!начертить десятиугольник угольник — ВидеоПостроение 10 угольника циркулемPavel Kubarkov13-12-2017 Как начертить пятиугольник вписанный в круг или звездаSineD 411-01-2017 Геометрия — Построение десятиугольникаNick Komarov11-03-2018 Построение пятиугольника циркулемPavel Kubarkov13-12-2017 Построение 5 угольника циркулем, метод с кругами КарлайлаPavel Kubarkov22-12-2017 Три способа нарисовать правильный пятиугольникОльга Соколова24-04-2020 Как нарисовать пятиконечную ЗВЕЗДУ с помощью циркуляLostas11-01-2018 Построение правильного пятиугольникаНаталья Турьева20-04-2017 Построение пятиугольникаLes Ruk27-06-2017 Построение 7 угольника циркулем, приближенноеPavel Kubarkov16-12-2017 Как построить правильный шестиугольник. Никита Качесов | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| Внутренний угол | 144 ° | Как и любой правильный многоугольник, чтобы найти внутренний угол, мы используем формулу
(180н – 360) / л. Для десятиугольника n = 10.
См. Внутренние углы многоугольника Для десятиугольника n = 10.
См. Внутренние углы многоугольника |
| Внешний угол | 36 ° | Чтобы найти внешний угол правильного десятиугольника, мы используем тот факт, что внешний угол образует линейная пара с внутренним углом, поэтому в целом он определяется формулой 180-внутренний угол. См. Внешние углы многоугольника |
| Площадь | 7,694 с 2 прибл. | Где S — длина стороны.Чтобы определить точную площадь десятиугольника или любого многоугольника различными методами, см. Площадь правильного многоугольника и Площадь неправильного многоугольника |
Свойства всех декагонов
| Количество диагоналей | 35 | Количество различных диагоналей, возможных для всех вершин.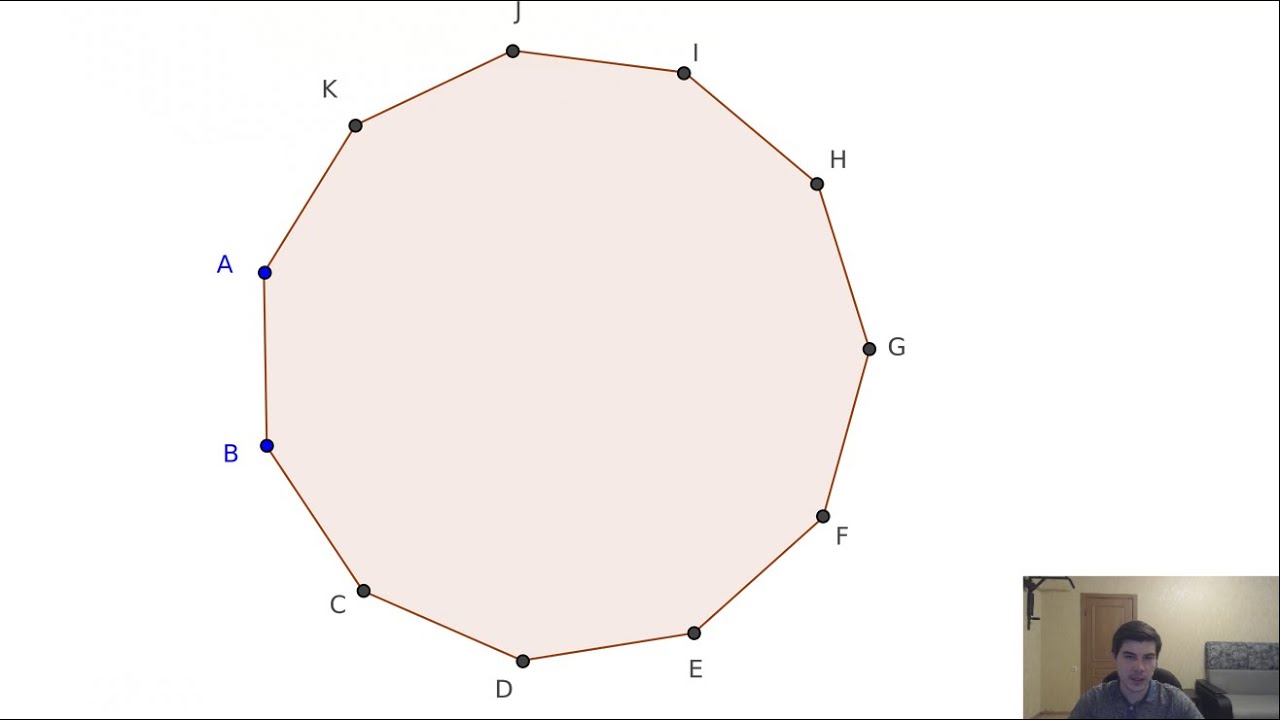 (Обычно ½n (n – 3)).
На рисунке выше нажмите «показать диагонали», чтобы увидеть их.
См. Диагонали многоугольника (Обычно ½n (n – 3)).
На рисунке выше нажмите «показать диагонали», чтобы увидеть их.
См. Диагонали многоугольника |
| Количество треугольников | 8 | Количество треугольников, созданных путем рисования диагоналей из заданной вершины.(В общем n – 2). На рисунке выше нажмите «показать треугольники», чтобы увидеть их. Увидеть треугольники многоугольника |
| Сумма внутренних углов | 1440 ° | Обычно 180 (n – 2) градусов. См. Внутренние углы многоугольника |
Другие полигоны
Общие
Типы полигонов
Площадь различных типов полигонов
Периметр различных типов полигонов
Углы, связанные с многоугольниками
Именованные полигоны
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Обучение детей рисованию геометрических фигур с помощью уроков и руководств по рисованию
Как научить детей геометрическим фигурам и формам
Есть определенные формы, к которым применяются определенные имена. Они часто встречаются в самых простых предметах. Следовательно, хотя эти формы известны под грозным названием геометрических фигур, тем не менее, большинство из этих форм настолько просты, что их можно легко распознать, и при небольшом упражнении в памяти их можно назвать по имени.Самый простой способ для ребенка завязать знакомство — составить и нарисовать их. Их применение будет легко выполнено.
Расскажите детям о фигурах, вырезав следующие фигуры из картона или картона.
пл.
Прямоугольник.
Треугольники (правильный, острый, тупой и равносторонний треугольники).
Круг.
Овал.
Объясните простые геометрические картинки.
Постарайтесь объяснить вопросы, связанные с изучением линий и формы, с помощью простых иллюстраций. Например, ребенок может не понимать значения параллельных линий. Нарисуйте ему маленькую картинку лестницы, показывая, что, как бы далеко ни протянулись линии, они никогда не пересекутся.Затем нарисуйте полузакрытый зонтик и объясните значение сходящихся и расходящихся линий, как показано на рис. 1. выше. Скажите ему, что линии 1, 2 и 3 на иллюстрации зонтика являются сходящимися линиями, когда они приближаются к верхней части зонта, — что сходящиеся линии имеют тенденцию сближаться. С другой стороны, когда упомянутые линии приближаются к ручке, они расходятся, потому что они стремятся все дальше и дальше отдаляться друг от друга.Вспомогательные средства для запоминания названий геометрических фигур
Трапеция, трапеция, ромб и ромб — термины, которые трудно запомнить.![]()
Упражнения для запоминания
Нарисуйте на доске формы, показанные на рис. 2 выше, и попросите учащихся назвать название первой формы.Когда вы ответите правильно, попросите другого ученика назвать вторую фигуру и так до последней. Сотрите фигуры с доски и назовите одну из фигур, попросив ученика нарисовать ее, например, трапецию. Затем попросите ученика нарисовать трапецию и так далее для каждой последующей фигуры.
Многие ученики быстрее запоминают формы, если их значение сочетается с прилагательными, описывающими вид форм. Как следующее:
Линии, используемые на чертеже.
На рис. 6 показаны линии, использованные на чертеже. Их формы и определения следует тщательно запомнить. На рис. 7 показано их применение в виде комбинации и повторения.
Части этого упражнения могут оказаться слишком сложными для многих новичков. В таких случаях упражнения можно временно не выполнять, чтобы заняться позже, когда они станут старше. Линии в примерах сделаны более жирными, чтобы указать их положение.Буквы A, B, C и т. Д. Повторяются на верхней и нижней диаграммах в качестве дополнительной помощи в этом отношении.
Исследование геометрических форм и фигур
Сфера, куб, цилиндр, квадратная призма, полусфера и прямоугольная треугольная призма. Их можно рассматривать в следующем порядке:.
1. Поверхности и грани.
2. Края.
3. Уголки.
Поверхность находится снаружи любого объекта. В случае с кубом, например, мы обнаруживаем, что поверхность ограничена и разбита ребрами и гранями. грань — это ограниченная часть поверхности. Кромка , кромка , образована встречей двух граней.
В случае с кубом, например, мы обнаруживаем, что поверхность ограничена и разбита ребрами и гранями. грань — это ограниченная часть поверхности. Кромка , кромка , образована встречей двух граней.
Проводя пальцами по поверхности одного из твердых тел, зрачок обнаруживает явные различия. Он отмечает ровную или плоскую поверхность, изогнутую поверхность и круглую поверхность. Он обнаруживает, что все они не одинаковой формы, и узнает, что края могут быть изогнутыми или прямыми.
Уголки будут отмечены, а также разница в форме, если ему будет показано, как их изучать. Изучив каждый из них, ученик должен взять вместе сферу и куб, чтобы он мог наблюдать их сходство и различие. Внимательно объясните им значение измерения. Размер — это протяженность в одном направлении. Что касается поверхностей, их различия заметны. Поверхность сферы изогнута одинаково во всех своих частях, а поверхность куба имеет шесть равных плоских граней. Две из этих шести поверхностей, соприкасающиеся друг с другом, образуют ребро, которое является предметом второй темы исследования твердых тел.
Две из этих шести поверхностей, соприкасающиеся друг с другом, образуют ребро, которое является предметом второй темы исследования твердых тел.
У куба двенадцать ребер, а у сферы ни одного.
Что касается углов.
На сфере нет ничего; не может быть углов там, где нет краев. У куба восемь углов. Три или более граней должны соприкасаться, чтобы образовать угол. Углы плоских граней куба — прямые, поэтому на каждом кубе находится двадцать четыре прямых угла.
Цилиндр и квадратная призма.
В целом, точки сходства таковы: размеры одинаковы в каждом.
По поверхности и граням.
Цилиндр имеет как изогнутые, так и плоские поверхности; квадратная призма имеет только плоские поверхности. Что касается краев, цилиндр имеет изогнутые края; квадратная призма, прямые края. Что касается углов, квадратная призма имеет то же количество углов, что и куб; цилиндр не имеет углов. Два куба образуют одну квадратную призму.
Что касается углов, квадратная призма имеет то же количество углов, что и куб; цилиндр не имеет углов. Два куба образуют одну квадратную призму.
Грани параллельны друг другу, если они проходят в одном направлении. Грани перпендикулярны, когда они расположены под прямым углом друг к другу. Квадратный угол будет образован пересечением трех. Грани наклонены друг к другу, когда они образуют углы, отличные от прямых.
Твердые вещества рассматриваются, во-первых, как «целые»; во-вторых, «к поверхностям и граням» и, в-третьих, «к краям».»Кромка образуется в результате встречи двух сторон. Края могут быть изогнутыми или прямыми.
Поверхность сферы изогнута одинаково во всех частях, а поверхность куба состоит из шести равных плоских граней. Когда любые две из этих граней соприкасаются, образуется кромка. Профиль ограничивает видимую часть круглой или изогнутой поверхности. Профили и кромки ограничивают и придают видимую форму граням и частям граней.
Начните с рисования кругов, овалов, прямоугольников и треугольников на рис.8. выше. Теперь позвольте учащемуся построить объекты по этим линиям, как показано на рисунке 9 ниже. Необязательно очень строго придерживаться очертаний.
На рис. 11 ниже круг, овал, квадрат, продолговатый и треугольник на рис. 10 объединены в одно изображение. Попросите учащихся сделать еще один рисунок, на котором указаны эти формы. Скажите ему, что продолговатое изображение может указывать на тело телеги; круг, одно из колес; квадрат, ящик на тележке; овал, мешок муки на ящике.Треугольник может показывать угол наклона крыши дома.
Примеры на рис. 13 выше показывают применение треугольников в качестве ориентира при рисовании различных объектов.
На рис. 14 выше приведены различные примеры применения триангуляции в дизайне и композиции.Не обязательно, чтобы рисунки плотно прилегали к очертаниям треугольников.
Как рисовать треугольники, квадраты, пятиугольники, шестиугольники и Другие многогранные и многогранные формы
Рисование равностороннего треугольника.
Чтобы нарисовать равносторонний треугольник внутри круга. Опишите круг, Рис.А . Не меняя радиуса, поместите точку циркуля в каждую из черных точек, начиная с точки Y (в верхней части круга), и пересекайте круг. Формирование треугольника показано пунктирными линиями.
На рис. B показан более простой способ создания равностороннего треугольника. Начните с любой точки, скажем, с точки A, и опишите сегмент круга. В любой точке, как в точке B, с циркулем того же радиуса пересечь первый сегмент.На пересечении C поместите точку компаса и пересекайте другие кривые, как на B и A. Линии, проведенные от A к B, B к C и C к A, как показано пунктирными линиями, образуют треугольник.
Начните с любой точки, скажем, с точки A, и опишите сегмент круга. В любой точке, как в точке B, с циркулем того же радиуса пересечь первый сегмент.На пересечении C поместите точку компаса и пересекайте другие кривые, как на B и A. Линии, проведенные от A к B, B к C и C к A, как показано пунктирными линиями, образуют треугольник.
Рис. C. Чтобы сделать шестиугольник или шестиконечную звезду. Опишите круг. Из точки A на окружности с помощью циркуля (радиус остается неизменным) пересеките окружность в точке B. Повторите с C, D и так далее, пока точка A не пересечется. Линии, проведенные, как показано пунктирными линиями, от A до B и от B до C, если продолжить до D, E и т. Д., Образуют шестиугольник.
Для шестиконечной звезды нарисуйте линии, как на пунктирных линиях G, линии, как показано на образце пунктирной линии от E до K. Продолжайте таким образом, чтобы сделать шесть частей чертежа.
Чтобы нарисовать квадрат.
Чтобы получить абсолютно точный четырехугольник, действуйте следующим образом: Опишите круг, как на рис. I. Разделите его пополам через центр от A до XX. Сделайте сегмент дуги CC, поместив конец циркуля в X слева.Линия BB проводится таким же образом от X справа. Вертикальная линия, продолженная через круг от пересечения прямых BB и CC и пересекающая горизонтальную линию в точке A, и продолженная до основания круга, образует четыре прямых угла.
На том же чертеже (Рис. 1 и 2 на самом деле являются одним рисунком, но для простоты изображены на двух схемах) описывают дуги окружностей одинакового размера или окружности, помещая острие циркуля. на каждом X.Сегменты встречаются или пересекаются в EEEE. Они также соответствуют окружности исходного круга в 0000, но это не имеет ничего общего с созданием четырехугольника или квадрата. Теперь протяните четыре линии от каждой E до другой, и они коснутся круга в каждой точке X. Эти четыре линии образуют идеальный квадрат.
Эти четыре линии образуют идеальный квадрат.
Другие формы, полученные с помощью этой операции для создания шестиугольника.
Сделать восьмиугольник.
Продлите линии от каждой точки E до центра точки A (рис.2). Теперь нарисуйте восемь линий, как показано пунктирной линией от X до F, что дает одну часть восьмиугольника.
Создание равностороннего треугольника.
Треугольник, у которого все стороны равной длины — проведите линию GG, параллельную XX, в верхней части круга. Продлите линии от центра A через 00 (как показано на рис. 2) до линии GG, и в результате жирными линиями будет показана равносторонняя сторона.
Пентагон.
Чтобы построить пятиугольник, нарисуйте части трех окружностей как A A, B B и C C, как на рис. I. Затем проведите вертикальную линию D D. Затем косые линии EE и F F. От пересечения прямой EE в верхней части окружности CC опишите отрезок окружности J. На том же чертеже (как на рис. 2) постройте пятиугольник, показанный жирными линиями G, H, I и J.
I. Затем проведите вертикальную линию D D. Затем косые линии EE и F F. От пересечения прямой EE в верхней части окружности CC опишите отрезок окружности J. На том же чертеже (как на рис. 2) постройте пятиугольник, показанный жирными линиями G, H, I и J.
Другой Пентагон.
Метод рисования пятиугольника путем определения точек, необходимых для образования десятиугольника: Опишите круг, как в A.Затем полукруг, как показано пунктирными линиями (тот же радиус, что и большой круг). Затем вертикальная линия; рядом пунктирная горизонтальная линия. Теперь опишите маленький кружок; теперь нижняя горизонтальная линия. Протяните линию от пересечения вертикальной линии и вершины маленького круга, а затем до пересечения с пунктирной горизонтальной линией. Теперь опишите сегмент круга, начиная с пересечения наклонной линии и нижней горизонтальной линии и касаясь маленького круга. Черные точки на наклонной линии указывают расстояние, равное десятой части десятиугольника, как показано на C и B. Используйте чередующиеся пробелы, чтобы сформировать пятиугольник, как в точке B, или пятиконечную звезду в точке C. Это упражнение не так утомительно, как кажется.
Используйте чередующиеся пробелы, чтобы сформировать пятиугольник, как в точке B, или пятиконечную звезду в точке C. Это упражнение не так утомительно, как кажется.
Бревна как модели цилиндров.
Из небольших бревен или веток деревьев, нарезанных на отрезки подходящей длины, получается превосходная модель-S: длина каждой части может варьироваться от одного до двух диаметров.Выпилить участки, как показано на рис. 2; то есть отрежьте одну восьмую, четверть, одну треть или половину четырех бревен, как в A, B, C, D. Рис. 1 сделан, чтобы показать, что те же методы используются для рисования кубиков. , призмы и другие предметы квадратной формы, как и изогнутые. Принцип перспективы одинаков для всех.
Бревна могут быть вытянуты в различных положениях, в виде вертикального, горизонтального, отступающего, а также правого и левого отклоняющегося цилиндра.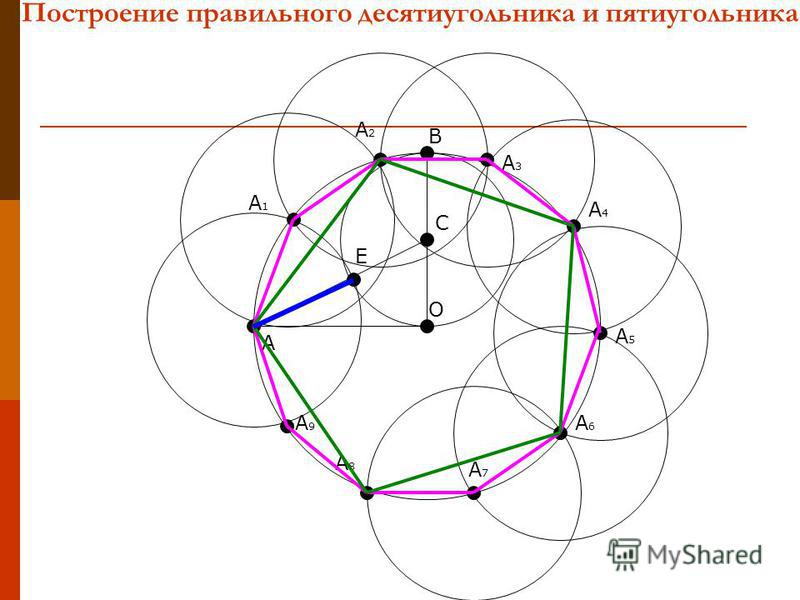
Заменитель циркуля-карандаша
Возьмите полоску картона размером примерно 1 x 4 дюйма. Проколите отверстия с интервалом в N дюймов по середине его длины. Вставьте булавку в картон и бумагу для рисования в доску. Проденьте острие карандаша в любое отверстие, и круги будут легко сделаны.Схема объясняет его конструкцию и использование.
Цель состоит в том, чтобы найти количество диагоналей, которое можно провести внутри десятиугольника. Сколько диагоналей можно нарисовать внутри десятиугольника? КУРС 2 УРОК 7-6 Запомните.
Презентация на тему: «Цель состоит в том, чтобы найти количество диагоналей, которые можно нарисовать внутри десятиугольника. Сколько диагоналей можно нарисовать внутри десятиугольника? КУРС 2, УРОК 7-6 Запомните. » — стенограмма презентации:
» — стенограмма презентации:
1 Цель состоит в том, чтобы найти количество диагоналей, которое можно нарисовать внутри десятиугольника.Сколько диагоналей можно нарисовать внутри десятиугольника? КУРС 2 УРОК 7-6 Помните, что диагональ — это сегмент, соединяющий две вершины, которые не являются конечными точками одной и той же стороны многоугольника. На диаграмме ниже показаны все диагонали, которые можно нарисовать внутри каждого показанного многоугольника. 3 стороны 4 стороны 5 сторон 6 сторон Нарисуйте схему и найдите узор 7-6
2
(продолжение) КУРС 2 УРОК 7-6 Данные в таблице показывают, что формула для количества диагоналей, которые могут быть нарисованы внутри многоугольника с n сторонами, равна Для десятиугольника n = 10.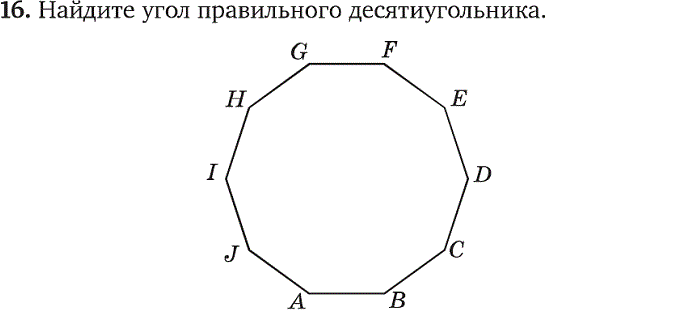 n (n — 3) 2 10 (10 — 3) 2 = = 35 10 7 2 Тридцать пять диагоналей можно провести внутри десятиугольника. Составьте таблицу, чтобы упорядочить информацию из диаграммы. диагонали сторон 3030 4242 5555 6969 Нарисуйте схему и найдите узор 7-6
n (n — 3) 2 10 (10 — 3) 2 = = 35 10 7 2 Тридцать пять диагоналей можно провести внутри десятиугольника. Составьте таблицу, чтобы упорядочить информацию из диаграммы. диагонали сторон 3030 4242 5555 6969 Нарисуйте схему и найдите узор 7-6
3 (продолжение) КУРС 2 УРОК 7-6 Чтобы проверить, можно ли провести 35 диагоналей внутри десятиугольника, нарисуйте диаграмму. Всего 35 диагоналей. Нарисуйте схему и найдите узор 7-6
4 КУРС 2 УРОК 7-6 Решите, нарисовав диаграмму и ища образец.Как показано, внешние углы треугольника являются дополнением к внутренним углам. Какова сумма внешних углов правильного шестиугольника? 360º Нарисуйте схему и найдите узор 7-6
Полигоны — Десятиугольники
Свойства декагонов, внутренние углы декагонов
| Полигоны: Свойства декагонов | |||
Углы десятиугольника: | |||
| |||
| Обычные десятиугольники: | |||
| Свойства правильных десятиугольников: | 9044 одинаковые длины ) и все внутренние углы одинакового размера (совпадают).Чтобы найти меру углов, мы знаем, что сумма всех углов составляет 1440 градусов (сверху) … И есть десять углов … Итак, мера угол правильного десятиугольника — 144 градуса. | ||
| Измерение центральных углов правильного десятиугольника: | |
Найти меру правильного угла центрального угла , сделайте круг посередине. .. Окружность составляет 360 градусов вокруг … Разделите это на десять углов … .. Окружность составляет 360 градусов вокруг … Разделите это на десять углов … Итак, центральный угол правильного десятиугольника равен 36 градусам. | |
определение десятиугольника в The Free Dictionary
Десятиугольник ясно показывает, что на практике правительство не намерено привлекать прямые иностранные инвестиции Между тем, Ассоциация производителей цемента (CMA) Непала на прошлой неделе организовала дискуссию программистов о проблемах цементной промышленности в стране, где производители пытались убедить министра промышленности , «Матрика Прасад Ядав» по торговле и снабжению и соответствующие департаменты окружающей среды, лесного хозяйства, промышленности и стандартов, запрещающие прямые иностранные инвестиции (ПИИ) в этот сектор.Sterling Bank Plc стал партнером Decagon Software Engineering в повышении квалификации 5000 нигерийских выпускников, чтобы преодолеть разрыв в спросе на инженеров-программистов. Мухаммад Фарук вместе с председателем Decagon Pakistan (Private) Limited г-ном КАРАЧИ — счастливая церемония розыгрыша была проведена высшим руководством В состав NBP входят руководители SEVP / группы Тарик Джамал, Джамал Бакир и ИТ-директор Шахид Саид, глава группы по платежным сервисам и цифровому банкингу Мухаммад Фарук, а также председатель Decagon Pakistan (Private) Limited Азиз Кассамали и представители UnionPay International.Karachi — The First Women Bank Limited и Decagon Pakistan (Private) Limited, владелец Golootlo, подписали в среду в Карачи соглашение, которое позволит клиентам FWBL пользоваться скидками через приложение Golootlo. Точечный метод с использованием измерителя потенциала точки росы WP4 (DECAGON DEVICES, 2003). На северном винограднике также проводятся измерения профиля влажности почвы в шести местах с использованием диэлектрических датчиков потенциала воды Decagon (MPS-2 Decagon Pullman Washington) на глубинах приблизительно 5, 50, 90 и 125 см, с двумя большими датчиками влажности почвы Decagon 10HS на глубине 45 см.
Мухаммад Фарук вместе с председателем Decagon Pakistan (Private) Limited г-ном КАРАЧИ — счастливая церемония розыгрыша была проведена высшим руководством В состав NBP входят руководители SEVP / группы Тарик Джамал, Джамал Бакир и ИТ-директор Шахид Саид, глава группы по платежным сервисам и цифровому банкингу Мухаммад Фарук, а также председатель Decagon Pakistan (Private) Limited Азиз Кассамали и представители UnionPay International.Karachi — The First Women Bank Limited и Decagon Pakistan (Private) Limited, владелец Golootlo, подписали в среду в Карачи соглашение, которое позволит клиентам FWBL пользоваться скидками через приложение Golootlo. Точечный метод с использованием измерителя потенциала точки росы WP4 (DECAGON DEVICES, 2003). На северном винограднике также проводятся измерения профиля влажности почвы в шести местах с использованием диэлектрических датчиков потенциала воды Decagon (MPS-2 Decagon Pullman Washington) на глубинах приблизительно 5, 50, 90 и 125 см, с двумя большими датчиками влажности почвы Decagon 10HS на глубине 45 см. >
>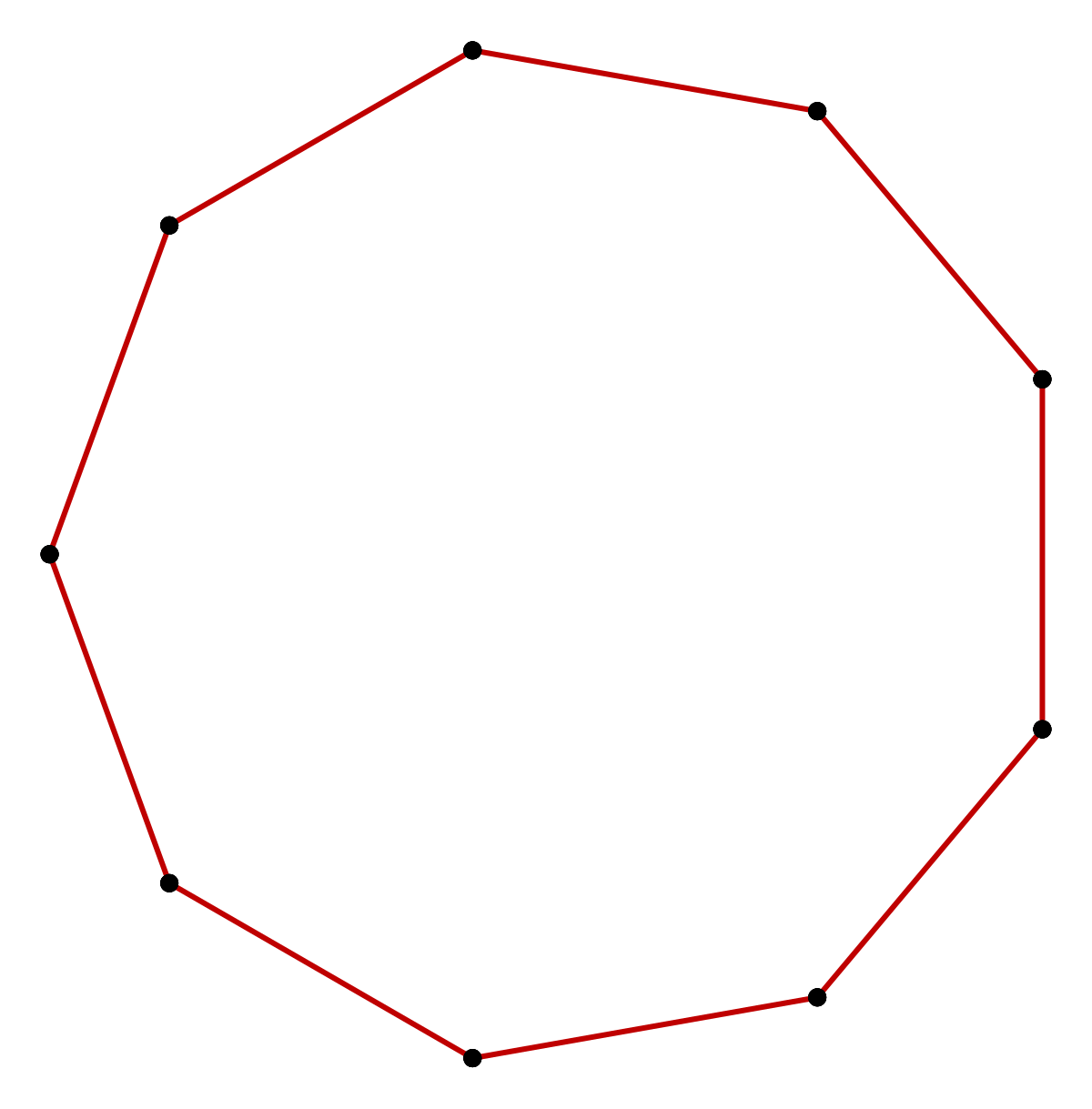 У пространственного зиг-заг десятиугольника вершины чередуются между двумя параллельными плоскостями.
У пространственного зиг-заг десятиугольника вершины чередуются между двумя параллельными плоскостями.
 Пропорции в правильном пятиугольнике
Пропорции в правильном пятиугольнике  Обучение — Znaika TV. Знайка.ру
Обучение — Znaika TV. Знайка.ру Существует большое количество весьма простых задач подобного рода. Их решение сводится к модифицированию или комбинированию уже известных примеров. Однако есть и такие, над решением которых нужно подумать. Одной из нетривиальных является задача о том, как построить правильный десятиугольник.Вам понадобится
Существует большое количество весьма простых задач подобного рода. Их решение сводится к модифицированию или комбинированию уже известных примеров. Однако есть и такие, над решением которых нужно подумать. Одной из нетривиальных является задача о том, как построить правильный десятиугольник.Вам понадобится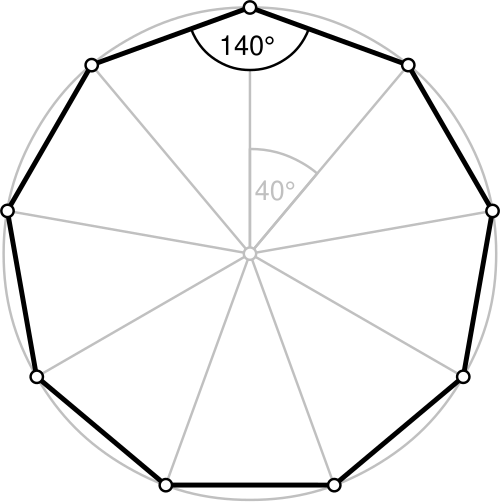 Вычертите окружность. Не меняя раствора ножек, установите иглу циркуля в точку P1. Вычертите окружность. Постройте отрезок прямой, проходящий через точки пересечения начерченных окружностей. Он пройдет также и через точку O. Обозначьте точки пересечения данного отрезка с окружностью O как B и P2.
Вычертите окружность. Не меняя раствора ножек, установите иглу циркуля в точку P1. Вычертите окружность. Постройте отрезок прямой, проходящий через точки пересечения начерченных окружностей. Он пройдет также и через точку O. Обозначьте точки пересечения данного отрезка с окружностью O как B и P2. Сделайте циркулем засечку на окружности O в направлении движения по часовой стрелке (игла циркуля находится в точке A). Обозначьте полученную точку E. Не меняя раствора ножек, переместите иглу в точку E. Сделайте еще одну засечку. Обозначьте току как F. Действуя подобным образом, последовательно постройте точки G и H. Попарно соедините точки A, E, F, G, H отрезками. Фигура AEFGH является правильным пятиугольником.
Сделайте циркулем засечку на окружности O в направлении движения по часовой стрелке (игла циркуля находится в точке A). Обозначьте полученную точку E. Не меняя раствора ножек, переместите иглу в точку E. Сделайте еще одну засечку. Обозначьте току как F. Действуя подобным образом, последовательно постройте точки G и H. Попарно соедините точки A, E, F, G, H отрезками. Фигура AEFGH является правильным пятиугольником.
 Правильный выпуклый десятиугольник представляет собой тонкую и элегантную форму с 10 внешними углами по 36 °, 10 внутренними углами по 144 ° и 10 вершинами (пересечения сторон).
Правильный выпуклый десятиугольник представляет собой тонкую и элегантную форму с 10 внешними углами по 36 °, 10 внутренними углами по 144 ° и 10 вершинами (пересечения сторон).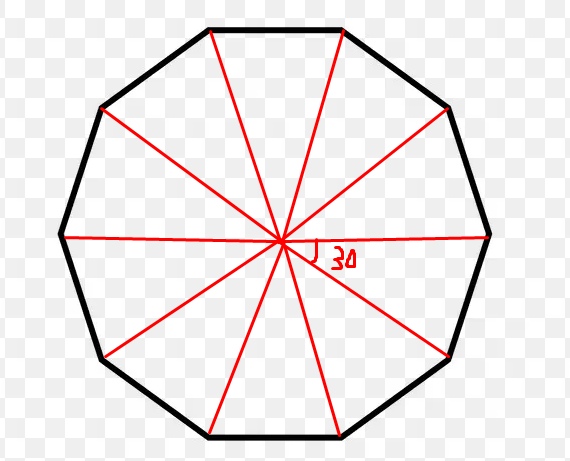

 » — стенограмма презентации:
» — стенограмма презентации:  ..
..