Что можно нарисовать на клетчатой бумаге: Рисунки на бумаге в клетку карандашом (32 фото) 🔥 Прикольные картинки и юмор

Рисуем на клетчатой бумаге – конспект урока – Корпорация Российский учебник (издательство Дрофа – Вентана)

Разработки уроков (конспекты уроков)

Линия УМК М. И. Башмакова. Математика (1-4)

Математика

Данный план урока является частью сервиса «Классная работа»*

Внимание! Администрация сайта rosuchebnik.ru не несет ответственности за содержание методических разработок, а также за соответствие разработки ФГОС.

Цель урока

Развитие пространственных представлений: различение направлений «право» и «лево» в пространстве и на клетчатом листе бумаги.

Задачи урока

Способствовать формированию умений различать направления: вправо, влево, вверх, вниз.

Формировать умение определять положение предмета в пространстве.

Формировать умение устанавливать соответствие между описанием линии и её изображением.

Формировать умение ориентироваться на клетчатом листе бумаги.

Формировать умение выполнять задание, следуя инструкции учителя.

Развивать пространственные представления, графические навыки, логическое мышление.

Способствовать развитию математической речи учащихся.

Виды деятельности

Определение направления движения: вправо, влево, вверх, вниз.

Определение положения предмета: справа, слева, вверху, внизу.

Установление соответствия между описанием линии и её изображением.

Ориентация на клетчатом листе бумаги.

Выполнение рисунка в тетради в соответствии с описанием.

Ключевые понятия

Направление движения, вправо, влево, вверх, вниз.

План урока

№	Название этапа	Методический комментарий
1	1. Мотивация к учебной деятельности	Работа с заданием № 1 учебника. Задание выполняется устно. Оно направлено на повторение понятий «право» и «лево». Тренировка в различении правой и левой руки с опорой на рисунок. Учитель. Покажите, в какой лапке Винни-Пух держит горшочек с мёдом. (Дети поднимают вверх правую руку.) Какая это рука? (Правая.) Покажите, где Пятачок держит воздушный шарик. (Дети поднимают вверх левую руку.) Какая это рука? (Левая.) Работа с интерактивным заданием. При выполнении задании ученики сначала определяют, какая рука является правой и какая — левой у мальчика и у девочки, а затем вставляют рисунки с изображением предметов в пропуски на рисунке в соответствии с инструкцией.
2	2. Актуализация знаний	Работа с заданием № 2 учебника. Работа в паре. Задание направлено на закрепление умения различать правую и левую руку. Учащиеся выполняют задание самостоятельно, учитель помогает тем, кто испытывает трудности. Работа с интерактивным заданием. При выполнении задания отрабатываются понятия «направо» и «налево». Дети рассматривают стрелки на рисунке и закрашивают их разными цветами в соответствии с инструкцией. Дополнительные вопросы: Почему некоторые стрелки не закрашены? (Они не указывают ни направо, ни налево.) В каком направлении они указывают? (Вниз, вверх.)
3	3. Закрепление	Работа с интерактивным заданием. Задание подготовительное к введению движения по клеткам в разных направлениях: вверх, вниз, вправо, влево. Учащиеся раскрашивают предметы на картинке в соответствии с их расположением. Работа с заданием № 3 учебника. При выполнении задания происходит ориентирование на странице учебника (вверх, вниз, вправо, влево), развитие речи. Описание пути зайчика даётся только с точки зрения наблюдателя (ученика). При работе в паре учащиеся подготавливают друг для друга вопросы. Если при описании, которое даёт ученик, зайчик не попадает ни к одному из нарисованных объектов, то можно отметить точку, в которую он пришёл, или можно продолжить путь зайчика и привести его к кочану капусты, к морковке и др.
4	4. Самостоятельная работа	Работа с заданием № 4 учебника. Ориентирование на странице тетради, развитие речи. Учащиеся чертят по сторонам клеток линии по описанию пути. Учитель может продиктовать любую цепочку шагов или кольцевой путь, при котором зайчик возвращается в исходную точку. Работа с интерактивным заданием. Учащиеся считают цепочку шагов на каждом рисунке и проговаривают весь путь (один шаг соответствует одной клетке). Например, один шаг влево, один шаг вверх, один шаг влево, один шаг вверх; получается четыре шага. Ученики отмечают дорожку, состоящую из пяти шагов. Можно обратить внимание детей, что на рисунках изображены ломаные линии, число шагов равно числу звеньев ломаной.
5	5. Итог урока	Работа с интерактивным заданием. Учащиеся считают цепочку шагов на каждом рисунке, проговаривают весь путь и отмечают самую длинную дорожку, которая занимает наибольшее число клеток.

Хотите сохранить материал на будущее? Отправьте себе на почту

в избранное

Только зарегистрированные пользователи могут добавлять в избранное.

Войдите, пожалуйста.

Исследование одной задачи. Квадраты на клетчатой бумаге.

 

              Исследование одной задачи

Квадраты на клетчатой бумаге

ХАФИЗОВ ДАНИЯР

Республика Татарстан, Тукаевский район, село Кузкеево,

МБОУ «Кузкеевская СОШ», 6 класс

Научный руководитель: Мингалимова Резеда Рашитовна

2014

Оглавление.

1.Введение………………………………………………………………………………………………………………..3

2.Площади «прямых квадратов»………………………………………………………………………………..4

3.Теорема Пифагора для равнобедренных прямоугольных треугольников………………….4

4. Площадь «светлого» квадрата………………………………………………………………………………..5

5. Заключение……………………………………………………… …………………………………………………..6

Введение.

Задача взята из упражнения  замечательной книжки И.Ф. Шарыгина, Л.Н. Ерганжиевой «Наглядная геометрия. 5-6 классы», М., Дрофа, 2008: построить на клетчатой бумаге квадраты с вершинами в узлах сетки площадью 1, 2, 4, 5, 8, 9, 10, … клеток. Задачи на нахождение площадей квадрата, прямоугольника, а так же прямоугольного треугольника решаются в начальных классах. В данной работе ученик рассматривает квадраты, вершины которых лежат в вершинах клеток, площади которых 1, 2, 4, 8, 9, 13, 25, 26 клеток. При исследовании использовал факты, изложенные в теореме Пифагора для равнобедренных прямоугольных треугольников, для прямоугольных треугольников. План работы:

Цель нашей работы – выявить, квадраты какой площади можно так построить, а какой – нельзя.

Основная часть.

Задача. Квадраты какой площади можно нарисовать на клетчатой бумаге? (Вершины должны лежать в вершинах клеток.)

 Для начала попробуем нарисовать квадраты площадью 1, 2, 4, 5, 8, 13, 26 клеток.

1. Квадраты нарисованы прямо:

Построим несколько квадратов с вершинами в узлах сетки и найдем их площади. Пусть сторона одного квадратика сетки равна 1клетке.

Их площадь найти легко: это квадраты длин их сторон, а стороны равны целому числу клеток. Площади прямых квадратов – это квадраты целых чисел: 1, 4, 9, 16, 25 и т.д.

Немного усложним задачу.

Нарисовать квадрат, площадь которого 2, 8, 13, 26 клеток.

Рассмотрим частный случай. Составим мозаику из цветных и светлых треугольников.  Для первого случая возьмем прямоугольные, равнобедренные треугольники. Достаточно взглянуть на мозаику и убедиться: S=c2, где c2=2a2 .Квадрат, построенный на длинной стороне содержит 4 треугольника, а на каждой из равных сторон построен квадрат, содержащий 2 треугольника.

Для доказательства общего случая возьмем квадрат со стороной а+b и изобразим четыре прямоугольных треугольника со сторонами a и b, как показано на рисунке 1. «Смотри!». И действительно, взглянув на эти рисунки, видим, чтобы найти площадь квадрата со стороной с,  надо из площади прямого квадрата вычесть 4 площади закрашенных прямоугольных треугольников, т.е. 2ab. Эти треугольники одинаковые. Если расположить эти треугольники, как показано на рис.2, то получится два квадрата, стороной a и b. Площадь одного квадрата равна a2, а второго ─ b2. Сумма их площадей как раз равна площади квадрата со стороной с, потому что это площадь большого квадрата без тех же четырех прямоугольных треугольников.

Значит,

S=a2+b2.

Если сторону «светлого» квадрата обозначить через c, то его площадь S=c2. Поэтому c2=a2+b2.(рис.1), что и составляет утверждение теоремы Пифагора.

Можно нарисовать квадрат, площадь которого 2, так как 2=1+1.

Если площадь равна 8, то a= 2, b=2.

Какими же числами может выражаться площадь «светлого» квадрата с вершинами в узлах сетки? Это такие числа, которые можно представить в виде суммы двух квадратов целых чисел. Например,

13=4+9

20=16+4

26=1+25

50=25+25.

Заключение.

Мне интересно было исследовать, квадраты какой площади можно так построить, а какой – нельзя. Например, число31нельзя представить в виде суммы квадратов целых чисел. Оказывается, все простые числа, кроме 2, представимые в виде а2 + b2, представимы в виде 4п + 1. И наоборот: все простые числа, представимые в виде 4п + 1, представимы в виде а2 + b2. Но это другая исследовательская работа. 

Список использованной литературы.

1. Савин А.П. Энциклопедический словарь юного математика. – М.:Педагогика, 1989. -352 с.: ил.
2. Сгибнев А.И. Исследовательские задачи для начинающих.- М.: МЦМНО, 2013.- 120 с.
3. Шарыгин И. Ф., Ерганжиева Л. Н.«Наглядная геометрия. 5-6 классы», М., Дрофа, 2008.

Создание шаблонов для рисования на миллиметровой бумаге | Austin Artists Market

Изучите некоторые элементы дизайна — цвет, форму и повторение — раскрашивая на миллиметровой бумаге.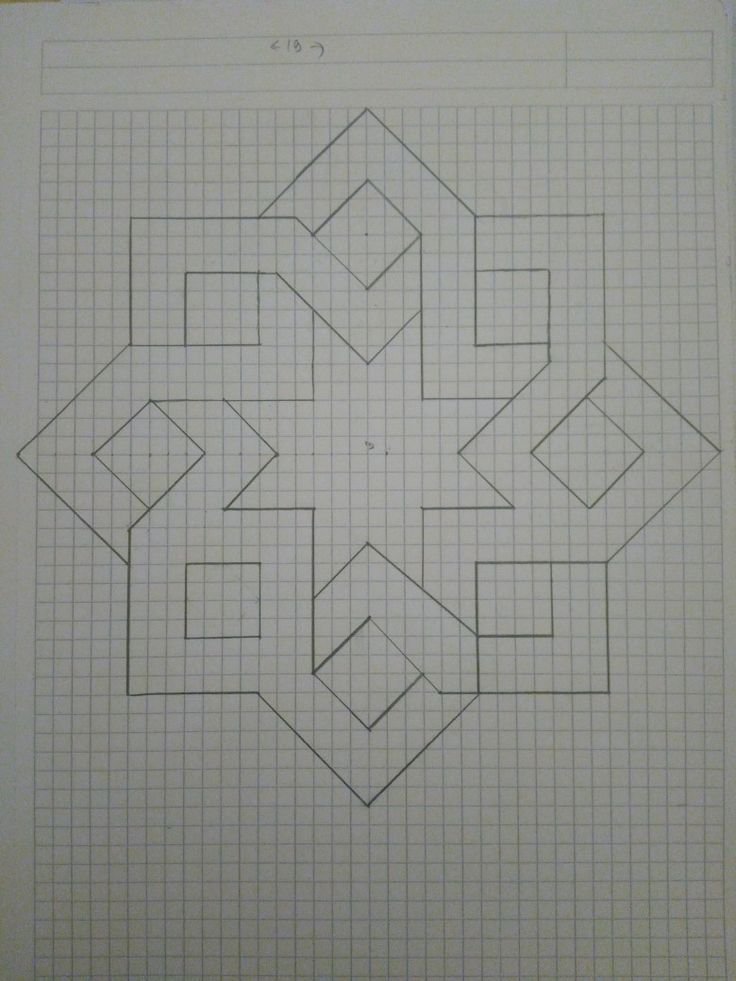

Раскрашивание рисунков на миллиметровой бумаге похоже на раскраску произвольной формы. Вы получаете некоторые рекомендации, но вы решаете, как будет выглядеть готовый дизайн.

Миллиметровая бумага для вашего художественного проекта по созданию выкройки

Все миллиметровки разные. Некоторые сетки содержат больше квадратов в дюйме. В канцелярском магазине вы можете найти бумагу с четырьмя квадратами на дюйм, пятью квадратами на дюйм или шестью квадратами на дюйм. Чем меньше квадратов в дюйме, тем больше квадраты. Большие квадраты легче раскрашивать. Меньшие квадраты позволяют детализировать узоры, но для их завершения требуется гораздо больше времени.

Вы будете заполнять всю страницу, что займет примерно час, если вы используете миллиметровую бумагу с четырьмя квадратами на дюйм.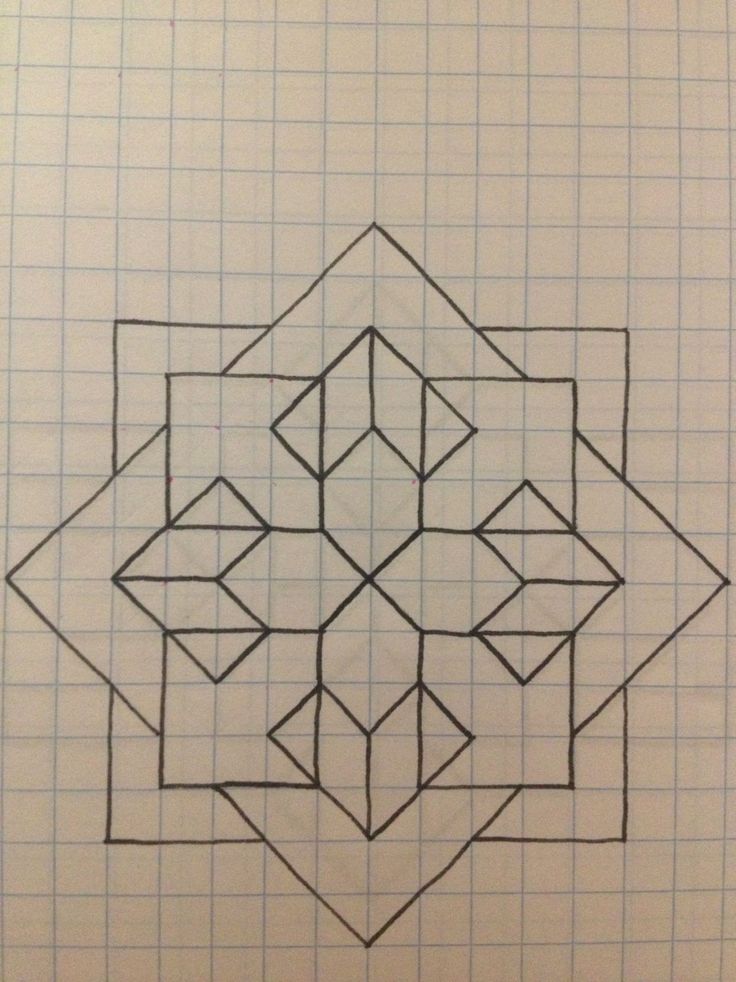 Если вы раскрасите узоры по всей странице, ваше окончательное произведение будет выглядеть интереснее, и вы замаскируете линии графика.

Художественный проект «Раскрашивание узора»

Вам нужно будет раскрасить миллиметровку цветными карандашами или маркерами с тонким наконечником. Если вы используете карандаши, имейте под рукой точилку, так как вам понадобится острие. Не беспокойтесь о раскрашивании за пределами линий. При общем виде изделия это не будет заметно.

Создание рисунков в рамках вашего художественного проекта

Используйте формы квадратов для создания различных узоров. Не обязательно размещать шаблон на всю страницу. Повторение определенного рисунка не менее трех раз делает его образцом.

Полосы (горизонтальные или вертикальные)

Раскрасьте узор из одной коробки тремя, чередуя два или три цвета, чтобы получились полосы. Вы можете сделать более длинные полосы, особенно если вы используете миллиметровую бумагу с более чем четырьмя квадратами на дюйм.

Шахматная доска

– Чередуйте два цвета вдоль одной линии. В следующей строке (строке или столбце) измените цветовую схему, сдвигая ее на единицу, чтобы цвета располагались в шахматном порядке. Попробуйте сделать узор в шахматном порядке по диагонали.

Разрезанные коробки

Проведите диагональную линию через коробку. Раскрасьте верхнюю часть одним цветом, а нижнюю — другим. Повторите узор не менее трех раз по ряду, столбцу или по диагонали.

Крошечные квадраты

Разделите коробку на четыре части, нарисовав букву «t» или «x» внутри каждой коробки. Используйте два или четыре цвета для украшения. Повторите в полосе, квадрате или прямоугольной части миллиметровки.

Мини-фигуры

Нарисуйте ромб или круг внутри квадрата сетки. Раскрасьте фигуру одним цветом, а пространство вокруг фигуры другим цветом.

Крупные фигуры

Раскрасьте несколько прямоугольников так, чтобы область напоминала квадратное сердце, медведя, дерево, рыбу и т. д. Закрасьте фон сплошным цветом.

Words

Раскрась блоки, чтобы составить свое имя.

Сплошные цвета

Раскрашивание квадрата или прямоугольника сплошным цветом.

Дополнительные советы по раскрашиванию узоров

Почти любой узор, который вы можете сделать, используя квадраты в качестве ориентира, можно сделать, разделив один квадрат на четыре части или раскрасив два или четыре квадрата вместе и рассматривая их как большой квадрат.

Вы можете обнаружить, что некоторые узоры, которые вы создаете, оставляют вокруг себя странные формы. Раскрасьте фигуры сплошным цветом или раскрасьте каждую коробку своим цветом. С таким количеством цветов и узоров на вашей картинке эти странные формы будут сливаться воедино.

Сколько узоров можно использовать, раскрашивая целый лист миллиметровки? Интересная часть проекта заключается в том, чтобы использовать свое творчество и открывать больше узоров, чем полосы, квадраты, крошечные квадраты или другие, упомянутые здесь. После создания шаблона на миллиметровой бумаге попробуйте рисовать каракули, рисовать с помощью трафаретов и рисовать абстрактными формами.

Нежелательный эффект миллиметровки (Microsoft Word)

Обратите внимание: Эта статья предназначена для пользователей следующих версий Microsoft Word: 2007, 2010, 2013 и 2016. Если вы используете более раннюю версию (Word 2003 или более раннюю),

этот совет может вам не подойти . Чтобы просмотреть версию этого совета, написанную специально для более ранних версий Word, нажмите здесь: Нежелательный эффект миллиметровой бумаги.

Автор Allen Wyatt (последнее обновление 19 июля 2022 г.)
Этот совет относится к Word 2007, 2010, 2013 и 2016

---

Тревор заметил, что две системы в его офисе совсем недавно продемонстрировали такое же странное поведение . Когда они начинают новый сеанс работы с Word, он открывается с эффектом «миллиметровки» на экране. Он задается вопросом, почему это произошло, и как они могут это отключить.

Есть несколько возможных причин, почему это произошло. Наиболее вероятная причина в том, что была включена сетка рисования. Выполните следующие действия, чтобы отключить его:

1. Убедитесь, что на ленте отображается вкладка «Вид».
2. Снимите флажок «Сетка» в группе «Показать/скрыть».

Если вы обнаружите, что сетка рисования не была включена изначально, проблема может быть связана с установленным в системе фоновым изображением. Вы можете избавиться от любого фонового изображения, выполнив следующие действия:

1. Отобразите вкладку «Макет страницы» на ленте, если вы используете Word 2007 или Word 2010. Для Word 2013 и Word 2016 отобразите вкладку «Дизайн» на ленте.
2. Щелкните Цвет страницы в группе Фон страницы. Word отображает раскрывающуюся палитру параметров.
3. Щелкните Нет цвета.

Если эффект миллиметровки все еще виден, выйдите из Word и используйте инструменты Windows, чтобы найти файл шаблона Normal.

Переименуйте его во что-нибудь другое (например, OldNormal.dotx), а затем перезапустите Word. Если проблема исчезнет, ​​то вы знаете, что это связано с некоторыми настройками, хранящимися в вашем шаблоне Normal. Это может помочь вам отследить виновника, или вы можете просто позволить Word восстановить новый файл шаблона Normal для вас.

Наконец, возможно, у вас установлено какое-то стороннее дополнение, вызывающее эффект. Проверьте свои надстройки и, если вы их видите, отключите их и перезапустите Word.

WordTips — ваш источник недорогого обучения работе с Microsoft Word. (Microsoft Word — самая популярная в мире программа для обработки текстов.) Этот совет (6068) относится к Microsoft Word 2007, 2010, 2013 и 2016. Вы можете найти версию этого совета для старого интерфейса меню Word здесь: Нежелательный эффект миллиметровки .

Биография автора

Allen Wyatt

На его счету более 50 научно-популярных книг и множество журнальных статей, Аллен Вятт является всемирно признанным автором. Он является президентом Sharon Parq Associates, компании, предоставляющей компьютерные и издательские услуги. Узнайте больше об Аллене…

Первое и последнее слово в Word! Бестселлер Для чайников Автор Дэн Гукин возвращается к своей обычной веселой и дружелюбной откровенности, чтобы показать вам, как ориентироваться в Word 2013. Тратьте больше времени на работу и меньше на попытки разобраться во всем этом! Выезд Word 2013 для чайников уже сегодня!

Подписаться

БЕСПЛАТНАЯ УСЛУГА: Получайте подобные советы каждую неделю в WordTips, бесплатном информационном бюллетене по продуктивности. Введите свой адрес и нажмите «Подписаться».

Просмотреть последний информационный бюллетень.

(Ваш адрес электронной почты никому никогда не передается.)

Комментарии

Этот сайт

Есть версия Word, которая использует ленточный интерфейс (Word 2007 или более поздняя версия)?

Этот сайт для вас! Если вы использовать более раннюю версию Word, посетите наш сайт WordTips посвящен интерфейсу меню.