Что можно нарисовать из круга: Что можно нарисовать, если за основу взять круг

Как проще отрисовать круг через SVG?

Вопрос задан 1 год 6 месяцев назад

Изменён 1 год 6 месяцев назад

Просмотрен 830 раз

Paths в SVG — универсальный и мощный инструмент. Но вот отрисовать в нем такую фигуру как круг — задача не такая и простая. Казалось бы есть A (Arc), но я лично смог нарисовать круг только с помощью двух дуг. При этом центр круга нигде не указан, он лежит по середине конечных точек этих дуг. Для контроля добавил белую линию.

<svg xmlns="http://www.w3.org/2000/svg">
    <path d="M40 100 A 50 50 0 0 1 140 100
                     A 50 50 0 0 1 40 100"
       stroke="black" fill="rgb(180,180,255)"/>        
    <line x1="40" y1="100" x2="140" y2="100" stroke="white"/>
</svg>   

Можно нарисовать круг с помощью двух кубических Безье.

Примерно круг в моем случае))

<svg xmlns="http://www.w3.org/2000/svg">
    <path d="M40 100 C 40 34 140 34 140 100
                     C 140 166 40 166 40 100"
       stroke="black" fill="rgb(180,180,255)"/>        
    <line x1="40" y1="100" x2="140" y2="100" stroke="white"/>
</svg>    

Есть ли способ нарисовать круг проще именно с помощью строки path, так чтобы она состояла из одной кривой?

2

Согласен с комментарием от @Alexey Ten

Нет, или я такого не знаю. Две дуги это самое простое и понятное из того что я видел

Ответил бы точно так же.
Мотивация вопроса понятна, так как animateMotion, например не работает с circle, а только с path, реализующий форму круга.

Не знаю, будет ли проще решение с помощью векторного редактора

Итак по шагам:

• В векторном редакторе, наример Inkscape выбираем в боковом меню инструмент — рисовать круги, эллипсы и удерживая shift рисуете из центра круг. Сохраняете файл и копируете формулу path

Но, вам никогда не удастся нарисовать идеальный круг, он будет иметь, хоть немного форму эллипса с разными rx и ry

Другой способ

• Пишите файл svg с нужными координатами центра и размером радиуса окружности

<svg  xmlns="http://www.w3.org/2000/svg"  xmlns:xlink="http://www.w3.org/1999/xlink"
         viewBox="0 0 300 300" >  
    <circle cx="150" cy="150" r="100" fill="none" stroke="black" />  
</svg>     

• Загружаете этот файл в векторный редактор и выбираете в верхнем меню
  Контур / Оконтурить объект — Shift + Ctrl + C
  Сохраняете файл в формате SVG, копируете path

<svg xmlns="http://www.w3.org/2000/svg" viewBox="0 0 300 300">
  <path fill="none" stroke="black" stroke-width="2" d="M150 50C95 50 50 95 50 150 50 205 95 251 150 251 205 251 251 205 251 150 251 95 205 50 150 50zM150 51C205 51 250 95 250 150 250 205 205 250 150 250 95 250 51 205 51 150 51 95 95 51 150 51z"/>
</svg>

5

Никак не отрисовывается круг если в качестве конечной точки указать начальную. Но можно немного сместить)) В данном случае 60 —> 60.00001 и все работает. Можно одной дугой нарисовать круг.

Так как незамкнутая фигура все равно заливается, то результат почти идеальный, глазу не различимый точно. Возможные негативные последствия незамкнутого круга можно нивелировать инструкцией замыкания

z в конце строки пути. На отображение не повлияет, зато в векторных редакторах, наверняка, будет нормально заливаться цветом (без идеально замкнутого контура были бы ошибки заливки).

Для лучшего понимания отметил начало дуги (и почти конец ее же) красной точкой.

<svg xmlns="http://www.w3.org/2000/svg">
    <path d="M60 110 A 50 50 0 1 1 60.00001 110 z"
       stroke="black" fill="rgb(180,180,255)"/> 
    <circle cx="60" cy="110" r="3" fill="red"/>
</svg> 

Зарегистрируйтесь или войдите

Регистрация через Google

Регистрация через Facebook

Регистрация через почту

Отправить без регистрации

Почта

Необходима, но никому не показывается

Отправить без регистрации

Почта

Необходима, но никому не показывается

Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки

Как нарисовать звезду внутри круга — Блог о космосе

Пентакль (пентаграмма, вписанная в круг) — это символ, давно связанный с магией и оккультизмом, занимающий видное место в викке или современном колдовстве.

Поэтому начните с основных принципов рисования, отрабатывая геометрические фигуры и приемы света и тени, штриховки, обращая внимание на такие аспекты, как перспектива, пропорции, цвета и т. д. Овладение основами является ключевым для тех, кто хочет научиться рисовать и совершенствовать свои навыки рисования.

Звездчатый многоугольник — это сложный замкнутый многоугольник, у которого для любых трех последовательных произвольных сегментов два крайних сегмента лежат в одной и той же полуплоскости по отношению к среднему сегменту.

1. Интерпретация слева имеет 5 вершин правильного пятиугольника, поочередно соединенных, пропуская поочередные вершины. Внутренняя часть — это все, что находится непосредственно слева (или справа) от каждого ребра до следующего пересечения.

Эта семиконечная звезда может иметь разные значения, но все они связаны с идеей «священной вещи», такой как семь дней недели, семь планет в древних преданиях, семь магических металлов или семь столпы мудрости.

Это символ, связанный с сатанизмом, широко используемый средневековыми сатанистами как способ представления противоположности догм христианства.

Единственная звезда над девизом «Ordem e Progresso» представляет штат Пара. Это потому, что в 1889 году Пара была штатом, столица которого находилась севернее страны.

Основными символами этой политической теории являются черный флаг и буква «А» с кружком вокруг нее. Из двух символов наиболее известными являются «А», обозначающая слово «анархия», и круг (который на самом деле является буквой «О») и обозначающий слово «порядок».

Слово «пентаграмма» происходит от древнегреческого слова «звезда, состоящая из пяти точек». Пентаграмма — это фигура, которую можно построить одной линией, причем замкнутая переплетенная линия считается символом совершенства.

Пятиконечная звезда, также называемая пятиугольной звездой или пентаграммой, имеет пифагорейское происхождение и может быть построена с вершинами правильного пятиугольника, как показано на рисунке ниже. Следовательно, найдите сумму выделенных углов. m = S / n = [(n−2)180°] / n = [(5−2)180°] / 5 = 108°.

Для создания звезды вырежьте пять кусков одинаковой длины и примерно одинакового диаметра. Отрежьте первую и используйте ее, чтобы отметить длину оставшихся палочек. Для большего количества звезд, больше палочек.

Начните слегка, заштриховывая весь объект как можно более легкими штрихами. Продолжайте рисовать по всему рисунку, медленно заполняя более темные области, по одному оттенку за раз. Смешайте тени. Это лучший способ создать реалистичные плавные тени на любом рисунке.

Курс «Как рисовать все» научит вас лучшему способу научиться рисовать все, что вы хотите, просто и быстро, даже если вы не родились с «даром». Есть + 50 занятий, разделенных на 7 модулей с практическими и быстрыми упражнениями, которые через несколько дней смогут принести вам видимые результаты.

Интерпретация слева имеет 5 вершин правильного пятиугольника, поочередно соединенных, пропуская альтернативные вершины.

Пентаграмма (от древнегреческого πεντάγραμμος, пентаграмма) — звезда, состоящая из пяти прямых линий с пятью точками.

Звезды представляют собой большие сферы, образованные плазмой, нагретой до тысяч градусов. Его форма обусловлена ​​гравитацией, направленной на ядро ​​звезды. Звезды — это большие сферы плазмы, работающие за счет ядерного синтеза. Звезды — это большие сферы плазмы, удерживаемые вместе собственной гравитацией.

Самая яркая звезда — Альфа Центавра (или Альфа Центавра). Это самая близкая звезда к Земле, за исключением Солнца. В то время как последняя находится примерно в 150 миллионах километров от нашей планеты, Альфа Центавра находится от нас в сорока триллионах километров.

Это случай Умбанды, которая связывает каждую вершину треугольников с сущностью Умбанды. По словам масонского писателя Николы Аслана, Звезда Давида является визуальным представлением класса масонских символов, связанных с Богом, творением и совершенством.

ПЯТИКОНЕЧНАЯ ЗВЕЗДА: это мощный символ защиты и баланса. Каждая из его пяти точек представляет один из пяти проявленных элементов (Огонь, Воздух, Вода и Земля) плюс объединяющий элемент: Дух.

Рисование круга или эллипса

Макет

Совет: Вставленные файлы SketchUp теперь могут содержать пунктирные линии. Чтобы узнать больше об управлении этими новыми типами линий во вставленных файлах, см. раздел Работа с штрихами SketchUp в импортированных моделях

Хотите сделать документ LayOut более полным? Возможно, круг или эллипс могут помочь.

В LayOut есть инструмент «Круг» () и инструмент «Эллипс» (), которые можно найти в меню «Круги» на панели инструментов по умолчанию или в строке меню, выбрав Инструменты > Круги , а затем выберите нужный инструмент.

Вы можете нарисовать круг или эллипс визуально с помощью мыши или точно, введя координаты и значения в поле «Измерения». Когда вы рисуете круг или эллипс, помните о нескольких полезных советах:

• При необходимости вы можете переключаться между двумя методами (рисовать визуально или точно). Например, вы можете использовать мышь, чтобы разместить центральную точку круга, но использовать поле «Измерения», чтобы установить точный радиус или диаметр.
• Если вы допустили ошибку, нажмите клавишу Esc , чтобы начать заново.
• Абсолютные координаты относятся к верхнему левому углу области рисования. Например, чтобы ввести абсолютную координату, которая составляет 4 дюйма по оси X и 4,5 дюйма по оси Y, введите [4″, 4,5″] .

Подробную информацию о рисовании кругов и эллипсов, а также советы по специальным функциям этих инструментов см. в следующих разделах.

Содержание

1. Рисование круга
2. Рисование эллипса

Рисование круга

Чтобы нарисовать круг, выполните следующие действия:

1. Выберите инструмент Окружность ().
2. Щелкните, чтобы разместить центральную точку круга. Или введите абсолютные координаты в поле Измерения и нажмите Введите (Microsoft Windows) или Верните (Mac OS X).
3. Чтобы определить радиус круга, переместите курсор от центральной точки и нажмите, чтобы задать размер круга. Или введите значение радиуса или диаметра в единицах измерения. Например, для радиуса 5 дюймов введите
   5“ . Для диаметра 5 дюймов введите 5” d . (Если вы не укажете единицу измерения, LayOut использует единицы измерения по умолчанию, которые можно установить, выбрав Файл > Настройка документа и затем открыв панель Единицы.) Затем нажмите Ввод или Вернуть .

Совет: Нужна одна или несколько копий круга? Сразу после рисования круга дважды щелкните в области рисования, чтобы создать копию. Вы можете дважды щелкнуть, чтобы добавить столько копий, сколько вам нужно.

Рисование эллипса

Чтобы нарисовать эллипс, выполните следующие действия:

1. Выберите инструмент Эллипс ().
2. Чтобы разместить начальную точку эллипса, щелкните в области рисования. Или поместите начальную точку в точное место, введя абсолютные координаты в поле «Измерения».
3. Чтобы определить форму эллипса, переместите курсор от начальной точки. У вас также есть следующие варианты:
   • Чтобы превратить эллипс в круг, удерживайте нажатой кнопку Клавиша Shift .
   • Чтобы нарисовать эллипс из центра (вместо верхнего левого угла), удерживайте нажатой клавишу Ctrl (Microsoft Windows) или Option (Mac OS X).
   • Чтобы точно определить размер эллипса, введите абсолютные координаты конечной точки или введите размеры ширины и высоты. Расположение вашей мыши влияет на направление размеров. Например, чтобы нарисовать эллипс, который расширяется в нижний левый угол и имеет 4 дюйма в ширину и 3 дюйма в высоту, введите 4,3 и нажмите Введите или Верните . На следующем рисунке показан эллипс до ввода размеров (слева) и после (справа).
4. Если вы ввели точные размеры, все готово. Если вы используете мышь, нажмите, чтобы закончить эллипс.

Совет: Сразу после создания эллипса дважды щелкните в области рисования, чтобы создать точную копию. Вы можете дважды щелкнуть, чтобы сделать столько копий, сколько вам нужно.

• Круговой инструмент
• Диалоговое окно «Настройка документа»
• Инструмент «Эллипс»
• Макет
• Коробка для измерений

Проблема для размышления: 17 ноября 2011 г.

Ходить по кругу
Если мы возьмем любые две различные точки на окружности и соединим их хордой, хорда разделит внутреннюю часть окружности на две различные непересекающиеся области. Если мы возьмем три различные точки на окружности и соединим каждую пару из них хордой, мы можем образовать четыре различные точки. непересекающиеся области.

Какое максимальное количество непересекающихся областей можно образовать, выбрав четыре различные точки на окружности и соединив каждую пару из них хордой? Выбрав пять различных точек? Шесть различных точек? И, конечно же, n различных точек?

---

Некоторые размышления:   

Вспомним, что Ноябрьская задача для размышления была следующей: отдельные непересекающиеся участки. Если мы возьмем три различные точки на окружности и соединим каждую пару из них хордой, мы можем образовать четыре различные точки. непересекающиеся области.

Какое максимальное количество непересекающихся областей можно составить из хорд, соединяющих четыре различные точки на окружности? Пять различных точек? Шесть различных точек? n различных точек?

Эта проблема начинается довольно невинно. Мы можем видеть выше, что 2 области образованы 1 хордой, соединяющей 2 точки на окружности, и что 4 области образованы хордами, соединяющими 3 точки на окружности. Тогда мы можем заметить, что 8 областей могут быть образованы хордами, соединяющими 4 точки на окружности, и 16 областей могут быть образованы. хордами, соединяющими 5 точек на окружности — ах, как хорошо здесь живется! хороший 2 ^{n -1} образец, скажем, где n количество точек на окружности!

И тут наши надежды быстро рушатся, когда мы смотрим на корпус 6 очков.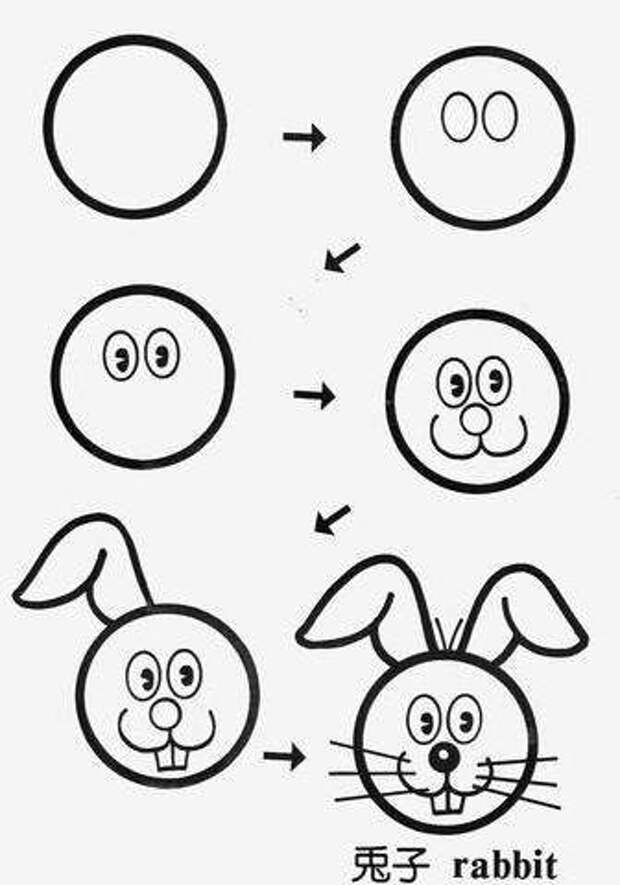

Паттерн «степени двойки» не работает, когда мы выбираем 6 точек на окружности. Максимальное количество областей, которые мы можем получить при пересечении хорд с 6 точками, равно 31. Учащиеся быстро понимают, что если 3 или более хорд пересекаются в одной и той же точке внутри круга, то они не получают максимально возможное количество регионов. Например, вершины 9Правильный шестиугольник 0133 на окружности создаст только 30 различных областей из его пересеченных хорд. Чтобы получить максимальное количество регионов, учащиеся должны разрешить пересечение не более 2 хорд. в той же точке.

Итак, это ваш подарок к математическому празднику — подумайте над этим еще немного!

---

Еще размышления:  

Вспомним, что Ноябрьская задача для размышления была следующей: отдельные непересекающиеся области. Если мы возьмем на окружности три различные точки и соединим каждую пару их хордой, мы получим четыре различных точки. непересекающиеся области.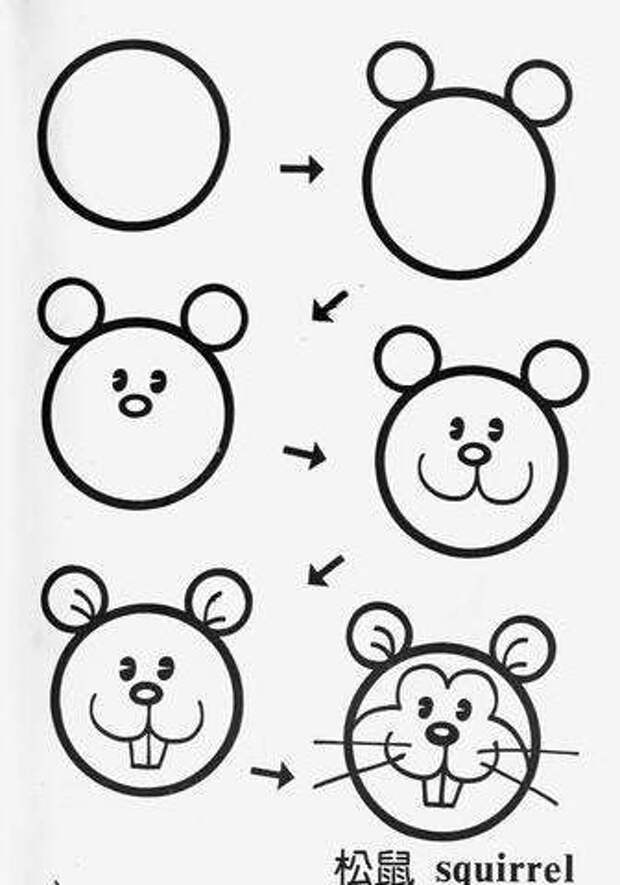

 

Какое максимальное количество непересекающихся областей можно составить из хорд, соединяющих четыре различные точки на окружности? Пять различных точек? Шесть различных точек? n различных точек?

В ходе размышлений в прошлом месяце мы обнаружили, что заманчивая схема удвоения для этой задачи исчезает при n = 6 точках. Мы обнаружили, что 8 областей образованы хордами, соединяющими 4 точки, и 16 областей образованы хордами, соединяющими 5 точек, но тогда 31 область образована хордами, соединяющими 6 точек!

Сколько областей можно образовать хордами, соединяющими 7 точек на окружности?

Существуют различные способы поиска закономерностей или подсчета областей при выборе дополнительных точек на окружности. Давайте рассмотрим один подход, который я видел у студентов.

В последовательности диаграмм, показанных ниже для семи точек, мы замечаем, что новая подобласть образуется в круге каждый раз, когда хорда встречается с вершиной и каждый раз, когда хорда пересекает другую хорду.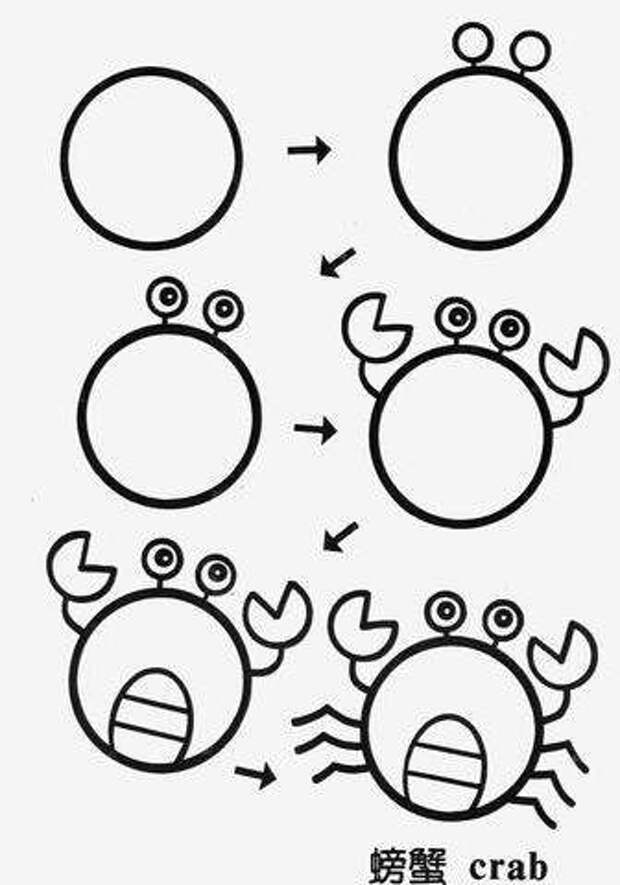 Сначала формируют 7 областей, строя все хорды с точкой A как вершина.

Далее формируются дополнительные (1 + 2 + 3 + 4 + 5) или 15 областей путем построения всех новых хорд из точки B (см. ниже). Сегмент BC образует область 8, сегмент BD образует области 9 и 10, сегмент BE образует области 11, 12, 13 и так далее. Каждый раз, когда хорда пересекает ранее построенную хорду, она добавляет еще одну область, что также происходит каждый раз, когда хорда встречается с вершиной, поскольку предыдущие области разбиваются на две части каждый раз, когда хорда пересекает другую хорду или встречается с вершиной.

Когда мы добавляем новые хорды из вершины C , CD образует 1 новую область, CE образует 3 новых области, CF образует 5 новых областей, а CG формирует 7 новых областей, потому что эти аккорды пересекают 0, 2, 4 и 6 предыдущих аккордов соответственно. Таким образом, мы формируем дополнительные 1 + 3 + 5 + 7 или 16 новых регионов.

Схема дополнительных областей, образованных хордами из вершины D , следующая:  DE формирует 1, DF формирует 4 и DG формирует 7 новых областей, что дает нам 1 + 4 + 7 или 12 новых областей.

Для хорд из вершины E , EF образует 1 новую область, а EG образует 5 новых областей, так как он пересекает 4 хорды и затем встречается с вершиной G , что дает 1 + 5 или 6 , новые регионы.

И, наконец, хорда FG образует 1 дополнительную область. Итак, всего у нас 7 + (1+2+3+4+5) + (1+3+5+7) + (1+4+7) + (1+5) + 1, или 57, образовавшихся областей хордами, соединяющими 7 точек. Наш паттерн явно нелинейный, не так ли! Прекрасный!

Учитывая типы узоров, которые мы видим выше, мы можем предположить, что если выбрать 8 точек на окружности и соединить их хордами, получится 8 + (1+2+3+4+5+6) + (1+3+ 5+7+9) + (1+4+7+10) + (1+5+9) + (1+6) + 1 или 99 областей.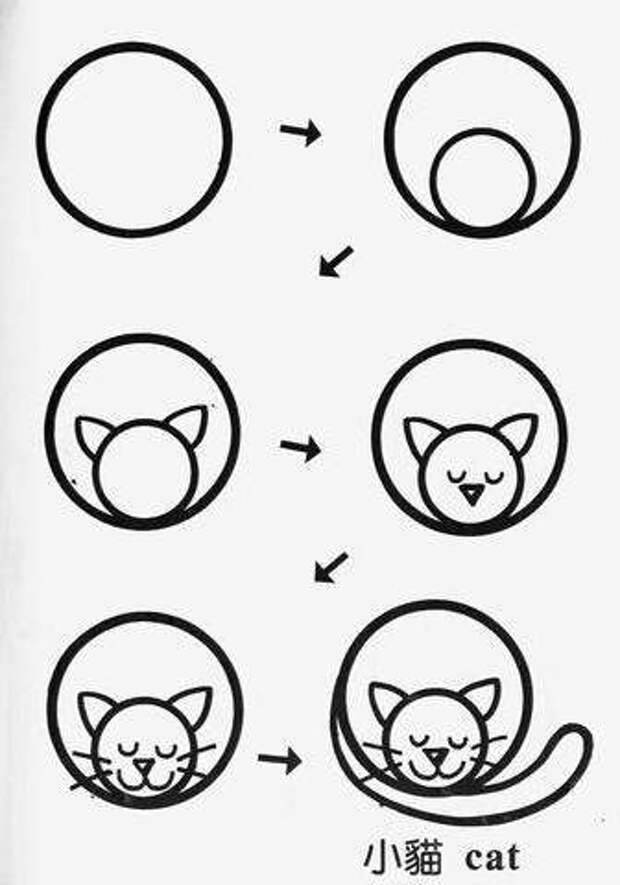

Если мы вернемся к более ранней задаче для размышления «Вычисление фигурных чисел» (сентябрь 2011 г.), то заметим, что приведенный выше паттерн также является суммой фигурных чисел. Например, количество областей, образованных хордами, соединяющими 8 точек на окружности, равно: 

     8  (количество точек)

+ 21 (6-е треугольное число)

+ 25 (5-е квадратное число)

+ 22 (4-е пятиугольное число)

+ 15 (3-е 00-угольное число)

+  7  (второе семиугольное число)

 + 1  (первое восьмиугольное число)

Ваши ученики могут найти множество других способов выявления закономерностей в этой задаче. Следующий вопрос: можем ли мы найти формулу замкнутой формы, которая даст нам количество областей, образованных хордами, соединяющими n точки? То есть можем ли мы выразить число областей в окружности как функция n , числа точек на ней, соединенных хордами?

Если функция является полиномиальной функцией от n , то метод конечных разностей последовательности последовательных членов может подсказать нам, какой будет степень этого полинома.